关于摩擦力做功的结论在解题中的应用

(江苏省奔牛高级中学，江苏 常州 213131)

1 结论的由来

在应用动能定理解题时，我们会碰到如下问题：

例题1 如图1所示，一个物体从斜面上高h处由静止滑下，紧接着在水平面上滑行一段距离后停止，量得停止处相对开始运动处的水平距离为s，不考虑物体滑至斜面底端的碰撞作用，并认为斜面和水平面对物体的动摩擦因数相同，求动摩擦因数μ.

图1

图2

2 对结论的理解

物体在如图1所示的全程中滑动摩擦力所做的功，从效果上看，相当于物体在长为s的水平面上运动过程中滑动摩擦力所做的功，即可将图2全程中滑动摩擦力所做的功等效成物体在水平面上运动相同水平位移时滑动摩擦力所做的功.只要全程所对应的水平位移相同，则全程滑动摩擦力所做的功相同.

此结论适用于物体在垂直于接触面方向上只受支持力和重力(或垂直于接触面方向的重力的分力)，若物体在平行于接触面方向上除摩擦力外还受其它力作用，结论仍然成立.

3 结论的应用

(1)简单应用

例题2 如图3所示，OD是一水平面，AB为一斜面，一质点由A点静止释放，沿斜面AB滑下，最后停在D点，不考虑物体滑至斜面底端的碰撞作用，若斜面改为AC(仅倾角变化)，仍从A点由静止释放，设斜面与水平面对物体的动摩擦因数相同，则最终停在水平面OD上的( ).

A.D点右侧 B.D点左侧

C.D点 D.无法确定

解析：设A点竖直高度为h，质点从斜面AB由静止滑下停在D点，对应水平位移为s1，则根据动能定理和wf=-μmgs这一结论可得mgh-μmgs1=0，若质点从斜面AC由静止滑下至最终停止，设对应水平位移为s2，则有mgh-μmgs2=0，比较两个方程可知s1=s2，即质点最终仍然停在水平面上的D点，正确选项为C.

(2)综合应用

例题3 水上滑梯可简化成如图4所示的模型：倾角为θ=37°斜滑道AB和水平滑道BC平滑连接，起点A距水面的高度H=7.0m，BC长d=2.0m，端点C距水面的高度h=1.0m. 一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.10．(取重力加速度g=10m/s2，cos37°=0.8，sin37°=0.6.)

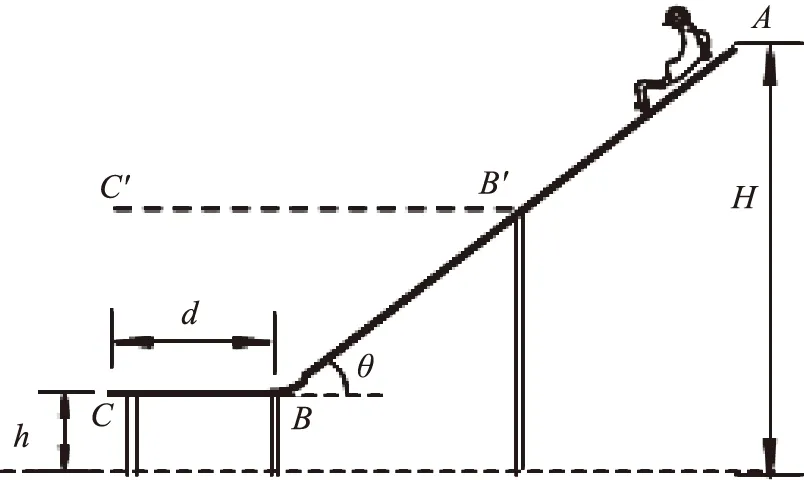
图4

①求运动员沿AB下滑时加速度a的大小；

②求运动员从A滑到C的过程中克服摩擦力所做的功W和到达C点时速度v的大小；

③保持水平滑道端点在同一竖直线上，调节水平滑道高度h和长度d到图中B′C′位置时，运动员从滑梯平抛到水面的水平位移最大，求此时滑道B′C′距水面的高度h′.

解析：①由牛顿第二定律F=ma得a=gsinθ-μcosθ=5.2m/s2.

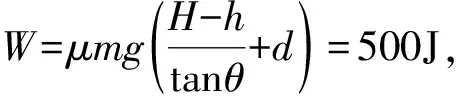
(3)拓展提高

例题4 如图5所示，一个滑雪运动员从左侧斜坡距离坡底竖直高度H1=8m的高处由静止自由滑下，以坡底为零势能参考面，当下滑到距离坡底h1高处时，运动员的动能和势能恰好相等，到坡底后运动员又冲上右侧斜坡，当上滑到距离坡底h2高处时，运动员的动能和势能再次相等，最后上滑的最大高度H2=4m，全程运动员通过的水平距离为s=20m，运动员与斜坡间的动摩擦因数处处相等，不计经过坡底时的机械能损失.在此过程中，下列说法正确的是( ).

图5

A.h1<4m,h2>2m

B.滑雪板与雪面的动摩擦因数为0.2

C.滑雪运动员到达右侧最高处后可能不再返回

D.滑雪运动员从右侧返回再次冲上左侧斜坡的最大高度为2m

解析：下滑过程中有机械能损失，所以有mgH1>2mgh1，可得h1<4m；同理可得h2>2m，则A正确.

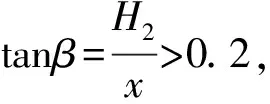
图6

将H3=2m代入公式，求得S′=10m，并求得tanα=0.6，可知tanβ=0.6，可见，只有满足两坡道倾角相等时，故D选项正确.

在高中物理中经常会出现涉及斜面与平面相结合的题目，而且往往会涉及到滑动摩擦力做功，如果能灵活应用Wf=-μmgs这一结论，无疑可以拓宽解题思路，简化解题过程，提高解题速度.