泵用不可压缩流体密封刚度系数分析

张盟，王晓放，徐胜利，万学丽

(1.大连理工大学 能源与动力学院，辽宁大连116023;2.大连深蓝泵业有限公司，辽宁 大连116031)

泵叶轮入口轮盖与进口导流管间存在动静间隙。部分高压流体经叶轮出口间隙外泄，并重新回流至泵入口，这股回流既消耗主泵的功率，也干扰主流场流动，同时减小有效通流面积，降低泵的流动效率和性能。为了尽量降低这种泄漏，在动静间隙上设置非接触式不可压缩流体密封。

非接触式密封技术广泛应用在泵等旋转机械中，它能够有效控制旋转部件与静止部件间的泄漏。对于转子动力系统，密封会提供附加的刚度和阻尼，这对转子的稳定性造成一定的影响［1］。

Childs等［2-4］对控制体方法不断改进。Arghir等［5-7］发展了 CFD方法，并计算动力特性系数。Benckert等［8］做了大量的关于动力特性的实验，并证明密封的交叉刚度是由密封周向流动引起的，他们在实验中测量了不同类型密封的直接刚度，发现较长密封的直接刚度为负值。Leong等［9］蒸汽轮机迷宫密封做了大量试验，结果与Benckert等的测量结果很吻合，多数密封直接刚度为负，少量短密封为正。Mihai等［10］发现进出口压差较小时，出口有回堵现象，动力特性系数中的直接刚度系数出现负值，影响转子的对中效应，转子稳定性差。

国内何立东等［11-13］用实验和数值方法研究动力特性系数。模拟仿真方面，孙婷梅等［14-15］利用CFD有限元软件Fluent计算迷宫密封三维流场，研究了偏心率、入口预旋、涡动速度对密封动力特性的影响，密封直接刚度维持在负值范围，他们计算出密封周向压力分布曲线，但是没有分析产生负直接刚度的原因。

本文应用数值模拟结合工程实际，利用CFD有限元软件Fluent计算LNG泵的节流衬套和口环密封的动力特性系数，模拟在LNG泵不同转速工况下，不可压缩流体密封的动特性变化，通过分析比较密封圆周上压力和速度分布，研究等截面环形密封产生负直接刚度的原因和影响因素。

1 密封模型

1.1 涡动转子数学模型

本文假设整体计算域为湍流，湍流模型采用标准的k-ε模型［16］，近壁面采用标准壁面函数:

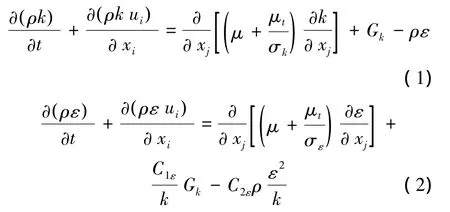
式中:Gk表示由平均速度梯度产生的湍动能项，Gb表示由浮力产生的湍动能项，YM表示由可压缩湍流中，耗散率的波动项，方程常数项C1ε=1.44，C2ε=1.92，Cμ=0.09，还有 σk=1.0，σε=1.3 分别是湍动能k和湍动能耗散率ε的湍流普朗特数，Sk和Sε是自定义源项，标准k-ε湍流模型是半经验公式。

1.2 涡动转子动力学模型

本文采用旋转坐标系，在转子中心定义坐标系，转子与静子的相对位置不变，坐标系变换把非定常问题转换成定常问题。图1所示偏心转子在静子中涡动受力，e为转子偏心距，本文假设转子绕静子中心以圆形轨迹涡动，涡动半径是转子偏心距e，涡动角速度是Ω，转子的旋转角速度是ω，转子的旋转角速度与涡动角速度比值定义为涡动比，涡动轨迹的径向力和切向力为Fr、Ft。

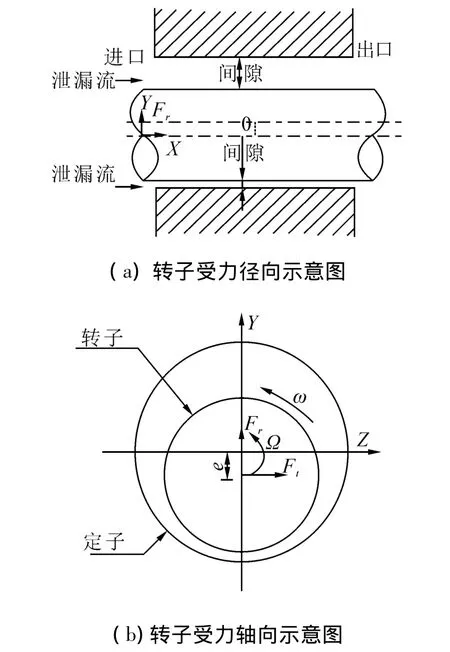
图1 偏心转子在静子中涡动受力示意图Fig.1 Force on eccentric rotor in stator

1.3 动力学方程

当转子受到小扰动，以小圆形轨迹绕静子中心涡动，转子受到的水动力可以由刚度、阻尼和惯性系数的反对称矩阵和转子的位移、速度、加速度的线性关系表示，矩阵中包括 6个独立参数(K，k，C，c，M，m)，K为直接刚度，k为交叉刚度，C为主阻尼，c为交叉阻尼，M为主惯性系数，m为耦合惯性系数。

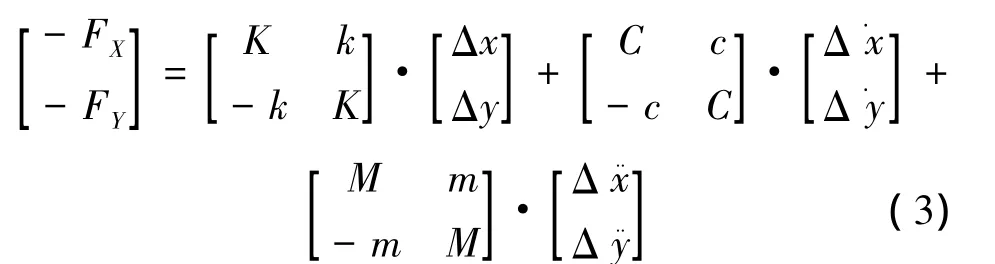
在不同的涡动比下，积分转子表面压力生成转子涡动轨迹的径向力和切向力Fr、Ft，径向力和切向力的二阶方程:

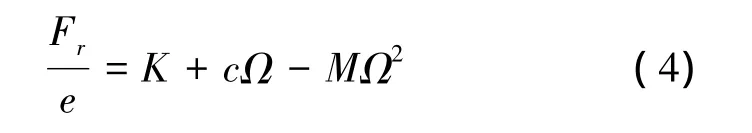
本文求解密封线性动力特性，偏心距选取径向间隙的10%，Moore等［17］验证过此值在模拟小轨迹涡动的准确性。

为了求解特性系数，至少选取3个涡动比，为了提高计算精度，一般选取6个涡动比，对结果进行线性回归计算。

1.4 计算域和边界条件

图1(b)所示转子和静子相对位置的轴向视图，在计算域入口指定总压，出口指定静压。旋转坐标系下，转子壁面相对角速度为ω-Ω，密封壁面相对角速度为-Ω。给定湍流强度和水力直径。在转子和密封壁面为标准壁面条件，采用速度无滑移条件，流动绝热。

1.5 求解方法

求解器选择分离的隐式求解器，采用有限体积法离散控制方程。连续方程、动量方程和能量方程的离散格式为二阶迎风格式，湍动能和耗散率方程采用一阶迎风格式。

1.6 网格

在偏心状态下生成三维结构化六面体网格，偏心距选取间隙的10%。图2为槽道式密封间隙和槽道二维网格。为了提高求解精度，在近壁面增加了网格密度，相邻两节点间距离之比为1.1。Hirano等［7］验证了密封空腔和间隙网格密度独立性，证明了本文网格密度计算结果的可靠性。

图2 槽道式密封间隙和槽道二维网格Fig.2 Mesh of land and groove for grooved seal

2 计算结果与分析

2.1 等截面环形密封数值模拟

图1(a)为等截面环形密封示意图，对不同间隙等截面环形密封的不同转速工况进行数值模拟，转速nr=500～10 000 r/min，额定转速n=2 980 r/min，模拟介质为液态LNG，其他参数为:内径Di=53.2 mm，外径Do=53.5 mm，密封长度L=50 mm，L/Di=0.94(长密封)，介质进出口压差 ΔP=0.005 MPa，环境压力P0=0.1MPa，动力粘度 μ=0.000 125 kg/(m·s)。

计算1 000～10 000 r/min转速工况下，1倍间隙和2倍间隙(磨损)等截面环形密封刚度特性系数，分析转速对刚度特性系数的影响，如图3所示，等截面环形密封直接刚度为负值，1倍间隙直接刚度的绝对值大于2倍间隙的绝对值，且直接刚度的绝对值随着转速的增大而增大，1倍间隙的增大幅度比2倍间隙大。1倍间隙的交叉刚度大于2倍间隙的交叉刚度。转速增大时，交叉刚度增大，且1倍交叉刚度的增幅大于2倍交叉刚度。

如图4所示，在5 000r/min工况下，等截面环形密封最大间隙和最小间隙的速度和压力特性曲线，等截面环形密封介质压力沿轴向下降，斜率和速度有关。密封周向间隙不均匀，介质受高速旋转的转子的摩擦力影响，在最小间隙处形成较最大间隙更大的周向速度，因此在最小间隙处形成较最大间隙处更大的速度。如图4(a)在密封进口处，最大间隙和最小间隙的速度激增，且最小间隙的加速度大于最大间隙，这部分动能增量消耗更多压力能，如图4(b)密封进口处，最小间隙压力下降幅度明显大于最大间隙;在密封中部，速度基本保持定值，最大间隙和最小间隙压降斜率一致;在接近密封出口，最大间隙处压力急剧下降，最小间隙处缓慢下降，同时下降到出口压力，在此过程最大间隙和最小间隙的速度相应幅度的增长。在密封轴向长度上，最小间隙处压力始终小于最大间隙处，因此表明直接刚度为负值，且直接刚度系数与压力特性曲线包含的面积有关。

图3 等截面环形密封刚度特性曲线Fig.3 Stiffness characteristic of annular seal

如图5(a)所示，在极坐标系下，在2 950 r/min工况下，1倍间隙和2倍间隙等截面环形密封2/5轴长处，圆周上各角度速度，介质在密封环内成螺旋轨迹流动，在圆周方向上最小间隙受到最大流动阻力，产生节流效应，1倍间隙密封在270°位置(最小间隙)速度达到最大，如图5(b)在174°位置压力最大，在334°压力最小，因此以 174°、334°为分界点，从174°到334°在转速方向上提供较大的压力势，促进介质加速流动;然而从334°到174°转速方向上提供反向压力势阻止介质流动，在88°位置速度最低。在同样的压差边界条件下，2倍间隙泄漏大于1倍间隙，因此各角度速度大于1倍间隙。

图4 等截面环形密封(5 000 r/min)最大间隙和最小间隙的速度和压力特性曲线Fig.4 Velocity and pressure of annular seal maximum and minimum clearance in the condition of 5 000 r/min

图5(b)中，压力特性椭圆中心向上偏离，表征密封产生负直接刚度;向左偏离，表征产生正交叉刚度;偏离极坐标系中心越大，表征刚度值越大。1倍间隙密封在较窄的流道内受到较大的阻力，所以压力特性椭圆中心偏心较大，1倍间隙的交叉刚度大于2倍间隙，直接刚度绝对值稍大于2倍间隙。因此，密封从正常间隙磨损成2倍间隙可以减小负直接刚度的不稳定影响。

图6所示等截面环形密封不同转速圆周压力分布对比图，如图6(a)，随转速增大，压力特性椭圆中心向左上方偏离距离逐渐增大，表征负直接刚度和交叉刚度的绝对值逐渐增大，稳定性下降。

如图6(b)，不同转速下压力特性点对比图，特性点包含的面积与直接刚度的绝对值成正比，压力特性点面积的长轴线斜率的绝对值与交叉刚度的绝对值成正比。随着转速增大，直接刚度的绝对值逐渐增大，交叉刚度逐渐增大。10 000 r/min工况下负直接刚度绝对值最大，1 000 r/min工况下负直接刚度绝对值最小;10 000 r/min工况下正交叉刚度最大，1 000 r/min工况下正交叉刚度最小。

如图6(c)，1 000 r/min和500 r/min压力特性点对比图，1 000 r/min压力特性点出现交叉点，500 r/min压力特性交叉点向z轴正方向移动，直接刚度由负值变为正值。因此，推测随着转速的继续降低，直接刚度会逐渐增大。推论高转速是造成负刚度现象的因素之一。

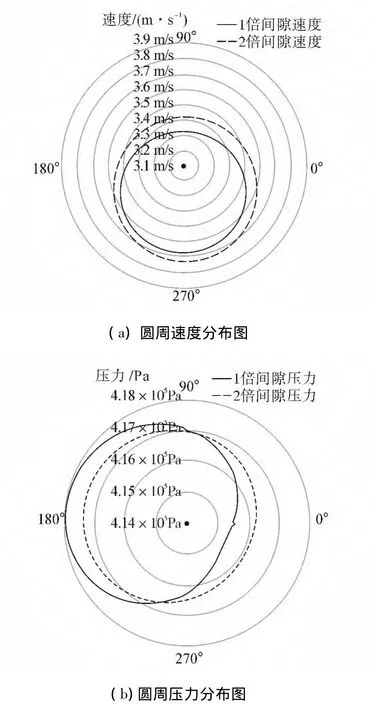
图5 等截面环形密封(2 950 r/min)1倍间隙和2倍间隙的速度和压力特性椭圆Fig.5 Velocity and pressure circumferential distribution of annular seal normal clearance and twice clearance in the condition of 2 950 r/min

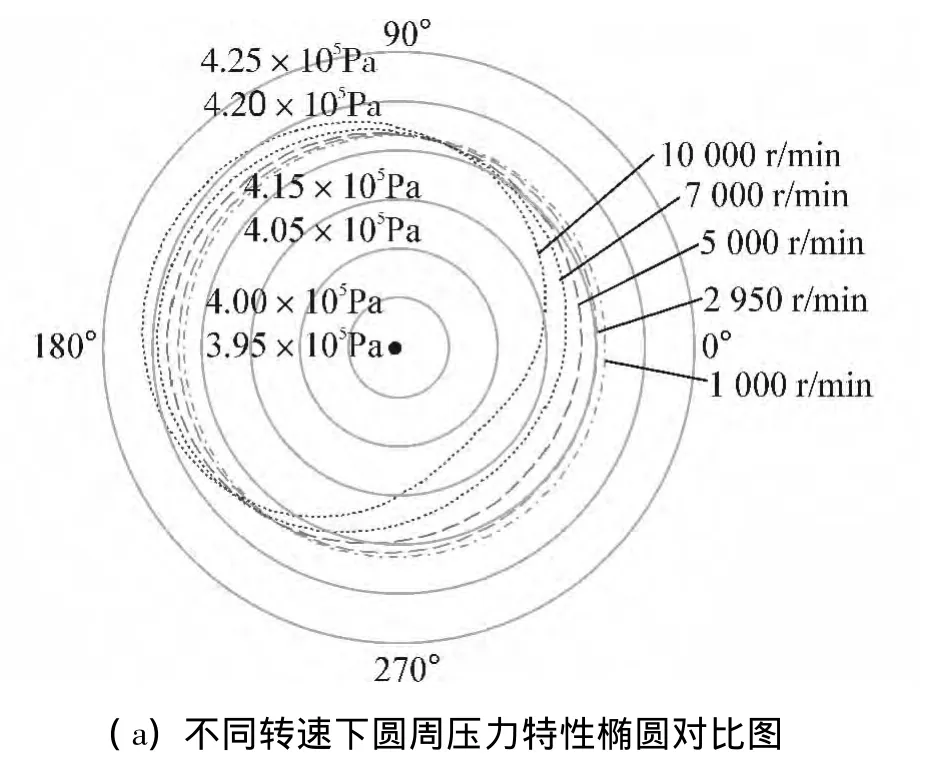
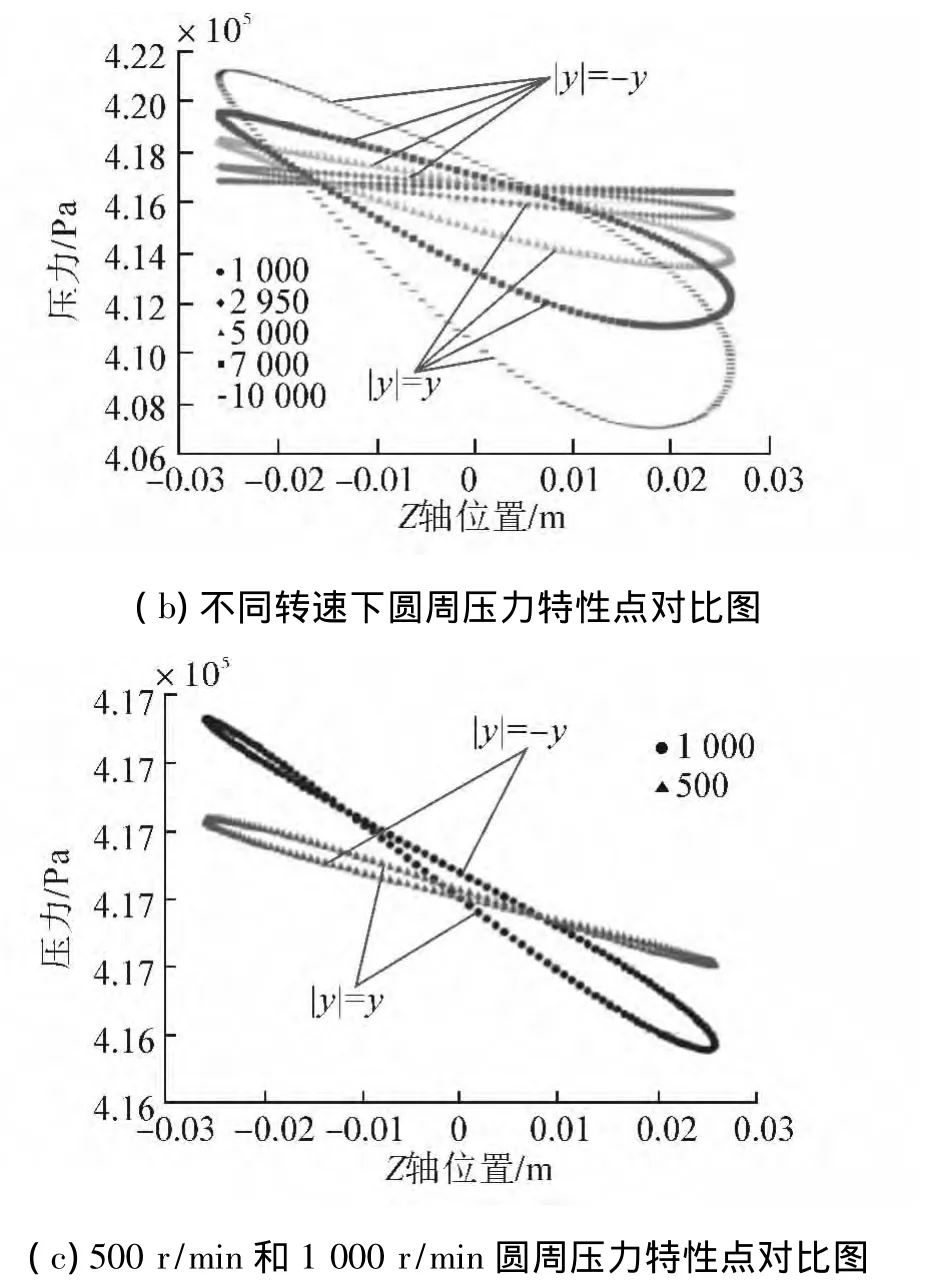
图6 等截面环形密封不同转速圆周压力分布对比图Fig.6 Comparison of pressure distribution for annular seal over a range of rotating speed

2.2 槽道式密封数值模拟

图7为槽道式密封示意图，对槽道式密封的不同转速工况进行数值模拟，转速nr=1 000～7 000 r/min，额定转速n=2 980 r/min，模拟介质为液态LNG，其他参数为:内径Di=194.65 mm，外径Do=195.05 mm，密封长度L=28.5 mm，槽道数量N=6，槽道深度h=2 mm，槽道宽度w=2 mm，介质进出口压差 ΔP=0.37 MPa，环境压力P0=0.1 MPa，动力粘度 μ=0.000 125 kg/m·s。

计算在1 000～10 000r/min转速工况下，1倍间隙和2倍间隙(磨损)槽道式密封刚度特性系数，分析转速对刚度特性系数的影响，如图8所示，槽道式密封1倍间隙直接刚度小于2倍间隙直接刚度，且直接刚度随着转速呈现缓慢下降的趋势。1倍间隙的交叉刚度大于2倍间隙的交叉刚度。转速增大时，交叉刚度增大，且1倍交叉刚度的增幅大于2倍交叉刚度。

图9所示槽道式密封圆周压力特性点对比图，由于槽道式密封有较大密封腔室，所以密封圆周压力和速度分布比等截面环形密封更均匀，最大间隙和最小间隙之间压差较等截面环形密封更小，更不会出现最小间隙压力比最大间隙小的现象。在相同压差边界条件下，2倍间隙槽道式密封的泄漏量较1倍间隙大，速度也较大，因此压力较1倍间隙小。对于槽道式密封圆周平均压力越小，压力特性点包含的面积越大，槽道式密封直接刚度越大。2倍间隙槽道式密封的直接刚度大于1倍间隙，交叉刚度小于1倍间隙。

图10所示为2倍间隙槽道式密封不同转速下压力特性点对比图。对于较大间隙槽道式密封，随着转速增大，圆周平均压力值逐渐增大，且趋于均匀，压力特性点包含的面积逐渐缩小，直接刚度逐渐减小，交叉刚度逐渐增大，但增大幅度较小。1 000 r/min工况下直接刚度最大，7 000 r/min工况下直接刚度最小。7 000 r/min工况下交叉刚度最大，1 000 r/min工况下交叉刚度最小。

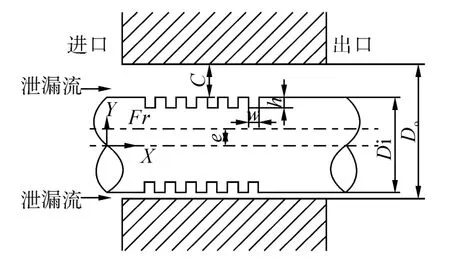
图7 槽道式密封示意图Fig.7 Grooved seal

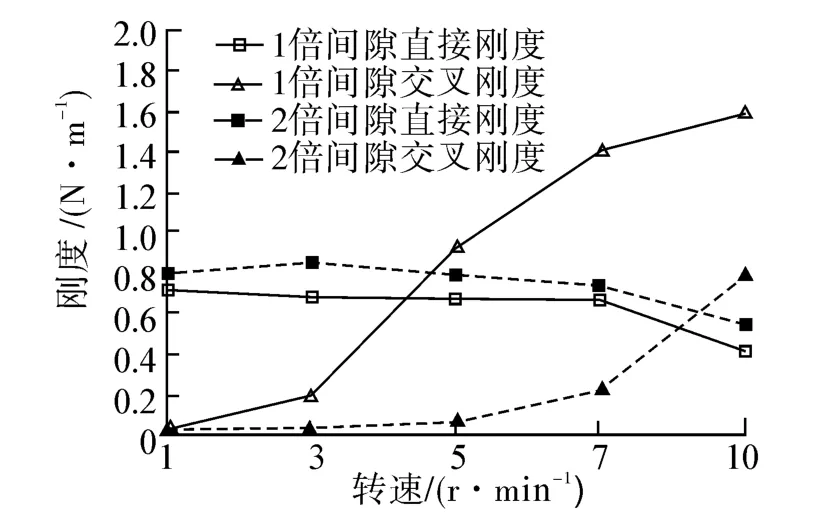
图8 槽道式密封刚度特性曲线Fig.8 Stiffness characteristic of grooved seal

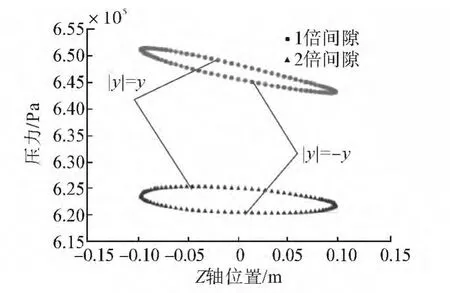
图9 槽道式密封(7 000 r/min)圆周压力特性点对比图Fig.9 Pressure change with Z-coordinate for grooved seal at 7 000 r/min

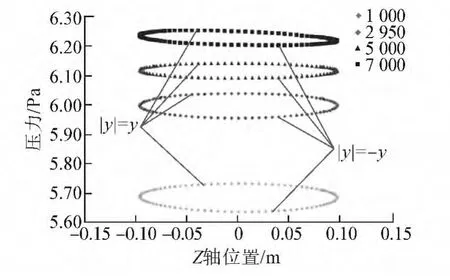
图10 槽道式密封不同转速圆周压力特性点对比图Fig.10 Pressure change with Z-coordinate for grooved seal over a range of rotating speed

3 结论

1)等截面环形密封和槽道式密封的1倍间隙直接刚度小于2倍间隙，1倍间隙交叉刚度大于2倍间隙，密封经过磨损泄漏量增大，稳定性却提高。

2)转速使等截面环形密封和槽道式密封的直接刚度下降，交叉刚度增大，造成稳定性下降，且随转速不稳定隐患成倍增长。

3)对于不可压缩流体，较长的等截面环形密封容易产生负直接刚度，槽道式密封直接刚度通常为正值，比等截面环形密封更加稳定，工程上建议采用槽道式密封控制不可压缩流体泄漏。

4)对于等截面环形密封，高转速容易造成负刚度现象的重要因素，但对于旋转机械，为避免这种现象，工程上建议增大间隙以减小转子不稳定隐患。

影响负刚度的因素很多，在结构参数上，密封的L/D比值是产生负刚度的重要的结构参数，本文计算的等截面环形密封L/Di=0.94属于长密封，容易产生负刚度且与短密封动特性有很大差别。针对长密封的结构参数对动特性影响还有待于进一步研究。

［1］BLACK H F，COCHRANE E A.Leakage and hybrid bearing properties of serrated seals in centrifugal pumps［C］//The 6th International Conference on Fluid Sealing.Munich，Germany，1973:G5-61-G5-70.

［2］CHILDS D W，SCHARRER J K.An Iwatsubo based solution for labyrinth seals:a comparison to experimental results［J］.ASME J Eng Gas Turbines Power，1986，108:325–331.

［3］IWATSUBO T，SHENG B.Evaluation of dynamic characteristics of parallel grooved seals by theory and experiment［C］//Proceedings of the Third IFToMM International Conference on Rotordynamics.Lyon，France，1990:313-318.

［4］FLORJANCIC S.Annular seals of high energy centrifugal pumps:a new theory and full scale measurement of rotordynamic coefficients and hydraulic friction factors［D］.Zurich:Swiss Federal Institute of Technology，1990:26-63.

［5］ARGHIR M，FRENE J.Rotordynamic coefficients of circumferentially-grooved liquid seals using the averaged Navier-Stokes equations［J］.ASME J Tribology，1997，119:556-567.

［6］MOORE J J.Three-dimensional CFD rotordynamic analysis of gas labyrinth seal［J］.ASME Journal of Vibrations and Acoustics，2003，125:427-433.

［7］HIRANO T，GUR Z，KIRK R G.Application of computational fluid dynamics analysis for rotating machinery-part II:labyrinth seal analysis［J］.ASME J Eng Gas Turbines Power，2005，127:820-826.

［8］BENEKERT H，WACHTER J.Flow induced spring coefficients of labyrinth seals for applications in turbomachinery［C］//Rotordynamic Instability Problems in High-Performance Turbomachinery.Texas:NASA，1980:189-212.

［9］LEONG Y，BROWN R D.Circumferential pressure distributions in a model labyrinth seal［C］//Rotordynamic Instability Problems in High-Performance Turbomachinery.Texas:NASA，1982:223-241.

［10］MIHAI A，CYRIL D，JEAN F.The Lomakin effect in annular gas seals under choked flow conditions［J］.ASME Journal of Tribology，2007，129(4):1028-1034 .

［11］何立东，高金吉，金琰，等.三维转子密封系统气流激振的研究［J］.机械工程学报，2003，39(3):100-104.HE Lidong，GAO Jinji，JIN Yan，et al.Study on gas flow-induced vibration for a three-dimensional rotor-seal system［J］.Chinese Journal of Mechanical Engineering，2003，39(3):100-104.

［12］王炜哲，刘应征，叶春，等.迷宫密封-转子系统动力学特性的试验测量和数值模拟［J］.机械工程学报，2007，43(3):22-27.WANG Weizhe，LIU Yingzheng，YE Chun，et al.Experimental measurement and numerical simulation of dynamics of labyrinth seal—rotor combination［J］.Chinese Journal of Mechanical Engineering，2007，43(3):22-27.

［13］曹浩，杨建刚，郭瑞，等.密封动力特性系数试验识别方法及影响因素分析［J］.机械工程学报，2011，47(9):85-89.CAO Hao，YANG Jiangang，GUO Rui，et al.Experimental identification method and influence factor analysis of seal dynamic characteristic［J］.Chinese Journal of Mechanical Engineering，2011，47(9):85-89.

［14］孙婷梅，郑水英.基于FLUENT迷宫密封动力特性分［J］.流体机械，2008，136(108):24-28.SUN Tingmei，ZHENG Shuiying.Dynamic coefficient analysis of labyrinth seal based on FLUENT［J］.Fluid Machinery，2008，136(108):24-28.

［15］孙婷梅.迷宫密封流场及其动力特性计算［D］.杭州:浙江大学，2008:30-48.SUN Tingmei.Flow and dynamic coefficients of labyrinth seals［D］.Hangzhou:Zhejiang University，2008.

［16］LAUNDER B E，SPALDING D B.Lectures in mathematical models of turbulence［M］.London:Academic Press，1972:32-126.

［17］MOORE J J，PALAZZOLO A B.CFD comparison to 3D laser anemometer and rotordynamic force measurements for grooved liquid annular seals［J］.Journal of Tribology-transactions of The ASME，1999，121(2):307-314.