无人水下航行器近海底空间路径规划方法

严浙平，邓超，赵玉飞，李本银

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

近年来无人水下航行器 (unmanned underwater vehicle，UUV)作为海洋探测与开发的有力工具越来越受到人们的重视。UUV路径规划作为保障UUV安全、高效完成作业任务的重要功能，具有重要的现实意义。国内外众多学者在这方面进行了大量研究，提出了很多有效规划算法，取得了丰富的研究成果，如人工势场、A*算法、可视图法、快速扩展随机数、Voronoi图以及各种优化算法等获得了广泛的研究与应用［1-5］。然而，在一些特殊的侦查和探测任务中，UUV在回避障碍威胁的同时，还需要实现对地形的跟随。在这种情况下，不能使用单纯朝向目标的规划方法，而要对地形威胁进行约束，使UUV在保证安全的情况下，实现近海底航行。

优化算法本身具有较强的寻优能力，而路径规划更多的是需要得到一个较优化的路径，因此，将优化算法用于路径规划问题是研究的一个重要方面。作为仿生智能优化算法的一种，粒子群优化算法(particle swarm optimization，PSO)，具有概念简单、参数调节方便、较强的寻优能力等特点，一经提出便受到了广泛的关注［6-8］。本文考虑地形威胁约束，结合UUV自身性能，计算UUV近海底航行安全深度。将UUV近海底航行安全深度作为UUV航行深度，提出UUV躲避障碍和趋近目标代价函数，最终得到UUV近海底航行路径规划代价函数。提出一种改进的粒子群算法，将其用于路径规划代价函数寻优，以实现UUV近海底航行路径规划。

1 UUV近海底航行安全深度

由于海底地形起伏分布有着很大的差异，再加上UUV航行性能和航行速度的不同，在UUV穿越区域内不同方向，UUV安全航行深度有所不同。这就需要计算UUV当前点航行方向上的最大安全深度。假设UUV当前路径点为P点，计算UUV路径点P的安全深度，围绕P点沿着UUV前进方向，向外扩展一定区域，如图1所示，通过计算该区域的安全度，得到P的安全深度。首先将采样计算区域网格化，然后计算网格点的均方差δ，利用均方差δ表达地形的起伏度，从而确定UUV的安全航行深度。

图1 安全深度采样计算区域Fig.1 Sampling calculation of safety depth area

则UUV最小离地高度为

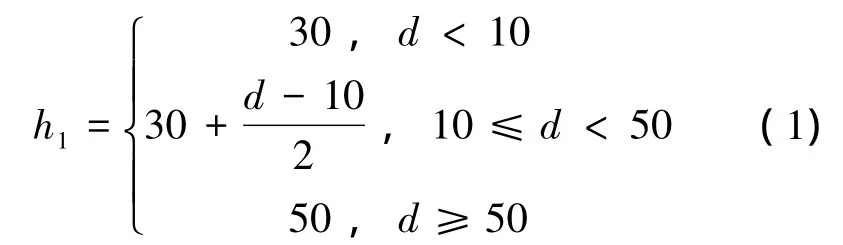
UUV航行时受自身机动性能限制，需要满足纵倾角与纵倾角速度约束，取纵倾角θ，最大纵倾角θmax，纵倾角速度q，最大纵倾角速度qmax则有

图2所示，为纵倾角约束下最小离地高度示意图，路径点在采样计算区域中，UUV纵倾角约束下UUV最小离地高度h2为使最大仰艏前行曲线在采样计算区域中海底地形上方30 m的路径点高度。

受水密性、材料、耐压性能的影响，UUV具有一定的下潜深度约束Dmax，若P点垂面内海洋深度为Hp，则下潜深度约束下最小离地高度为

综合以上约束，得到UUV近海底航行路径点最小离地高度为

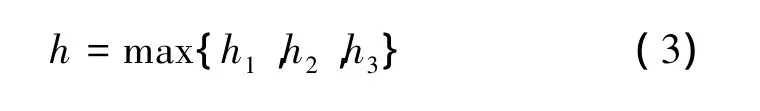
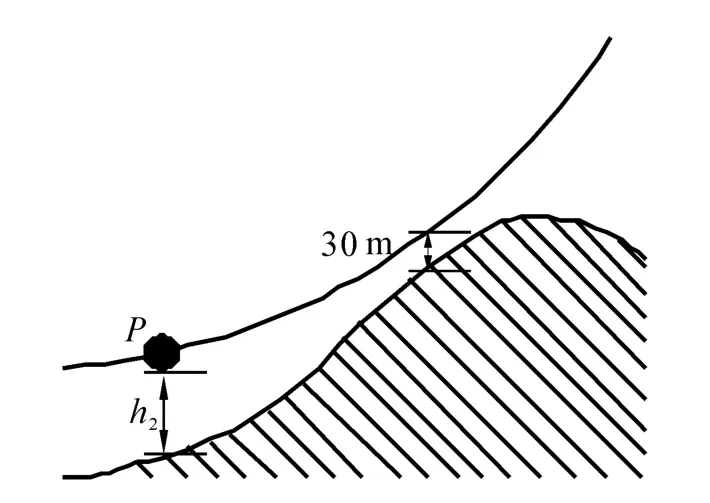
图2 纵倾角约束下最小离地高度示意图Fig.2 Pitch angle constraints under the minimum height

2 UUV路径规划方法

UUV规划起始点坐标为P0(x0，y0，z0)，路径点坐标为pi(xi，yi，zi)，其中i=1，2，…，n，终点坐标为pg(xg，yg，zg)。为简化问题，规划过程中，步长S在水平面内的投影为定值。这样每一步搜索只需要寻找最优的前进角度ψ、θ即可。每步规划中，首先建立UUV路径规划代价函数，然后利用粒子群算法在搜索空间寻找具有最优代价函数路径点，从而得到下一个路径点。

2.1 躲避障碍代价函数

海洋环境中存在海底山脉、礁岩、暗桩等固定障碍。如图3所示，为实现对固定障碍的有效规避，需要建立UUV躲避障碍代价函数。

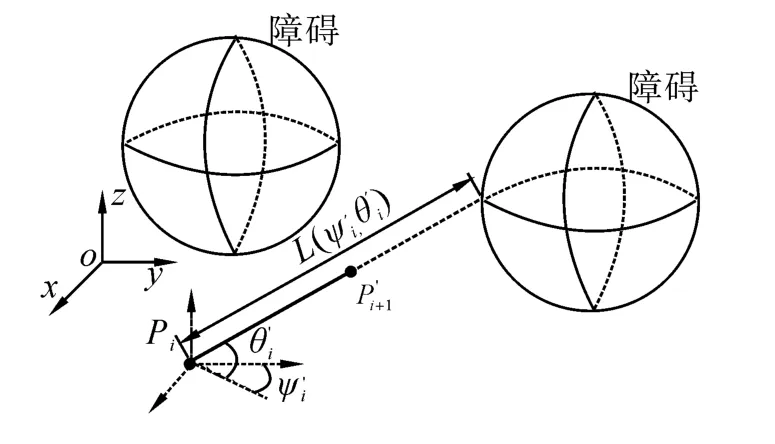
图3 UUV路径规划示意图Fig.3 UUV path planning schematic

UUV在前行方向上距障碍物越远，代价函数越大，反之代价函数越小。如图3所示，当前点Pi在规划下一点候选点方向上到障碍物的直线距离为，步长为S，从而躲避障碍代价函数为

式中，fmax是一较大数值，如果候选点遭遇障碍，则代价函数等于较大数值，UUV前行过程中始终寻找f1小的点，从而实现对固定障碍物的规避。

利用之前所述的UUV最小离地高度，可以计算出确定艏向角ψ时，下一路径点处UUV最小离地高度，进而计算出该路径点的纵倾角θ，即有

从而躲避障碍代价函数为自变量为ψ的一维代价函数，式(4)也可化为

2.2 趋近目标代价函数

为实现UUV朝向目标运动，需要建立趋近目标代价函数。如图4所示。

图4 趋近目标示意图Fig.4 Schematic of reaching the target

当前点Pi与终点Pg连线的角度为(ψi，θi)，候选点的角度为，UUV朝向目标点运动，即有(ψi，θi)与越相近时趋近目标代价函数越大，(ψi，θi)与差值越大，趋近目标代价函数越小。从而有趋近目标代价函数:

2.3 UUV路径规划总代价函数

UUV路径规划总代价函数为躲避障碍代价函数与趋近目标代价函数的叠加。从而有

式中:ki为权重系数(ki＞0)。UUV在当前点规划路径时，利用改进的粒子群算法寻找代价函数小的点，将找到的点作为下一时刻UUV航行路径。

3 改进粒子群优化算法

粒子群优化算法概念和参数调节都比较简单，易于实现，具有较强的寻优能力。一经提出便受到广泛关注，许多专家学者对其进行了深入的研究和分析，提出了很多改进策略，以提高算法的性能。典型的改进算法有 BPSO、LWPSO、EPSO、TVAC 等［9-12］。

1)基本粒子群优化算法(basic particle swarm optimization，BPSO):

式中:vid(k)表示第k次迭代中的第i个粒子第d维的进化速度，ci(i=1，2)表示学习因子，ri(i=1，2)是［0，1］的随机数，pid(k)表示第k次迭代后第i粒子历史最优位置第d维坐标;pgd(k)表示第k次迭代后种群最优粒子第d维坐标。

2)线性时变惯性权重粒子群优化算法(linearly varying inertia weight particle swarm optimization，LWPSO):

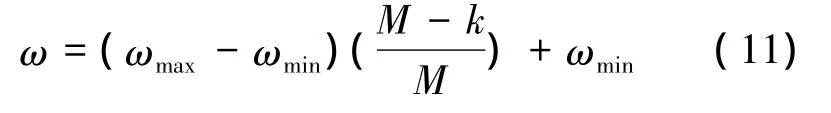
即在BPSO基础上，采用式(11)的惯性权重。搜索初期惯性权重比较大，随着搜索的进行，惯性权重线性下降，搜索后期惯性权重较小。其中ωmax表示最大惯性权重，ωmin表示最小惯性权重，M表示最大迭代次数。

3)指数时变惯性权重粒子群优化算法(exponential inertia weight particle swarm optimization，EPSO):

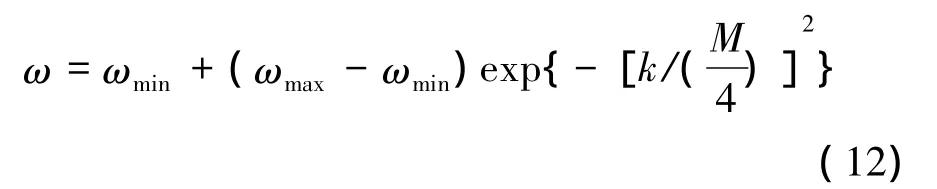
在BPSO的基础上采用式(12)随着迭代的进行惯性权重成指数下降。其中M为最大迭代次数，k是当前迭代次数。

4)具有时变加速因子的自组织粒子群优化算法(time-varying acceleration co-efficient，TVAC):

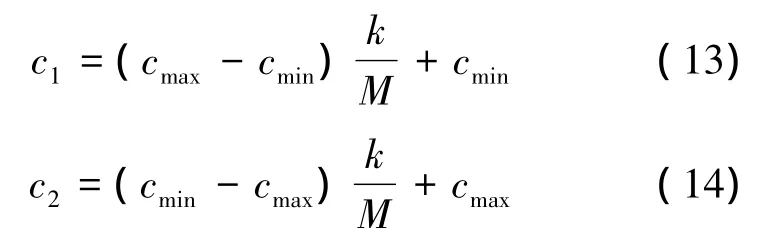
即在BPSO基础上搜索初期c1＞c2提高搜索初期的全局搜索能力，搜索后期c1＜c2有利于粒子收敛于全局最优解。其中cmax表示最大学习因子，cmin表示最小学习因子。

影响粒子群搜索性能的因素主要有自身惯性速度，自身历史最优位置，以及群体历史最优位置3种因素。为有效利用这些因素，本文提出一种改进的粒子群优化算法(novel particle swarm optimization，NPSO)，将群体中粒子编号，每次迭代，按粒子序号顺序计算子粒子代价函数。粒子初始进化时，应具有较大的惯性权重，粒子更侧重于自身经验的搜索，以增强全局搜索能力。所有粒子均取参数组合1:较大的惯性权重ω=ωmax，较大的自身经验学习因子c1=cmax，较小的群体经验学习因子c2=cmin。如果粒子代价函数较上次迭代的代价函数更优，则继续采用参数组合1。若粒子代价函数并不比上次迭代的历史最优代价函数更优，则说明粒子接近较优点，此时，应采用较小的惯性权重，加强局部搜索，而且粒子进化侧重于群体经验，粒子向群体最优点运动。故从下个粒子进化开始采用参数组合2:较小的惯性权重ω=ωmin，较小的自身经验学习因子c1=cmin，较大的群体经验学习因子c2=cmax。如果粒子代价函数较上次迭代的代价函数更优，则采用参数组合1。如果粒子最优代价函数始终不变，则粒子可能进入局部最优点，应再次加大自身经验的比重。因此参数组合2改为:较小的惯性权重ω=ωmin，学习因子随着迭代次数的增加而变化，有

其中:

式中，k表示当前迭代次数，k0表示采用参数组合2时的迭代次数，N为常系数。

4 算法性能分析

为衡量算法的性能，采用不同的测试函数对算法进行测试，并将 NPSO与 BPSO、LWPSO、EPSO、TVAC 性能进行比较［9-12］。

采用的测试函数为

1)sphere函数:

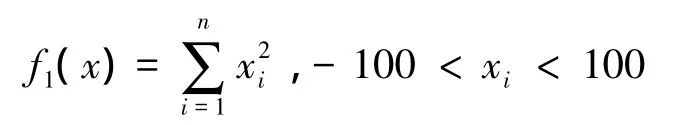
2)Rotated hyper-ellipsoid函数:

3)Rosenbrock函数:

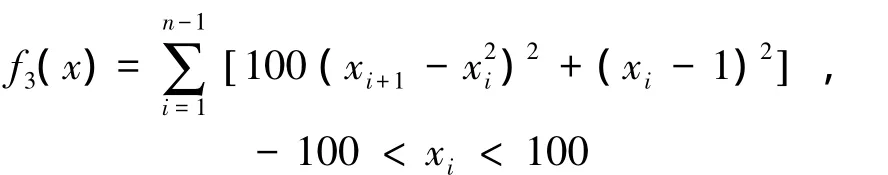
4)Rastrigin函数:

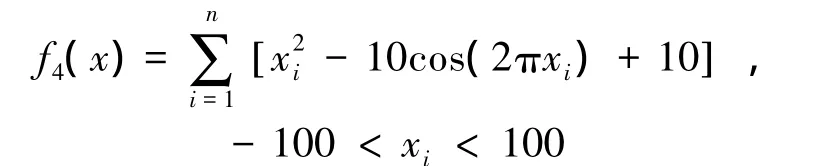
5)Griewank函数:

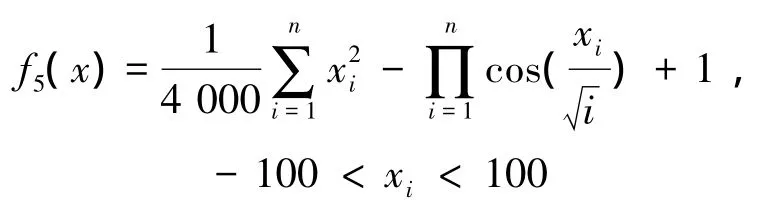
仿真时，对于 NPSO、BPSO、LWPSO、EPSO、TVAC取种群粒子个数为n=30。学习因子取c1=c2=2．0，自变量维数D=10，惯性因子ω设为 0．7，ωmax设为 0．9，ωmin设为0．4，cmax=2．5，cmin=0．5，N=10，最大迭代次数为 1 000。搜索空间xi∈[-100，100]，速度变量vi∈ [-100，100]，搜索过程中，如果粒子位置超出边界，则此时边界坐标设为粒子位置坐标，并将速度设为零。如果速度超出边界，则将速度边界值设为速度值。为了获得更加准确的仿真结果，对每个函数的优化都重复100次，每次都迭代1 000次，对得到的100个结果求取平均数和标准差，仿真结果如表1所示。

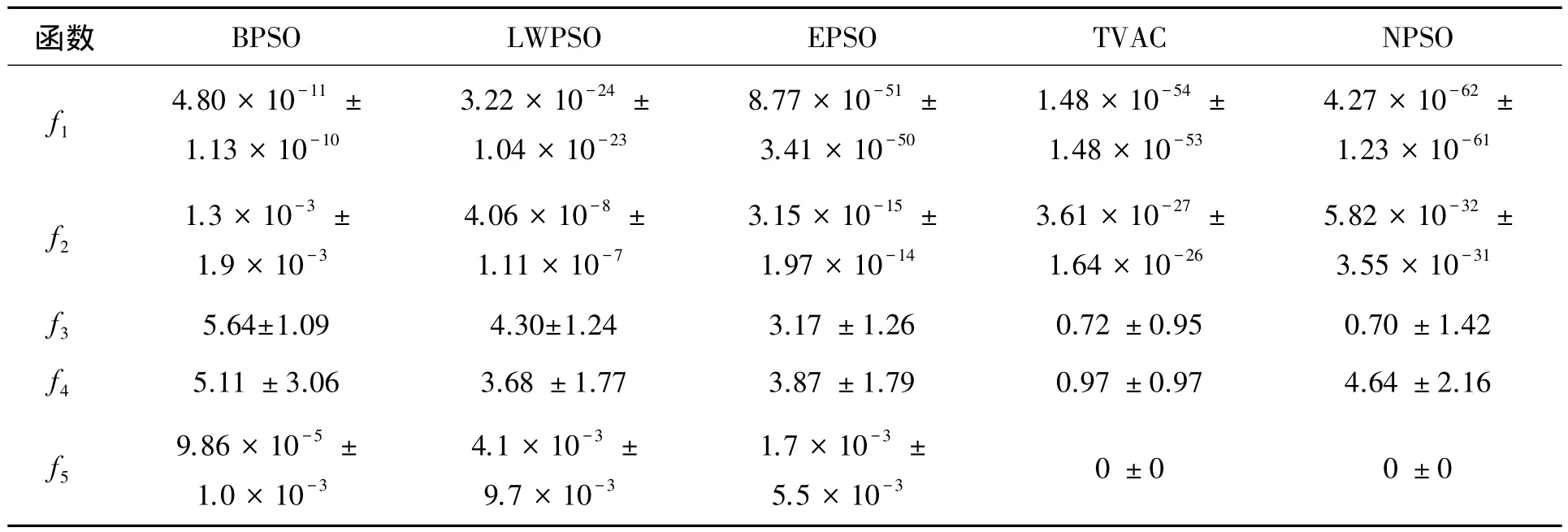
表1 BPSO、LWPSO、EPSO、TVAC和NPSO对比结果Table 1 Comparison results of BPSO，LWPSO，EPSO，TVAC and NPSO

由表1可以看出，对于单模态函数，搜索精度和稳定性由低到高依次为 BPSO、LWPSO、EPSO、TVAC、NPSO，唯独对于高度多模态 Rastrigin函数NPSO搜索效果并不理想。Rosenbrock函数f3和Griewank函数f5进化过程中的平均适应度变化如图5所示。由图5中可以看出，搜索速度由快到慢依次为 TVAC、NPSO、EPSO、LWPSO、BPSO。其中NPSO与TVAC的搜索速度相当。

为验证算法在不同维数下的性能，对测试函数，维数从10维增加到100维，分别计算了4种算法作用下结果的均值和标准差。表2给出了Rosenbrock函数由10维增加到100维的部分实验数据。由表2可知，随着测试函数维数的增加各搜索算法的搜索精度和稳定性均存在不同程度的下降，而总体来看TVAC与NPSO算法的搜索精度和稳定性要优于其他算法。

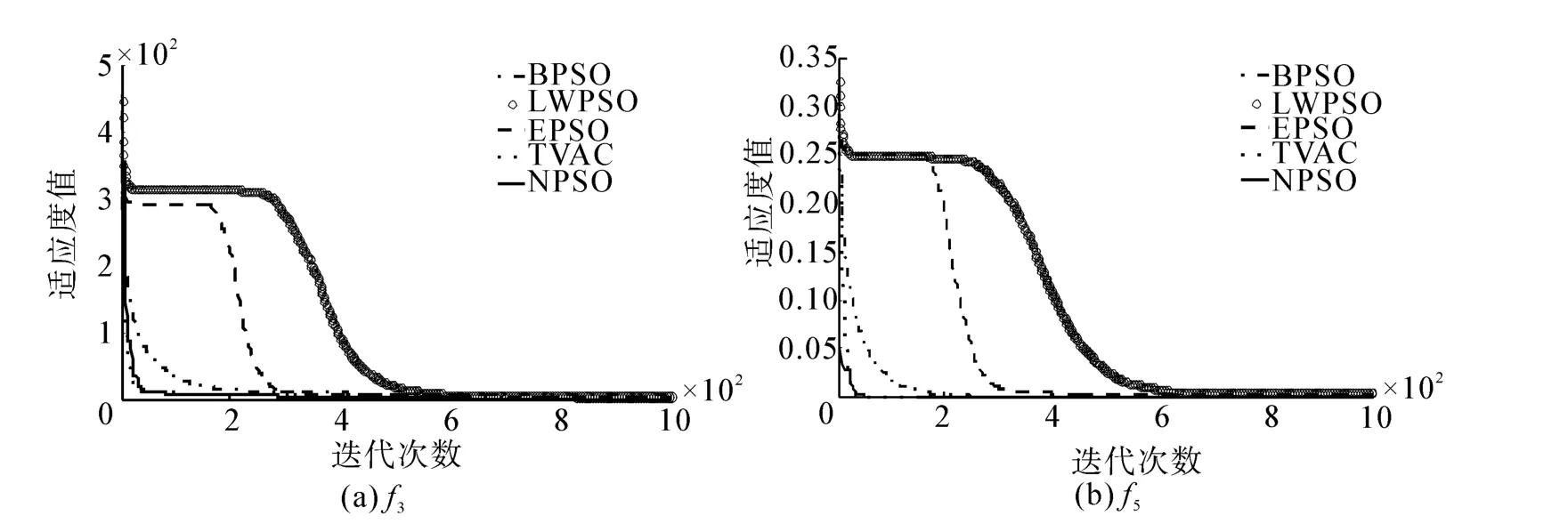
图5 平均适应度变化曲线图Fig.5 Curves of average fitness

表2 Rosenbrock函数不同维数下BPSO和GHEPSO对比结果Table 2 Comparison results of BPSO and GHEPSO on Rosenbrock function under the different dimensions

5 UUV路径规划仿真

建立 UUV航行过程中近海底代价函数，将NPSO用于寻找代价函数小的点，将找到的点作为下一时刻UUV航行路径。对所提方法进行仿真验证。

图6 UUV路径规划仿真图Fig.6 UUV path planning simulation

选取海底三维地形图的一部分{［0，14］，［0，17］，［0，-0.3］}km 作为规划空间。取起始点为(2，2，-0.17)km，目标点为(11，15，-0.125)km。纵倾角约束为，艏向角约束为ψmax=60°，其中Δψ为相邻2个路径段之间艏向角的变化，仿真结果如图6所示。由图6可以看出，UUV可以很好地规避障碍威胁，在安全航行高度近海底航行，得到了有效地近海底航行路径。

6 结束语

为实现UUV近海底航行，综合考虑地形约束以及UUV自身性能约束，提出了UUV近海底航行安全深度计算方法，同时，将基本粒子群算法进行了改进，然后利用几个典型的测试函数对NPSO的性能进行了分析。结果表明，对于单模态函数NPSO在搜索精度、稳定性和搜索速度上均优于BPSO、LWPSO、EPSO、TVAC，对于多模态函数 NPSO性能与BPSO相当。在UUV近海底空间路径规划过程中，结合UUV近海底安全航行高度建立UUV近海底路径规划代价函数，利用粒子群算法对代价函数寻优，找到较优的路径点。仿真结果显示，UUV可以在近海底安全航行高度上实现对地形威胁和障碍威胁的规避，并朝向目标点航行，最终得到安全有效的近海底航行路径。

［1］LIU Liqiang，DAI Yuntao.3D space path planning of complex environmental underwater vehicle［C］//International Joint Conference on Computational Sciences and Optimization.Sanya，China，2009:204-209.

［2］郝燕玲，张京娟.基于遗传算法的AUV三维海底路径规划［J］.中国工程科学，2003，5(11):56-60.HAO Yanling，ZHANG Jingjuan.AUV path planning in 3D seabed environment using genetic algorithm［J］.Engineering Science，2003，5(11):56-60.

［3］NATHAN E B.Three-dimensional route planner usingA*algorithm application to autonomous underwater vehicles［R］.Baton Rouge:Louisiana State University，2008.

［4］武善杰，郑征，蔡开元.基于行为协同和虚拟目标相结合的无人机实时航路规划［J］.控制理论与应用，2011，28(1):131-136.WU Shanjie，ZHENG Zheng，CAI Kaiyuan.Real-time path planning for unmanned aerial vehicles using behavior coordination and virtual goal［J］.Control Theory and Applications，2011，28(1):131-136.

［5］朱毅，张涛，宋靖雁.非完整移动机器人的人工势场法路径规划［J］.控制理论与应用，2010，24(2):154-161.ZHU Yi，ZHANG Tao，SONG Jingyan.Path planning for nonholonomic mobile robots using artificial potentical field method［J］.Control Theory and Application，2010，24(2):154-161.

［6］MONDAL D，CHAKRABARTI A，SENGUPTA A.Optimal placement and parameter setting of SVC and TCSC using PSO to mitigate small signal stability problem［J］.International Journal of Electrical Power and Energy Systems，2012，42(1):334-340.

［7］ISHAQUE K，SALAM Z，AMJAD M，et al.An improved particle swarm optimization(PSO)-based MPPT for PV with reduced steady-state oscillation［J］.IEEE Transactions on Power Electronics，2012，27(8):3627-3638.

［8］MOHAMMADI-IVATLOO B，RABIEE A，SOROUDI A，et al.Iteration PSO with time varying acceleration coefficients for solving non-convex economic dispatch problems［J］.International Journal of Electrical Power ＆ Energy Systems，2012，42(1):508-516.

［9］张顶学，关治洪，刘新芝.一种动态改变惯性权重的自适应粒子群算法［J］.控制与决策，2008，23(11):1253-1257.ZHANG Dingxue，GUAN Zhihong，LIU Xinzhi.Adaptive particle swarm optimization algorithm with dynamically changing inertia weight［J］.Control and Decision，2008，23(11):1253-1257.

［10］RATNAWEERA A，HALGAMUGE S K，WATSON H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients［J］.IEEE Transactions on Evolutionary Computation，2004，8(3):240-255.

［11］SHI Y，EBERHART R.A modified particle swarm optimizer［C］//Evolutionary Computation Proceedings.Anchorage，USA，1998:69-73.

［12］CHEN G，HUANG X，JIA J，et al.Natural exponential inertia weight strategy in particle swarm optimization［C］//Intelligent Control and Automation.Dalian，China，2006:3672-3675.