基于预测模型的模糊参数自寻优S面控制器

何斌，万磊，姜大鹏，张国成

(1.哈尔滨工程大学 船舶工程学院，黑龙江哈尔滨150001;2.哈尔滨工程大学 水下机器人技术重点实验室，黑龙江 哈尔滨150001)

潜水器是一个多变量、强耦合且高度非线性的动力学系统，加之环境的不确定性、时变性以及任务的复杂性，使得在潜水器运动控制研究中依赖于精确数学模型的传统控制方法显得有些不足，目前该领域的专家主要将精力集中在现代控制及智能控制方法上［1］。S面控制算法是刘学敏等提出的一种结合了PID控制和模糊控制的混合控制算法，在多个潜水器的海试中取得了良好的控制效果［2-4］。

潜水器自身载荷以及外界环境的时变性要求S面控制器参数能够实时调整，人工调参不仅占用大量的人工时间，而且对环境变化不够灵敏。研究人员将粒子群优化算法［5］、模糊控制［6］、专家控制［7］、预测控制［8］等引入到S面控制器参数调整中，做了大量研究工作。基于模糊规则的参数调整方法具有参数少、易实现的优点;基于预测模型的参数调整方法能够解决潜水器状态信息滞后的缺点，但其反馈优化环节普遍具有在线计算量大的缺点［9］。本文结合预测控制的思想，为基于模糊规则的参数自寻优S面控制方法提供超前的状态信息，同时也避开了基于预测模型的参数自寻优方法中在线计算量大的不足。

1 潜水器预测模型的建立

1.1 基于Elman神经网络的模型辨识

1.1.1 系统描述

针对潜水器动力学系统的高度非线性、强耦合性，本文采用NARMA模型来描述潜水器的动力学特征。NARMA模型是一种用关于带时滞输入、输出的非线性函数来表示系统动态特征的模型［10］。潜水器的NARMA预测模型可以表示为

式中:x(t)= ［y(t-1)，…，y(t-n)，u(t-d)，…，u(t-d-m)］T;y=［ξ，η，ζ，φ，θ，ψ，u，v，w，p，q，r］T为潜水器的状态信息;u=［Xτ］T为控制器解算得到的6自由度所需的推力(矩);FENN(˙)为非线性函数，采用Elman神经网络辨识得到。

1.1.2 Elman 神经网络及应用注意

Elman神经网络属于局部回归网络，其内部反馈机制体现其能够映射动态过程的能力［11］。本文采用Elman神经网络对潜水器的NARMA模型进行辨识以提高预测模型适应时变环境的能力。Elman神经网络结构如图1所示，相对于常规3层前馈网络，其增加的状态层用来储存隐含层上一时刻的输出值，状态层单元作为一步延时算子起到记忆过去状态的作用。Elman神经网络的状态空间表达式［11］为

式中:y(t)为系统t时刻的输出，u(t)为系统t时刻的输入，xc(t)为状态层t时刻的输入，x(t)为隐含层t时刻的输入，w(1)为状态层至隐含层的权值矩阵，w(2)为输入层至隐含层的权值矩阵，w(3)为隐含层至输出层的权值矩阵，θ(1)、θ(2)分别为隐含层和输出层神经元的阈值矩阵，f(˙)与g(˙)为隐藏层和输出层神经元的激活函数。

Elman神经网络的学习算法可参考文献［11］。下面给出采用BP算法得到的权值矩阵w(1)、w(2)和w(3)的修正量:

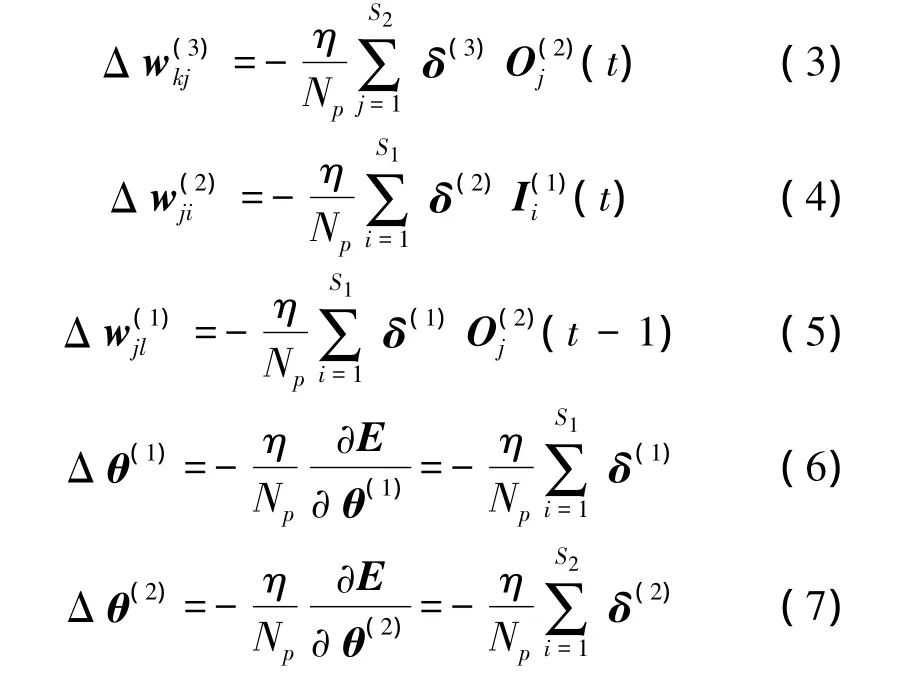
式中:i、j、k、l分别为输入层、隐藏层、输出层和状态层的神经元序列，η为学习率，NP为学习样本容量，S1、S2、S3为输入层、隐含层及输出层的神经元节点数分别为输入层、隐藏层、输出层及状态层的输入分别为输入层、隐藏层、输出层及状态层的输出为状态层到隐含层的反馈误差信号，为输入层到隐含层的反馈误差信号为隐含层到输出层的反馈误差信号。

图1 Elman神经网络结构Fig.1 Structure of Elman neural network

应用Elman神经网络时以下2点值得注意:

1)权值矩阵初值的设置对网络学习结果的最佳程度会有影响，因此将权值矩阵的初值w(1)(0)、w(2)(0)和w(3)(0)设置为在［0，1］区间均匀分布的随机数。

2)与BP网络类似，Elman网络的学习率太大会导致收敛振荡，太小会导致收敛过慢，改进办法是在权值修正表达式里加入惯性调整项，将权值与阈值的调整量统一用ΔM表示，改进后的“惯性”调整算法为

式中:β为惯性系数，ΔM(t)表示t时刻的权值或阈值的调整量，ηN(t+1)为t+1时刻由式(3)～(7)得到的权值或阈值修正量。

β的值越大，则每一次的系数调整量受前一次的调整量的影响越大，若t+1时刻权值调整的符号与t时刻一致，则表示调整方向的正确性，将2次调整量相加以加快调整速度;反之则相减，以减缓调整速度。实验证明，η和β选取的都较大或较小时，可以达到相似的收敛结果，只是前者的学习速度要相对快得多。

1.2 基于在线辨识的改进

如果只采用离线辨识好的模型进行预测，当环境(内在及外界)变化时预测结果将不再可信，辨识网络需根据系统实时的输入输出信息进行在线学习，达到误差限后更新权值，以建立新的预测模型。

网络训练耗时过长是在线辨识过程中最重要的问题之一，随着时间的推移学习样本的容量会越来越大，网络训练所需的时间也会越来越长，甚至在一个控制节拍内不能完成学习。为了解决以上问题，本文从样本容量和预测模型结构进行了考虑。

1.2.1 滚动样本法的应用

图2 滚动样本法Fig.2 Schematic diagram of rolling samples method

N值的设定要以实际系统的计算能力为依据，在处理器允许的情况下较大的N值能够加速网络的收敛。为了对N值进行初步估计，本文首先在水面监控工作机上利用MATLAB进行了离线辨识实验。

实验所需样本选自某潜水器定艏向控制水池实验数据，待辨识NARMA模型的输入输出阶数分别为m=1、n=3，系统时滞d=1，即{y(t-1)，y(t-2)，y(t-3)，u(t)，u(t-1);y(t)}为一组样本。Elman网络有一层隐含层，输入输出层节点数分别为5和1，隐含层节点数为15，隐含层的传输函数取tansigS函数，输出层的传输函数取purelin线性函数，训练步长设为200。离线辨识结果如图3所示，校验样本容量为150。当训练样本容量为300时网络达到误差限的迭代步数在100步左右(多次实验)，时间消耗在0.1 s之内。因此可选择300作为N的初始值，实际实验时须进行逐步修正。

图3 艏向离线辨识结果Fig.3 Results of heading off-line identification

1.2.2 预测模型结构的改进

网络训练一般采用设置学习误差限和限定学习步长相结合的方式来结束一个节拍内的学习。而通过设置学习步长强行停止训练会导致建立的预测模型不准确;某些情况下即使采用滚动样本法来减少网络学习时间，在线辨识网络仍然不能在一个控制节拍内收敛到误差限，从而不得不在限制步数到来时停止学习。鉴于此，本文采用并行神经网络的思想［12］，将在线辨识网络并列加入到预测网络中，以改善预测模型的在线辨识性能，其结构如图4所示。图中，u(t)为控制器输出的控制指令;yu(t+d)为潜水器的实际输出;ym(t+d|t)、ym＇(t+d|t)为模型预测输出;em＇(t+d|t)为在线辨识网络的预测误差;z-1为单位延迟算子。预测网络使用上一次学习得到的网络权值进行预测输出，在线辨识网络则以学习误差限为停止学习的主要依据，进行多个节拍的学习，直到满足误差限要求，即em＇(t+d|t)＜emax，然后更新预测网络的权值矩阵，以此改善模型的在时变环境下的预测能力。

图4 改进的辨识模型结构Fig.4 Improved identification structure

2 基于模糊规则的参数自寻优方法

S面控制算法表达式如下:

式中，被控量的偏差e与偏差变化率e·为控制器的输入，u为控制器的输出，k1、k2分别表示某个自由度被控量的偏差和偏差变化率对应的参数，Δu表示通过自适应调整得到的某段时间上的固定干扰力，风浪流、重力和浮力的变化以及其他一些未知因素可视为一段时间里的固定干扰力。以上变量均经过归一化处理。

对于潜水器各自由度之间的耦合，实际处理时为除横摇之外的5个自由度分别设计1个S面控制器，实现对潜水器运动的有效控制。从S面控制算法表达式可以看出S面控制在形式上和PD控制很相似，S面控制包含2个控制参数k1和k2，与PD控制的2个参数相对应，并且含义相同，只不过后者是线性的，前者是非线性的。当然，采用非线性函数来拟合非线性系统比采用线性函数更好一些［14］。通过改变k1和k2的大小可以调整偏差和偏差变化率在控制输出中所占的比重，从而调节控制的超调和收敛速度以满足作业的要求。

深栽造林用到的乌柳枝干春季截取母树上生长健壮的1～3年生萌生粗壮枝，插干大头直径在2～4cm。选择无机械损伤，无抽条干缩，无畸形，无弯曲和无病虫害的枝条。剪除枝条全部的抽条，剪取枝条中部作插干，插干长约110～120cm。

经过大量的潜水器仿真和外场实验，研究人员［2，4，6］已经针对各自由度 S 面控制器的参数实时调整总结出一些经验和知识。应用模糊推理可以方便地将研究人员的经验与思考归纳为系统化的规则并实现对参数的调节。S面控制器基于模糊规则的参数自寻优方法可参见文献［13］，下面给出本文的处理过程。

1)基本论域及尺度变换:模糊推理的输入量为各自由度的位姿偏差及偏差变化率，输出量为各自由度的S面控制器参数。变量基本论域需根据具体实验环境下输入量、输出量的变动范围进行初步估计，在具体调试和实验过程中须进行不断修正;模糊推理尺度变换所要求的论域选择［-1，1］。

2)模糊空间分割及隶属度函数的选择:将模糊推理输入空间分为7档，将输出空间分为5档，隶属度函数选用对称、均匀分布、全交叠的三角形隶属度函数。

3)模糊化与清晰化:模糊推理的输入量采用单点模糊集合表示

式中:A为输入空间对应的模糊集合，μA(e)为模糊集合A的隶属度函数。对k1、k2的清晰化处理采用加权平均法:

式中:μC'(ki)为ki对应模糊集合C'的隶属度函数，为得到的清晰变量。

4)模糊规则:由于输出量k1、k2相对独立，因此系统为2个输入(e和)，单输出(k1或者k2)系统，以k1为例，参数调整规则见表1。

表1 参数k1模糊调整规则Table 1 Fuzzy adjusting rules of k1

5)模糊推理:本文采用广义肯定式推理，计算公式如下

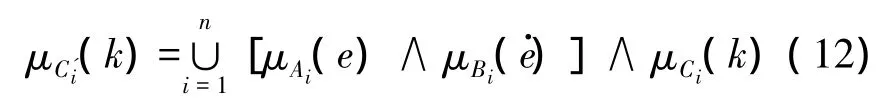
式中:Ai、Bi、Ci分别为输入空间、输出空间对应的模糊集合;μAi(·)、μBi(·)、μCi(·)分别为模糊集合Ai、Bi、Ci的隶属度函数;μAi(e)∧μBi()可以理解为第i条规则的加权因子。

3 基于预测模型的模糊参数自寻优S面控制器

下面将前文建立的预测模型应用到基于模糊规则的参数自寻优S面控制器中。基于预测模型的模糊S面控制器结构如图5所示。

图5 基于预测模型的模糊S面控制器结构Fig.5 Fuzzy S surface controller based on prediction model

基于预测模型的模糊S面控制器包括4个模块:基本S面控制器模块、预测模型模块、反馈校正模块和基于模糊规则的参数调整模块。基本S面控制器模块可参考文献［14］。

为了避免由于模型失配引起控制失效，需要时刻检测系统实际输出与预测模型输出的误差，对预测输出进行实时校正，使参数在线自寻优建立在误差反馈校正的基础上，以提高了系统的稳定性。反馈校正按下式计算:

式中:y(t+d)为t时刻系统的实际输出，ym(t+d|t)为t时刻预测模型的预测输出。

基于预测模型的模糊参数自寻优方法可用下式表示:

式中:k1(t)、k2(t)为模糊推理得到的t时刻各自由度的控制器优化参数;FISm为基于Mamdani蕴含运算的模糊推理系统;FENN为非线性函数，由Elman神经网络辨识;e(t+d|t)、(t+d|t)为系统经过模型预测、反馈校正后，与期望状态比较得到的t时刻各自由度的偏差和偏差变化率;yt(t)为t时刻实验载体的期望状态;yp(t+d|t)为t时刻由预测模型经反馈校正后各自由度的预测输出;ym(t+d|t)为t时刻由预测模型得到的各自由度的预测输出;y(t+d-i|t)为t-i时刻的系统输出，其取值按下式计算:

文献［15］从位置控制和速度控制2个方面出发，分析了S面控制方法在潜水器运动控制中的稳定性问题。该文中将纵向S面控制表达式进行线性化处理，得到纵向PD控制器。通过选取能量函数作为李雅普洛夫函数，证明了纵向PD控制器的稳定性。然后根据T-无源理论证明了非线性的S面控制方法是李雅普洛夫稳定的，并得到了S面控制器的参数设计准则，即k1＞0，k2＞0。

本文的工作是在预测模型基础上通过模糊推理实现S面控制器参数的自寻优。离线辨识实验检验了Elman神经网络的在一定训练样本数量下的收敛性，并由此得到了在收敛时间和系统性能之间平衡的滚动样本数量;并行神经网络的辨识结构保证了预测值的置信度(在线学习网络收敛后再将网络权值传递给预测网络)，因此，只要保证模糊推理规则库中S面控制器参数均大于零，就能保证控制系统的稳定。

4 仿真实验及分析

为了验证改进后的参数自寻优S面控制器的性能，将普通S面控制器、基于模糊规则的参数自寻优S面控制器和基于预测模型的模糊参数自寻优S面控制器与潜水器运动仿真平台联机进行仿真实验，潜水器运动仿真平台的建立可参考文献［16］，下面将纵向运动控制和艏向运动控制的仿真实验结果进行比较分析。

图6为纵向运动控制实验结果曲线。初始纵向位置为0 m，目标纵向位置为3 m，S面控制器的初始参数设置为k1=2，k2=5。

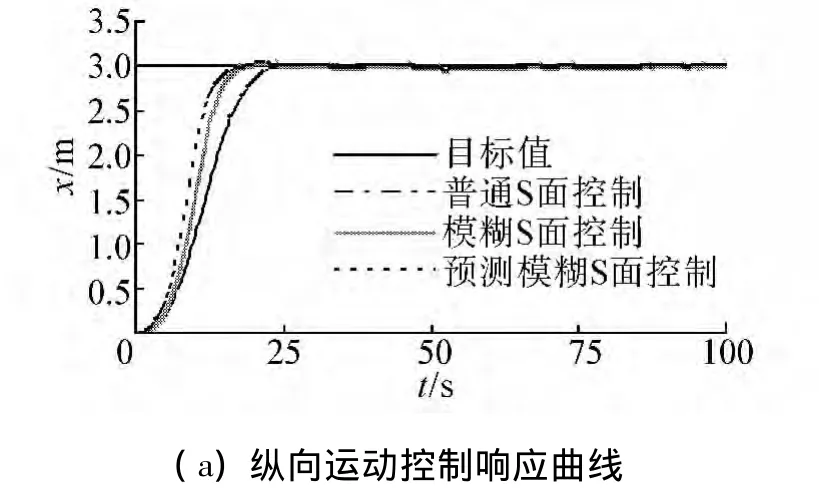
图7为艏向运动控制实验结果曲线。初始艏向角为0°，目标艏向角为30°，S面控制器的初始参数设置为k1=1，k2=3。

图7 艏向运动控制实验结果Fig.7 Results of heading control

由图6(a)、7(a)，纵向、艏向运动在基于预测模型的模糊参数自寻优S面控制器作用下达到目标值的响应时间为18 s和17 s，相应在模糊S面控制器作用下的响应时间为21 s和22 s，在普通S面控制器作用下的响应时间为25 s和33 s。可见基于预测模型的模糊参数自寻优S面控制器在控制响应速度方面优于其他2种控制器;

由图6(b)、7(b)，应用基于预测模型的模糊参数自寻优S面控制器时，系统的推力、力矩输出较其他2种控制器更为灵敏，推力输出的负值部分体现其对控制超调的提前制动能力，这是快速趋近目标的意志体现。图6(b)中显示推力输出出现了震荡，原因是运动仿真程序中对速度传感器的模拟加入了高斯噪声，以模拟真实的水声环境，而纵向位置控制输出需要采集速度传感器数据作为偏差变化率，由此计算得到的推力就出现了震荡的现象;而图7(b)中转艏力矩没有出现类似的震荡现象，因为姿态传感器的输出较依赖于水声环境的速度传感器要更加平稳。

图6(c)、7(c)为基于预测模型的模糊参数自寻优S面控制器和模糊参数自寻优S面控制器的参数自寻优过程，在偏差缩小的控制响应过程中，k1先增大后减小，k2先减小后增大，体现了模糊规则的思想。

在超调量和稳态误差方面3种控制器没有明显差异，这与仿真平台的逼真度存在一定的关系。

5 结论

本文针对S面控制器的参数调整问题，结合模糊控制与预测控制的思想，探讨了基于预测模型的模糊参数自寻优方法，由仿真实验结果可得到以下结论:

1)该方法所选的NARMA模型能够反映潜水器的动态特征，将其作为潜水器的预测模型是可行的;

2)采用并行Elman神经网络对本文建立的NARMA模型进行模型辨识能够满足仿真实验要求;

3)将建立的预测模型加入基于模糊规则的参数自寻优S面控制器中能够提升控制器的控制响应速度，可为潜水器执行时限任务时争取更多的有效时间，具有重要的实际意义。

不足之处在于改进的S面控制器的稳定性没有在复杂海洋环境下进行测试，这是以后值得研究的问题。

［1］张铁栋.潜水器设计原理［M］.哈尔滨:哈尔滨工程大学出版社，2011:162-182.

［2］LI Ye，PANG Yongjie，WAN Lei，et al.A fuzzy motion control of AUV based on apery intelligence［C］//Proceedings of 2009 Chinese Control and Decision Conference.Guilin，China，2009:1316-1321.

［3］WANG Jianguo，WU Gongxing，WAN Lei，et al.Motion control of underwater robot based on an improved controller［C］//Proceedings of 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems.Shanghai，China，2009:694-699.

［4］SUN Yushan，WAN Lei，LI Yueming，et al.S plane control based on parameters optimization with simulated annealing for underwater vehicle［C］//Proceedings of 2011 International Conference on Electronic and Mechanical Engineering and Information Technology.Harbin，China，2011:552-556.

［5］郭冰洁，徐玉如，李岳明.水下机器人S面控制器的改进粒子群优化［J］.哈尔滨工程大学学报，2008，29(12):1277-1282.GUO Bingjie，XU Yuru，LI Yueming.S surface controller for underwater vehicles using particle swarm optimization［J］.Journal of Harbin Engineering University，2008，29(12):1277-1282.

［6］吕翀.自主式水下机器人智能控制［D］.哈尔滨:哈尔滨工程大学，2008:24-35.LYU Chong.Intelligent motion control of autonomous underwater vehicle［D］.Harbin:Harbin Engineering University，2008:24-35.

［7］ZHANG Lei，PANG Yongjie，SU Yumin，et al.Expert S-surface control for autonomous underwater vehicles［J］.Journal of Marine Science and Application，2008，7(4):236-242.

［8］WANG Fang，WAN Lei，SU Yumin，et al.AUV modeling and motion control strategy design［J］.Journal of Marine Science and Application，2010，9(4):379-385.

［9］高萍.基于神经网络的水下机器人广义预测控制技术研究［D］.哈尔滨:哈尔滨工程大学，2007:22-28.GAO Ping.Study on generalized predictive control of autonomous underwater vehicles based on neural network［D］.Harbin:Harbin Engineering University，2007:22-28.

［10］罗秋滨.一类非线性系统预测控制中的建模问题［D］.哈尔滨:哈尔滨工业大学，2008:19-41.LUO Qiubin.Modeling problems in nonlinear predictive control［D］.Harbin:Harbin Institute of Technology，2008:19-41.

［11］郭健.基于智能算法的非线性模型研究及预测控制［D］.武汉:华中科技大学，2008:69-78.GUO Jian.Study on nonlinear model and predictive control based on intelligent algorithm［D］.Wuhan:Huazhong U-niversity of Science and Technology，2008:69-78.

［12］甘永.水下机器人运动控制系统体系结构的研究［D］.哈尔滨:哈尔滨工程大学，2007:75-86.GAN Yong.Research on motion control system architecture of underwater vehicle［D］.Harbin:Harbin Engineering University，2007:75-86.

［13］赵云峰，宋立维，吴志勇.基于模糊算法的Sigmoid函数的AUV控制［J］.微计算机信息，2009，25(8):267-269.ZHAO Yunfeng，SONG Liwei，WU Zhiyong.AUV control using sigmoid function with fuzzy algorithm［J］.Microcomputer Information，2009，25(8):267-269.

［14］刘学敏，徐玉如.水下机器人运动的S面控制方法［J］.海洋工程，2001，19(3):81-84.LIU Xuemin，XU Yuru.S control of automatic underwater vehicles［J］.The Ocean Engineering，2001，19(3):81-84.

［15］李岳明.多功能自主式水下机器人运动控制研究［D］.哈尔滨:哈尔滨工程大学，2013:25-31.LI Yueming.Research of multifunction autonomous underwater vechile motion control［D］.Harbin:Harbin Engineering University，2013:25-31.

［16］常文君，刘建成，于华男，等.水下机器人运动控制与仿真的数学模型［J］.船舶工程，2002，24(3):58-60.CHANG Wenjun，LIU Jiancheng，YU Huanan，et al.A mathematical model for motion control and simulation of underwater vehicle［J］.Ship Engineering，2002，24(3):58-60.