潜礁上孤立波传播的数值模拟

房克照，刘忠波，唐军，邹志利，尹继伟

(1.大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024;2.国家海洋局海洋环境检测中心，辽宁大连116023;3.大连海事大学交通运输管理学院，辽宁大连116026;4.长沙理工大学水沙科学与水灾害防治湖南省重点实验室，湖南长沙410076)

数值模拟研究海啸波的传播以及爬高等问题具有十分重要的意义。当近岸潜礁存在时，由于其前坡较为陡峭且潜礁内平台水深较小，海啸波的传播形态和能量组成将产生显著变化，较一般开阔海岸上更为复杂［1］。数值模拟时，不仅要求模型能够描述非线性海啸波的传播过程，还要具备处理波浪破碎和海岸动边界问题的能力。此外，海啸波在近岸潜礁上传播容易形成水跃，具有极其陡峭的波面形态，要求模型具有较强的间断捕捉能力［1-2］。

通常采用非线性浅水方程结合孤立波数值研究海啸波的传播、破碎和爬高过程［3-4］。非线性浅水方程是典型的双曲型模型，已有大量的高精度数值求解格式［5］。不但拥有高分辨率特征，同时能较方便地处理波浪破碎和海岸动边界问题，基于非线性浅水方程和利用高精度数值方法建立的海啸波传播数学模型取得了较大的成功［3-4］。但该方程存在重大缺陷:缺乏色散性，使得其仅能应用于模拟近岸海啸波传播，大大限制了其应用范围。而近几十年来发展得的Boussinesq类水波方程［6］，虽然精度各异，但其既包含色散性又包含非线性，具备模拟海啸波传播的潜质。但是这类模型对于波浪破碎和海岸动边界的处理都是近似的，同时引入大量可调参数，增加了数值计算结果的不确定性［6］。此外，这类模型多应用有限差分方法求解，计算过程中容易产生高频数值震荡。为克服这一问题，通常采用数值光滑技术［6-9］。即便较低频率地使用光滑函数，也难以估量其对真正物理现象的影响程度。

结合上述2类模型的优缺点，发展一种适用于海啸波模拟且同时具备2种模型优势的数值模式非常有吸引力。近几年，已经有一些学者开展了这方面研究［10-14］。这些模型均采用早期发展的Boussinesq类方程［15-16］作为控制方程，采用有限体积和有限差分方法进行数值求解。其中，有限体积方法在计算界面通量时均采用一阶精度的通量函数。本文在Kim等拓展的一组适合陡坡地形上的Boussinesq方程［17］基础上，采用具有TVD性质的二阶通量函数算法，建立基于有限体积和有限差分方法的数值模型，模拟孤立波在潜礁上的传播。

1 控制方程

1.1 适合快速变化地形的Boussinesq水波方程

文献［17］给出了一组能考虑快速变化水底地形的Boussinesq水波方程，其一维形式［17］如下:

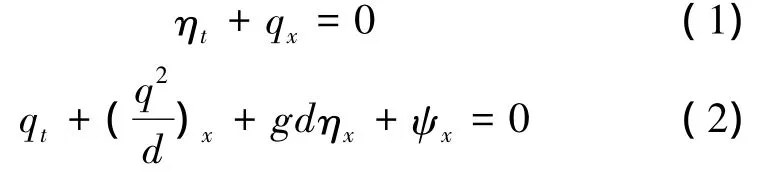
其中，

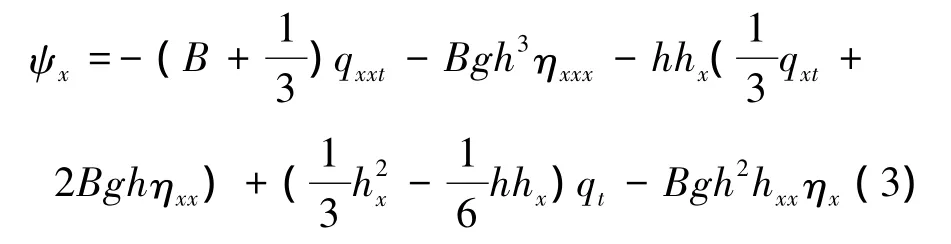
式中:h为静水深，η为波面升高，d=h+η为当地水深，q=du为单位流量(u为水深积分平均流速);下标x和t分别表示变量对空间和时间的导数;B为色散性参数，取值1/15时，控制方程色散性为精确色散关系的Padé［2，2］阶近似，适用于深水波浪传播问题。在上述方程中忽略式(3)中后2项中与底坡坡度有关的项，则可退化为文献［15］给出的方程，高阶地形导数项的存在可以有效提高模型在快速变化地形条件下的精度［17］。

1.2 守恒形式的控制方程

为便于采用有限体积法求解控制方程，将其写为如下守恒形式:

为取得静水平衡解，已将式(2)中dghx改写为［g(h2+2hη)/2］x-ghηx。Sd为色散项，R=-fu|u|代表水底摩擦，f为底摩擦系数，取值在后文给出。

2 数值求解方法

2.1 方程离散

将计算域在时间、空间上做如下离散xi=iΔx(i=1，…，N)，tn=nΔt，在有限体积内［xi-1/2，xi+1/2］×［tn，tn+1］对控制方程(4)进行积分并应用格林定理，可得

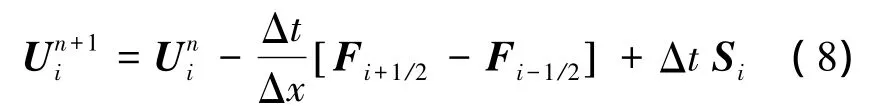
2.2 数值通量计算

图1给出了WAF方法的示意图，其是一种具有二阶精度的Godunov类方法［5］，核心思想在于采用nΔt/2时刻计算界面数值通量，具体表达形式如下

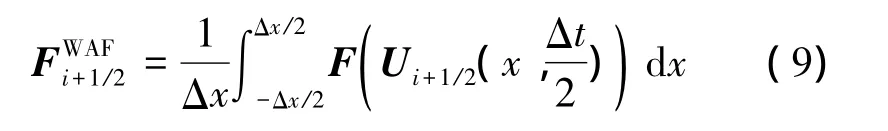
其对应的离散形式为

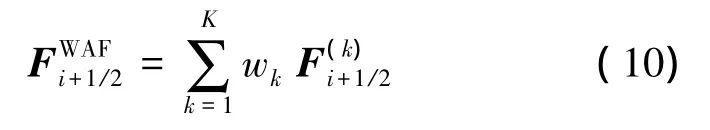
式中，SR和SL分别为左右特征波速度，按照下式计算［5］

式中，“*”号表示中间状态变量，按如下计算［5］

式(10)中wk为各通量分量的权系数［5］，定义为

式中，ck第k个特征波对应的CFL数，由下式给出［5］

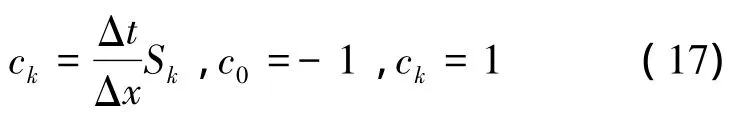
式中，Sk为第k个特征波的波速，见图1、2。

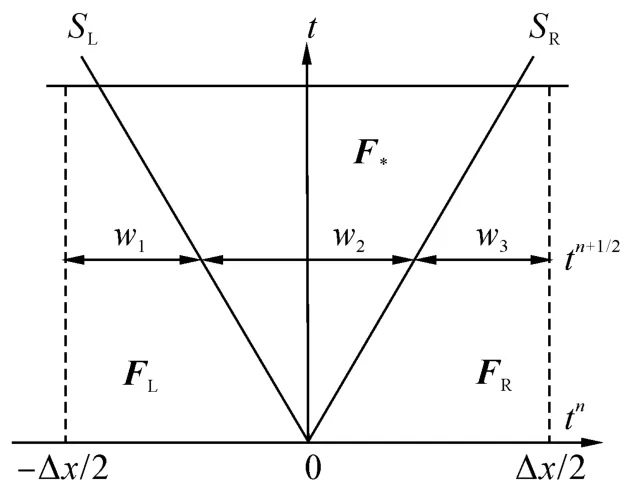
图1 WAF方法示意图Fig.1 The sketch of WAF method

图2 局部黎曼问题示意图Fig.2 The sketch of local Riemann problem

式中，为限制因子，本文取Minmod限制因子［5］。

为提高格式精度，对局部黎曼问题，左右状态变量通过四阶状态插值方法(monotone upstream-centered schemes for conservation laws，MUSCL)［8］进行。

2.3 离散方程的时间积分

时间积分由 MUSCL-Hancock方式［14］进行，该方法为预估校正两步法。其中，预测步为

校正步为利用预测部给出的数值解进行WAF数值通量计算

时间步长的选取则满足如下CFL条件

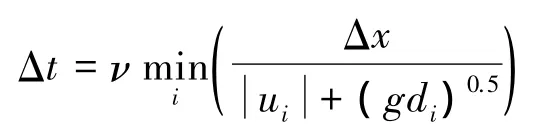
式中，ν取 0.35。

根据人才培养方案及课程标准，希望学生通过本课程学习，能够正确认识舰艇环境因素与人体健康的关系，进一步强化预防为主的理念，了解海军卫生学在海军建设中的重要作用，树立卫生学是维护和提高部队作战（作业）能力的重要保障这一专业信念，掌握发现和解决部队平战时各种卫生学问题必需的基础知识及技能，为今后从事军事医学各个领域的工作，尤其是开展海军卫生学工作打下良好基础。

2.4 边界条件

本文涉及到固壁(完全反射边界)、吸收边界、海岸动边界。

对于固体边界，采用外设3层虚拟网格的方法处理(也考虑到四阶MUSCL方法需要左右3个点网格点值)，即

吸收边界则通过设置海绵层实现，即计算结果乘一光滑函数:

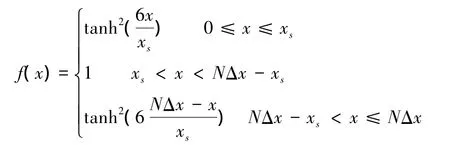
式中，xs为海绵层厚度。

当涉及到海岸动边界问题时，对式(12)、(13)中特征速度进行修正［2，8］:

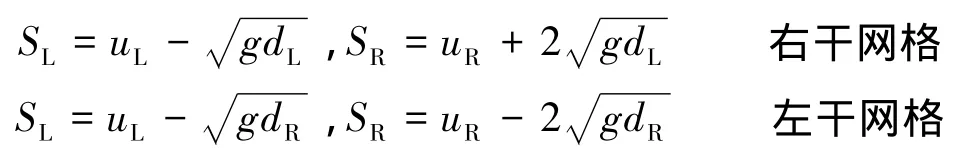
其中，干湿网格的分界定义为水深0.002 m。

根据文献［11］建议，当波面升高同水深比达到0.8时，认为波浪发生破碎，控制方程(1)～(3)中的Boussinesq非线性项和色散性不参与计算，方程退化为浅水非线性方程，波浪破碎处理为激波。

3 计算结果讨论和分析

本节针对所建立数学模型进行验证和应用。数值算例包括常水深水槽中强非线性孤立波的传播和3种代表性潜礁地形上孤立波的传播。数值结果将与解析解或实验数据进行分别对比。

3.1 孤立波在常水深水槽中的传播

数值模拟孤立波在常水深水槽中的传播是检验Boussinesq类数学模型的经典算例［7］。孤立波在传播过程中保持形状和速度不变，这是非线性和色散性相互制约并达到平衡的结果。虽然Boussinesq类模型自身既具有色散性又具有非线性，但若数值格式不合适则会引入额外伪色散或耗散等，从而难以准确模拟孤立波传播过程。

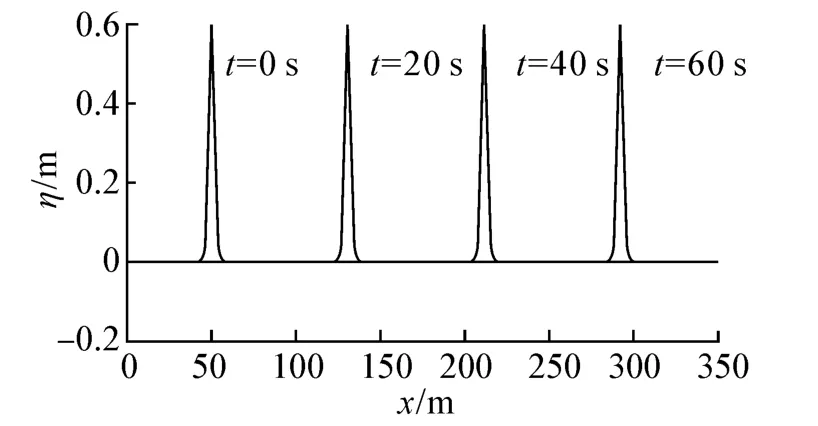
图3 不同时刻孤立波形状数值计算结果Fig.3 The computed solitary wave profile at different moments

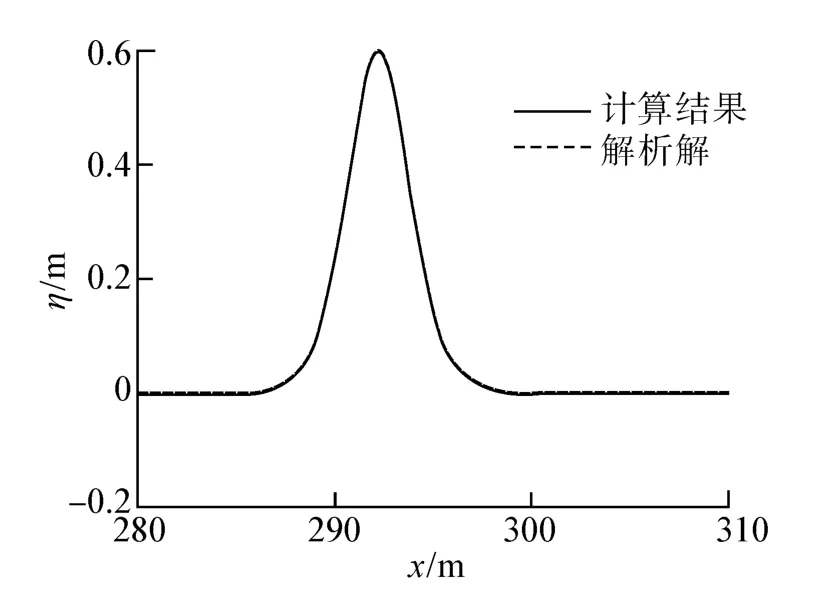
图4 t=60 s时数值计算结果同解析解的对比Fig.4 Comparisons of surface elevation between computed results and analytic solution at t=60 s

数值模拟时，水槽长度375 m，水深h=1.0 m，孤立波波高A=0.6 m，A/h=0.6，属于强非线性波浪。空间网格尺寸Δx=0.05 m，计算时在计算域内给定孤立波解析解(位于x=50 m处)。图3给出了8个不同时刻，孤立波波面的计算结果，可以看出孤立波波形在长时间内保持不变。图4中给出t=70 s时，数值解同解析解的对比，两者几乎重合，这表明孤立波传播速度模拟准确。本算例表明，所建立数值格式有效，可用于模拟孤立波传播问题.

3.2 孤立波在不同潜礁地形上的传播

为了研究海啸波在潜礁地形上的传播特性，Roeber进行了孤立波在不同潜礁地形上的物理模型实验［2］，本节将针对其中的3个典型工况进行模拟，各工况设置和网格尺寸在表1中给出。计算时，底摩擦系数取0.007 5，左侧设置海绵层5 m，右侧为完全反射边界。

表1 各工况设置以及网格尺寸Table 1 Case setting and grid size in simulation

为定量考察计算结果和实验数据的吻合程度，引入 Wilmott因子［18］:

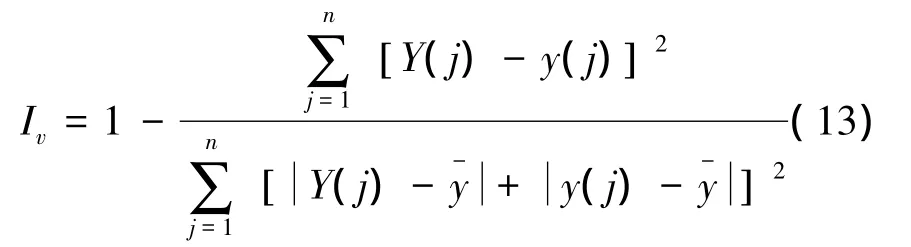
式中，下标v为要考察的变量，Y(j)和y(j)分别为计算和实测数据，为实测数据平均值。当Iv=1时表示两者完全吻合，Iv=0时表示两者不吻合。

工况1的计算结果如图5。该工况中，潜礁初始处于无水状态，因此涉及到动边界的处理，对模型处理干湿边界的能力是一个考验。t＇=52.79，波浪开始在初始干潜礁上传播，在x=22 m处，流体经历从亚临界流速转化为超临界流速状态［2］。t＇=54.79 开始，波浪开始崩塌，波前迅速超前传播，同时一部分反射波浪往相反方向传播，t＇=65.44时刻，由于两部分水体的相反运动，部分潜礁前坡露出水面。总体而言，数值结果同实验数据吻合较好，验证了模型的正确性，尤其是反映出本文模型具有处理干湿动边界问题的能力。同时经计算，其Wilmott因子0.975，这表明数值结果与实验数据吻合度较高。

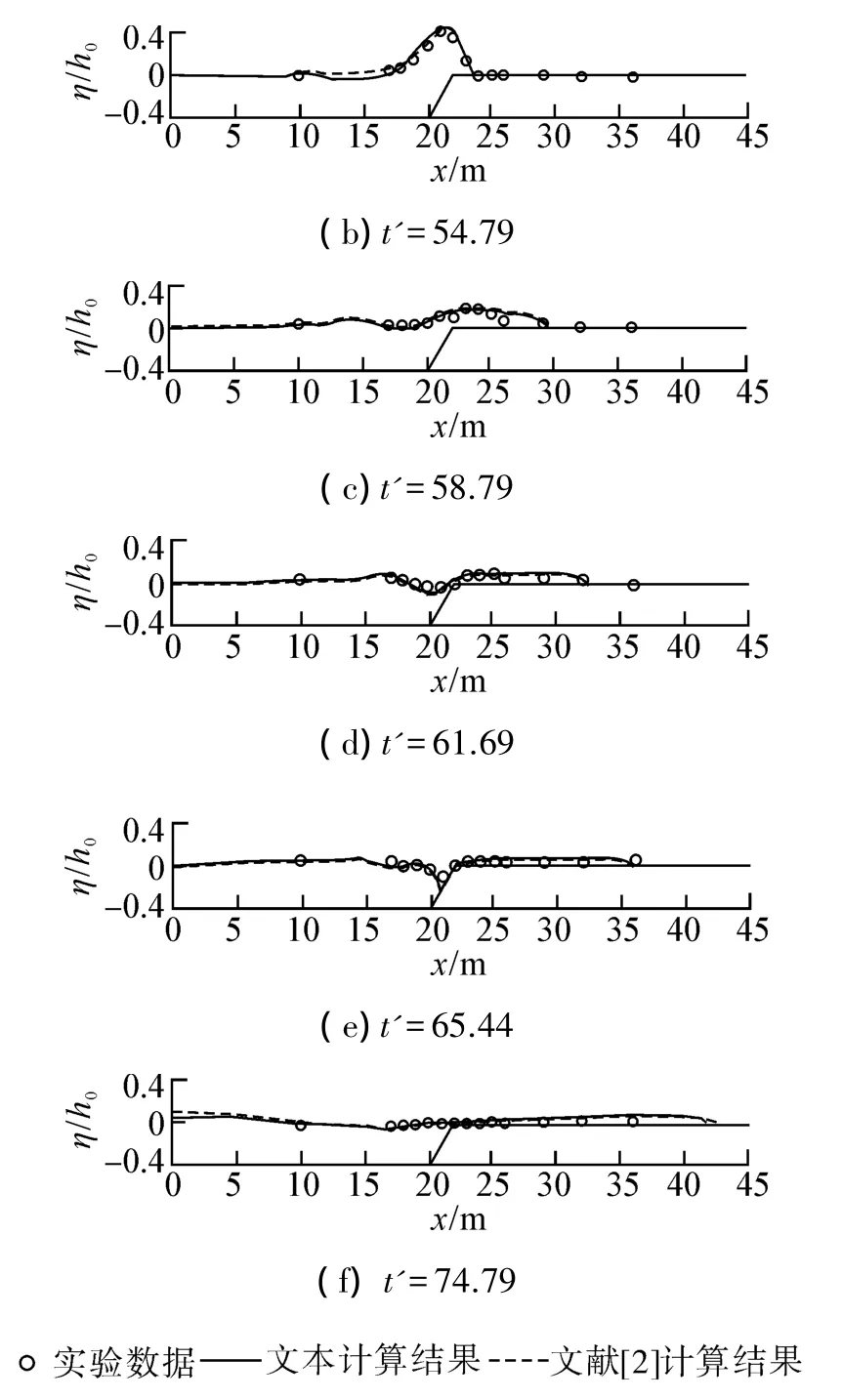
图5 工况1计算波面同实验数据的对比Fig.5 Comparisons of computed and measured surface elevations for case 1

图6给出了工况2的计算结果。与工况1不同，该算例潜礁一直处于淹没状态。t＇=67.1开始，出现激波，即波浪破碎现象。激波形成后一直保持尖锐的形状向前传播，至固壁边界后被完全反射后仍然保持尖锐形状向相反方向传播。t＇=108.5时刻，反射波传入深水，色散性开始发挥作用，波浪分散成不同形态的短波。数值计算结果与实验数据吻合较好，表明模型具有良好的处理激波的能力。该组模拟对应的Wilmott因子为0.965，说明数值结果同实验数据吻合度较高。

工况3在初始时刻潜礁峰露出水面0.06 m，而潜礁平台淹没于水下0.14 m，地形设置类似自然界中带泻湖的潜礁，非常具有代表性。计算结果如图7。可见，孤立波在潜礁前坡传播过程中，波前变陡，破碎发生形成激波。t＇=59.31时刻起，波浪开始跨越潜礁峰传播至泻湖区域。在潜礁峰后激起水跃，并保持尖锐形状向前传播。被完全反射后反向传播，至深水区域由于色散性作用加强也出现诸多短波。数值结果同实验数据吻合良好，表明模型也适用于模拟这种特殊地形条件下孤立波传播和破碎现象。计算得到Wilmott因子为0.942，再次表明模型具有较高的精度。

图6 工况2计算波面同实验数据的对比Fig.6 Comparisons of computed and measured surface elevations for case 2

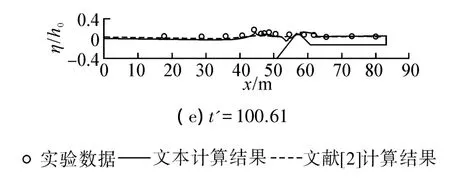
图7 工况3计算波面同实验数据的对比Fig.7 Comparisons of computed and measured surface elevations for case 3

在图5～7中也给出了 Roeber的计算结果［2］，本文计算结果和其较为接近，表明本文模型的数值离散和求解过程正确，也表明色散性Boussinesq类水波方程适用于描述潜礁地形上破碎波传播问题。二者的差别主要由以下2个因素造成:1)模型采用的控制方程不同，Roeber模型建立在Nowgu方程［19］基础上，本文采用Kim给出的方程［17］;2)数值格式不同，Roeber模型采用HLL方法［5］计算通量，采用ABM方法进行时间积分，而本文采用WAF方法计算通量，采用MUSCL-Hancock方式进行时间积分。

4 结论

本文建立了求解Boussinesq水波方程的数值模式，用于模拟具有孤立波形状的海啸波在潜礁地形上的传播、爬坡和破碎过程.得到如下结论:

1)较传统有限差分格式而言，采用有限体积和有限差分混合方法建立的模型，具备数值稳定、捕捉激波、动边界处理简单以及可调参数少的优点，更适用于模拟孤立波在潜礁地形上传播的复杂过程。

2)数值解与解析解和实验数据吻合较好，表明所建立模型具有较高的精度，同时非常适用于潜礁地形上海啸波的数值模拟研究。

3)所建立数值方法也为求解其他Boussinesq方程的数值提供了参考。

［1］YAO Y，HUANG Z H，MONISMITH S G，et al.DH Boussinesq modeling of wave transformation over fringing reefs［J］.Ocean Engineering，2012，47:30-42.

［2］ROBER V.Boussinesq-type model for nearshore wave processes［D］.Honolulu:University of Hawaii at Manoa，2010:47-122.

［3］HUBBARD M E，DODD N.A 2D numerical model of wave runup and overtopping［J］.Coastal Engineering，2002，47:1-26.

［4］LIANG Q，DU G Z.Flood inundation modeling with an adaptive quadtree grid shallow water equation solver［J］.Journal of Hydraulic Engineering，2008，134(1):1603-1610.

［5］TORO E F.Riemann solvers and numerical methods for fluid dynamics:a practical introduction［M］.New York:Springer Press，2009:413-578.

［6］KIRBY J T.Boussinesq models and applications to nearshore wave propagation，surfzone processes and wave-induced currents［M］.New York:Elsevier Science，2002:1-41.

［7］WEI G，KIRBY J T，GRILLI S T，et al.Full nonlinear Boussinesq model for surface waves.I:Highly nonlinear，unsteady waves［J］.Journal of Fluid Mechanics，1995(294):71-92.

［8］SHI F Y，KIRBY J T，HARRIS J C，et al.A higher-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation［J］.Ocean Modelling，2012，43/44:36-51.

［9］LYNETT J.Nearshore wave modeling with higher-order Boussinesq-type equations［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，2006，132:348-357.

［10］ERDURAN K S.Further application of hybrid solution to another form of Boussinesq equations and comparisons［J］.International Journal for Numerical Methods in Fluids，2007，53:827-849.

［11］TONELLI M，PETTI M.Hybrid finite volume-finite difference scheme for 2DH improved Boussinesq equations［J］.Coastal Engineering，2009，56:609-620.

［12］ORSZAGHOVA J，BORTHWICK AGL，TAYLOR P H，et al.From the paddle to the beach-A Boussinesq shallow water numerical wave tank based on Madsen and S∅rensen’s equations［J］.Journal of Computational Physics，2011，231:328-344.

［13］CIENFUEGOS R.A fourth-order compact finite volume scheme for fully nonlinear and weakly dispersive Boussinesq-type equations.Part II:Boundary conditions and validation［J］.International Journal for Numerical Methods in Fluids，2007，53:1423-1455.

［14］SHIACH J B，MINGHAM C G.A temporally second-order accurate Godunov-type scheme for solving the extended Boussinesq equations［J］.Coastal Engineering，2009，56:32-45.

［15］MADSEN P A，SORENSEN O R.A new form of the Boussinesq equations with improved linear dispersion characteristics，Part 2.A slowly-varying bathymetry［J］.Coastal Engineering，1992，18:183-204.

［16］NWOGU O.An alternative form of the Boussinesq equations for near shore wave propagation ［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，1993，119(6):618-638.

［17］KIM G，LEE C，SUH K D.Extended Boussinesq equations for rapidly varying topography［J］.Ocean Engineering，2009，36:842-851.

［18］WILMOTT C J.On the validation of models［J］.Physical Geograhpy，1981，2:184-194.

［19］NWOGU O.An alternative form of the Boussinesq equations for nearshore wave propagation［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，1993，119(6):618-638.