大件运输中简支梁桥的动力响应分析及监测

刘波，王有志，王涛，丛侃，徐永芝

(1.山东大学 土建与水利学院，山东 济南250061;2.长安大学 公路学院，陕西 西安710064)

中国加入WTO以来，公路大件运输日趋频繁，经由公路运输的重型工业设备(如发电机静子、变压器及反应器等)重量不断刷新记录。繁重的大件运输任务，对公路桥梁的承载能力和安全评估提出了挑战。目前针对超重大件过桥的研究多集中于桥梁的承载能力评估、临时加固措施方面［1-3］，针对大件过桥时车桥耦合振动响应的研究则较少。

大件运输时一般需要对车辆所经过的桥梁进行临时加固或补强，基于经济性考虑遴选的运输路线上鲜有大跨径桥梁，往往中小跨径桥梁占绝大多数。大件过桥时往往需要暂时中断交通，禁止其余车辆、行人通过，为降低桥梁的动力响应要求大件运输车辆以低速过桥。实际上，以“重车轻桥”、“长车短桥”为特征的大件运输车桥耦合系统有其独特的动力特性，一味地要求运输车辆降低速度过桥往往并不现实，在很多情况下也没有必要。

通过对车桥耦合系统的分析，本文把车桥系统分解成2个独立的运动体系，即桥梁振动子系统和车辆振动子系统，利用车轮和桥面的位移协调方程来考虑车桥的接触［4］。同时，以九龙河中桥为工程实例，利用ANSYS中APDL语言编写车桥耦合振动分析程序，采用梁格法建立初始有限元模型。结合大件过桥时桥梁的动力响应监测数据，对车桥耦合系统的刚度、阻尼等参数进行反演，并对大件过桥时桥梁的动力学特性进行了分析和研究。

1 车桥耦合体系振动模型

研究车桥系统动力相互作用的经典方法有匀速移动常量力模型、匀速移动简谐力模型、匀速滚动质量模型、匀速移动弹簧-质量模型等，在简支梁强迫振动微分方程的基础上，利用振型叠加法和振型的正交性推导出车桥系统的动力平衡方程。实际上，车辆由刚性底盘(车身)、悬架、轮胎等元件组成，各元件在空间具有浮沉、伸缩、侧滑、俯仰、横摆、侧倾6个自由度(3个平动和3个转动)，它们之间通过线性或非线性的各种阻尼器和弹簧元件连接。现代车桥耦合振动研究将汽车悬架、轮胎模拟为线性弹簧和阻尼器，考虑刚性车身的浮沉、伸缩、侧滑、俯仰、横摆、侧倾6个自由度，研究车桥的竖向、横向耦合振动［5］。本文针对斜桥结构的特性，建立空间整车模型，应用广义虚功原理和有限元法推导了车辆振动子系统和桥梁振动子系统的振动方程组，然后通过位移协调方程来实现求解。

1.1 空间整体车辆模型

威海化工机械厂制造的土库曼斯坦化工厂吸收塔每台净重488.1 t，选用4轴式牵引车+3纵25轴平板挂车+助力车运输，装载后平板挂车总重600.6 t，如图1、2所示。车辆之间采用拖曳式联接装置，其主要承受纵向荷载，竖向荷载仅为联接装置的自重，由于主要关注车桥耦合系统的竖向振动，牵引车、平板挂车、助力车作为独立车辆考虑。

由于车辆竖向与横向振动之间的耦合效应较弱，为计算简便，将车辆竖向与横向振动分开进行，只考虑车体、悬架与轮胎的浮沉、俯仰自由度。简化为二系的弹簧-质量-阻尼系统空间整体车辆模型如图3所示，4轴牵引车包含8个端点11个自由度，3纵25轴平板挂车包含75个端点78个自由度，3轴助力车包含6个端点9个自由度。图中:M为车体质量，3个自由度分别为竖向位移Z0、绕横轴的旋转自由度θ和绕纵轴的旋转自由度φ;mi为构架质量与轮对质量之和，每个块质量被赋予了1个竖向位移自由度Zi;Kui为二系竖向刚度;Cui为二系竖向阻尼;Kdi为一系竖向刚度;Cdi为一系竖向阻尼;i=1，2，…，N;对于牵引车辆，N=8，对于平板挂车，N=75，对于助力车，N=6;L、L1～L4表示车辆各轴及质心之间的纵向距离，B表示车体外侧轮对间的横向距离。

图1 大件运输夜间过桥Fig.1 oversize transport during night

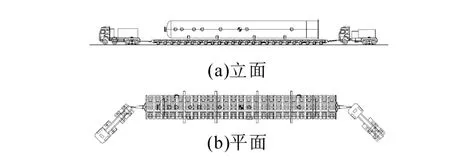
图2 大件运输车辆荷载简图Fig.2 Vehicle load for oversize transport

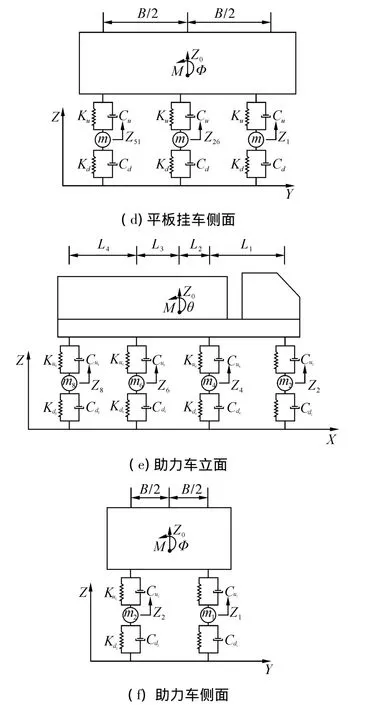
图3 车辆简化模型Fig.3 Simplified vehicle model

以车辆静力平衡位置为起始点，在俯仰角θ和侧倾角φ较小的情况下，车身第N个端点竖向位移方程为

由广义虚功原理［6］得

式中:δZ0、δZi、δθ、δφ 为车辆广义虚位移，不为零;δZgi为桥梁广义虚位移，相对车辆而言假设为零。

将式(1)代入式(2)，令广义虚位移对应系数项为零，可得到如下方程:

车身质心竖向运动方程:

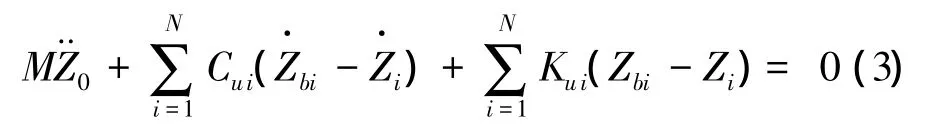
车身俯仰运动方程:

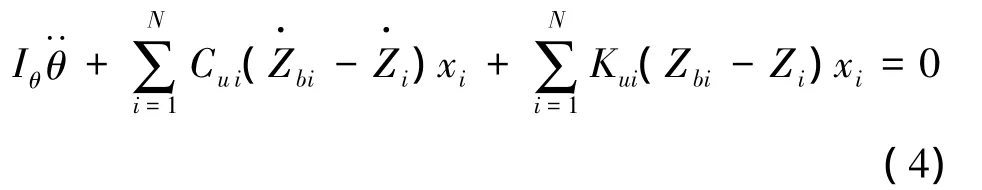
车身侧倾运动方程:

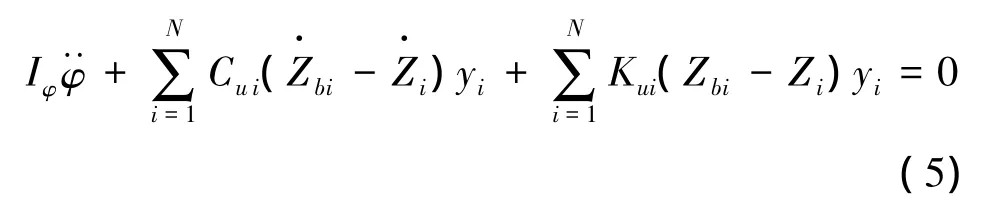
车轮竖向运动方程:

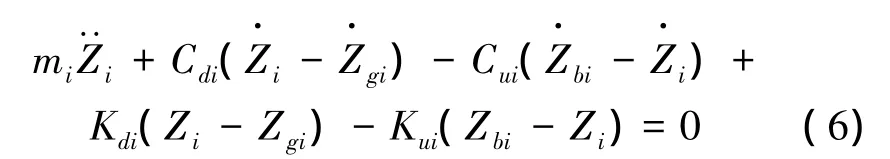
式中:xi、yi表示车轮的平面坐标。

将上述各式整理写成矩阵形式得

式中:Mv、Cv、Kv分别表示车辆振动系统的质量矩阵、阻尼矩阵和刚度矩阵，Fv(t)表示激振力列向量，(t)、(t)、uv(t)分别表示车辆振动系统的加速度、速度、位移列向量。

1.2 桥梁振动方程

采用梁格法建立空间有限元模型，桥梁结构的运动方程为

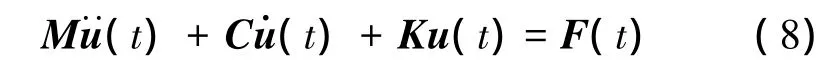
1.3 车桥耦合系统的位移协调条件

假设车轮在运行的过程中始终与桥面密贴不脱离，即得车桥耦合振动系统的位移协调条件如下

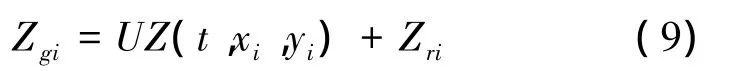
式中:UZ(t，xi，yi)表示车轮i对应桥梁节点的挠度，向下为负;Zri表示桥面上点的不平整度，向下为负。

根据车辆与桥梁接触点间相互作用力的平衡关系，可得第i个车轮对桥梁结构的作用力如下

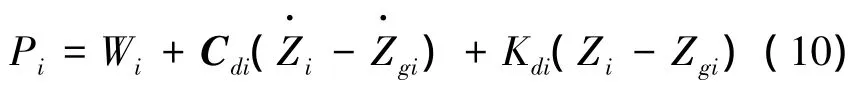
式中:Wi表示车辆静止时车体分配到第i个车轮的重力与该轮自重之和，向下为负。

1.4 车桥耦合振动数值求解

车桥耦合系统振动方程为二阶变系数微分方程组，荷载项均为时变函数，解此类方程大多采用直接积分法。本文采用Newmark-β隐式积分法进行数值求解，步骤如下:

1)建立桥梁模型，形成桥梁子系统质量矩阵、刚度矩阵、阻尼矩阵;

2)输入车辆参数，形成车辆子系统质量矩阵、刚度矩阵、阻尼矩阵;

3)假定车桥耦合振动系统的初始状态;

4)根据桥梁子系统的位移、速度及桥面不平整度确定桥梁子系统对车辆子系统的反作用力，形成式(7)荷载向量;

5)利用Newmark-β数值迭代法求解车辆子系统振动微分方程组，求出车辆子系统位移向量、速度向量、加速度向量;

6)计算车辆子系统对桥梁子系统的作用力，求解桥梁子系统振动微分方程组;

7)判断平衡迭代收敛情况，若满足收敛条件，则停止迭代。

2 实测桥面不平度与功率谱估计

桥面不平顺是车桥耦合振动的主要激励因素之一，按照功率谱密度可将路面不平度分为A～H共8级。为定量评价桥面不平度对车桥耦合系统动力响应的影响，需对实测桥面不平度进行功率谱估计和平度分级。传统的功率谱估计方法通常直接或间接对有限个样本数据进行傅里叶变换得到功率谱，其存在分辨率低、方差性能不好等缺点。基于AR模型的现代功率谱估计可以通过求解线性方程组得到模型参数的精确估计，进而可以求得精确的功率谱估计。

图4所示为九龙河中桥实测的桥面不平度，采样间距为30 cm，图5为利用AR模型求解得到的桥面不平度功率谱，实测样本的功率谱位于路面平度分级B区。

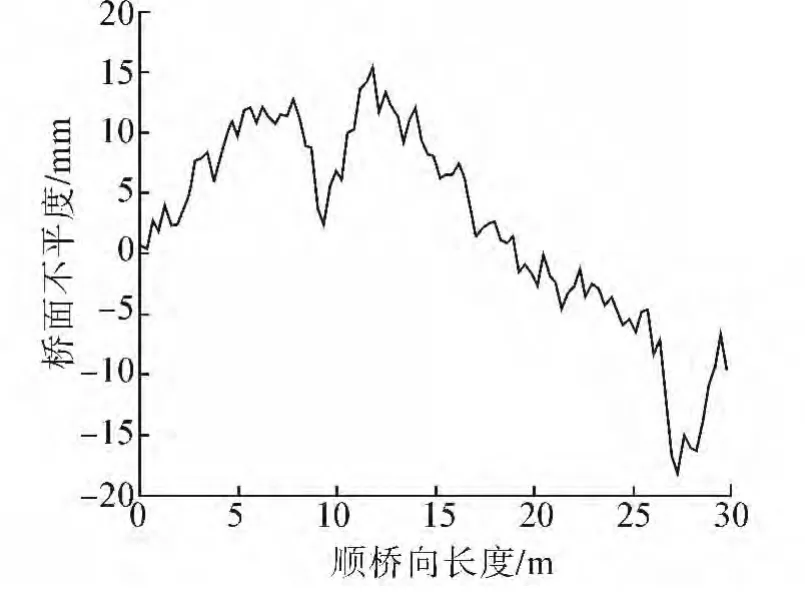
图4 实测桥面不平度Fig.4 Measured deck roughness

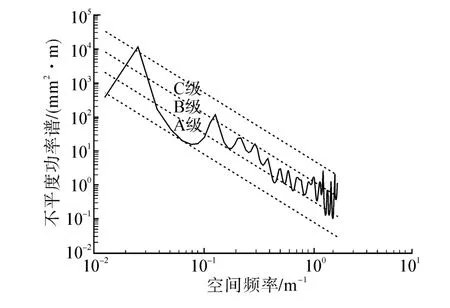
图5 实测桥面不平度功率谱Fig.5 Measured deck roughness power spectrum

3 车桥耦合振动参数反演

车桥耦合振动分析面临的一个主要问题是车桥振动系统的参数难以确定，而正分析的复杂性使得传统反分析方法面临着很大的挑战，而基于改进的支持向量回归机v-SVR的反分析方法能够在少而精的正分析基础上结合实测数据快速反馈出数值计算参数，是目前工程反分析研究领域一个很重要的研究方向［7］。

3.1 v-SVR 算法原理

回归问题即寻找从输入空间到输出空间的一个映射f:Rn→Rl，使得f(x)=y。v-SVR的目标是寻求回归函数［8］:

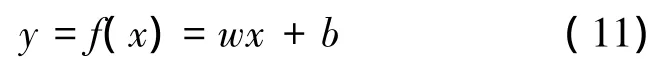
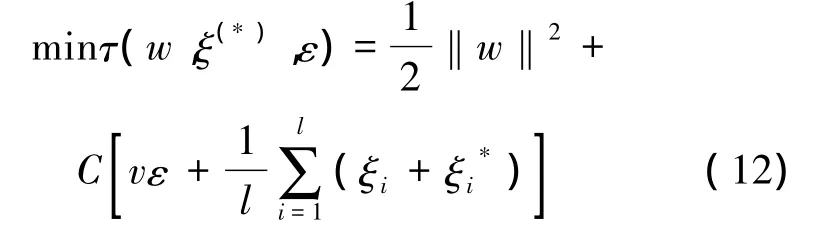
式中:C为用来平衡模型复杂性项和训练误差项的权重系数，ε为不敏感损失函数，ξ、ξ*为松弛因子。式(12)的对偶形式为

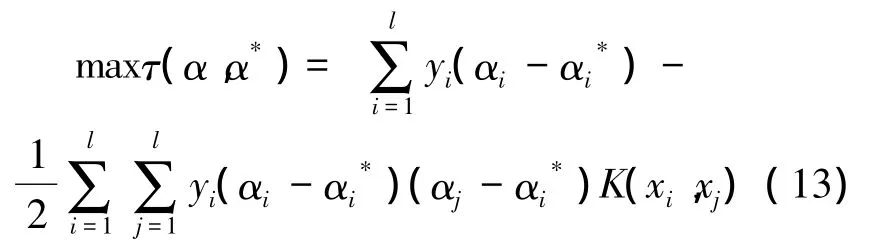
通过求解式(12)、(13)，即可得到通过学习训练得到的回归函数为

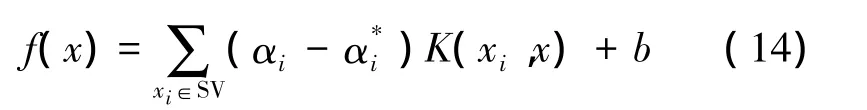
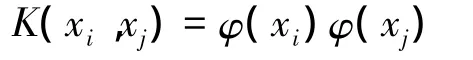
式中:αi为拉格朗日系数;SV为支持向量的集合为核函数，常用的有P阶多项式、高斯径向基核、多层感知器sigmoid核和样条核函数等。

3.2 预测回归模型的建立及参数反演

在对九龙河中桥挠度监测的基础上，建立反分析目标函数如下:

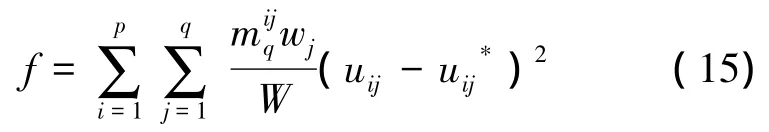
式中:uij表示第i块板实测挠度时程曲线第j个特征点的挠度，表示uij对应的理论计算值，表示车辆荷载的横向分布系数，wj表示第j个特征点对应主要车辆的重量，W表示车队的总重。

通过对车桥耦合振动问题的分析，确定车桥系统待反演13个参数的取值范围，确认反演构造样本如表1所示。同时，采用正交设计表L27(313)给出训练的学习样本，对于每一种试验组合，ANSYS进行正向计算，找出对应的监测点竖向位移值，根据式(15)计算目标函数值，将与其对应的待反演参数组合成一个学习样本，共得到27个训练样本。

参数回归反演首先要根据训练样本建立回归预测模型［9］，本文采用留一法设计预测模型，采用网格搜索法搜索最优计算参数。最优参数对应的支持向量机即为可用于反分析的关于待反演参数与监测位移的表面响应模型。通过适当扩大待反演参数的搜索范围和密度，令目标函数取极小值得到13个参数的反演结果如表2所示。

表1 反演样本构造Table l Constructed samples for back-analysis

表2 参数反演结果Table 2 Parameter from back-analysis

4 动力响应分析

4.1 跨中挠度理论与实测结果对比

九龙河中桥宽40 m，跨径布置为5 m×10 m，斜交角67°，上部结构为简支空心板。大件过桥时严格按照划定的车道低速(6.2 km/h)均匀行驶，采用DEWE-3010多通道动态数据采集系统和机电百分表监控首跨空心板的跨中挠度，测点编号1～7，如图6所示，其中P表示轴重。在车桥耦合振动参数反演的基础上，将表2中的参数代入正分析程序可得跨中挠度的理论和实测时程对比曲线如图7所示。

图6 动挠度测点横向布置示意图Fig.6 Transverse arrangement of measuring points

图7 跨中挠度理论和实测时程曲线图Fig.7 Theoretical and measured deflection time-history curve

从图7可以看出，跨中挠度的理论计算值和实测值基本吻合。4#板受力最大，跨中最大挠度理论值为2.515 mm，与实测值 2.525 mm 相差约 0.4%;利用v-SVR预测回归模型得到的跨中最大挠度预测值为2.584 mm，与实测值相差约2.3%。图7挠度时程曲线出现3个大的波峰f1、f2、f3，f1表示牵引车引起的跨中挠度极值;f2呈平台状，表示平板挂车车轮持续满跨布置时引起的跨中挠度峰值区间;f3表示助力车引起的跨中挠度极值。挠度时程曲线f2平台相对比较平稳，但是也存在明显的波动，这主要是由于桥面不平度引起的，不同的桥面不平度产生不同的波形。

4.2 速度和加速度

图8表示跨中截面竖向速度、加速度时程曲线，由图中可以看出，对应于挠度曲线平台段的空心板跨中截面竖向速度和加速度受到明显抑制，曲线呈“哑铃型”，这是由于平板挂车车轮持续满跨布置所引起的，这也是“长车短桥”车桥耦合振动系统的显著特征。当挂车长度大于桥梁跨度时，平板挂车对桥梁来说既是荷载又是约束，两者耦合振动作用明显。

图8 跨中截面动力响应时程曲线Fig.8 Time-history curve of dynamic response

4.3 冲击系数

行驶在公路桥梁上的汽车车辆因受到多种复杂因素的影响，对桥梁产生的动力效应往往会大于其静止作用在桥上所产生的静力效应，称之为车辆的冲击效应。车辆的冲击效应一般用冲击系数定义如下:

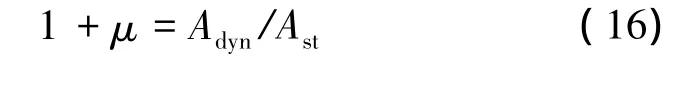
式中:Adyn为车辆荷载过桥时桥梁跨中动态挠度的峰值;Ast为同一车辆荷载静力作用时跨中挠度的最大值。目前我国规范在桥梁结构的冲击系数计算中仅仅考虑了结构的基频。实际上冲击系数不仅与结构的基频有关，还与桥面不平度、车辆行驶速度、车辆自身各部分之间的连接刚度和阻尼等参数密切相关。

根据式(16)，当大件运输车辆以6.2 km/h的低速度过桥时，冲击系数实测值为0.119，虽然低于文献［10］计算值 0.388(基频为 9.83 Hz)，但是仍然不可忽视。这打破了以往的认识，意味着在进行大件过桥承载力评估时即使运输车辆以低速过桥也必须考虑车辆荷载的冲击效应。

在实测桥面不平度激励下，对不同车速下 (5～40 km/h)桥梁的动力响应进行计算后发现，冲击系数的变化范围为0.118～0.124，车速对冲击系数的影响较小。

我国的道路路面不平度基本属于A～C级，将路面功率谱进行快速傅里叶逆变换［11］即可重构路面不平度样本。图9为B级路面不平度重构样本，图10表示不同路面等级、不同车速下的冲击系数。可以看出，车速的变化对冲击系数的影响同样较小且并无明确的变化规律［12］，而路面不平度对冲击系数的影响较大。路面极平时可以不考虑车辆的冲击系数，A～C级路面的冲击系数分别为 0.041～0.064、0.105～0.126、0.221～0.254。

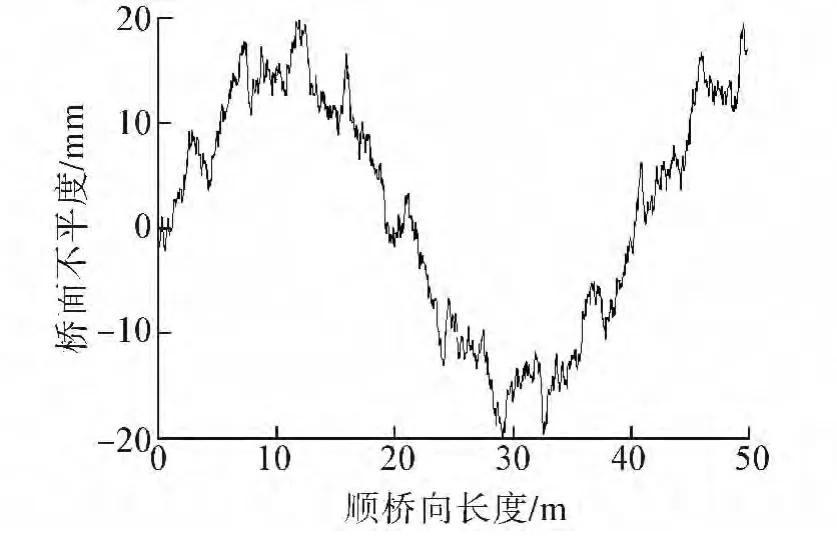
图9 B级路面不平度Fig.9 Class B road roughness

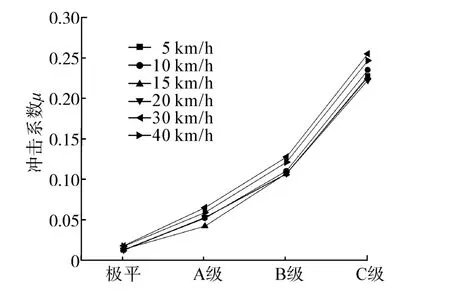
图10 不同路面等级、不同车速下的冲击系数Fig.10 Impact factor under different road roughness and speed

5 结论

1)对大件运输时桥梁结构的动力响应进行了理论分析和实桥监测，理论值和实测值吻合较好。

2)外运大件以6.2 km/h的低速通过桥面不平度为B级的简支梁桥时，其实测冲击系数仍然达到0.119。在对大件过桥进行安全评估时，即使运输车辆以低速通过，也应考虑车辆荷载的冲击作用。

3)大件过桥时，对于中小跨径桥梁，车速对于冲击系数的影响较小，路面不平度对于冲击系数的影响较大。在满足交通安全的前提下，不应过度限制运输车辆的速度，对桥面进行平整度处理是降低车辆冲击效应的有效方法。

4)挠度时程曲线峰值平台、“哑铃型”的速度和加速度时程曲线为“长车短桥”耦合振动系统的显著特征，平板挂车对桥梁来说既是荷载又是约束，两者耦合振动作用明显。

5)正交试验和支持向量回归机v-SVR的结合显著提高了参数反演的效率，基于v-SVR预测模型的精度能够满足工程需要。

［1］邢文榜.大件运输中桥梁通过性快速评定方法研究［J］.中外公路，2011，31(3):217-220.XING Wenbang.Rapid assessment method research on bridge during oversize transport［J］.Journal of China ＆ Foreign Highway，2011，31(3):217-220.

［2］刘尧，叶贵如，张治成.桥上桥在大件运输中的应用研究［J］.武汉理工大学学报:交通科学与工程版，2008，32(1):176-179.LIU Yao，YE Guiru，ZHANG Zhicheng.Method"bridge on the bridge"used in the massive product transportantion［J］.Journal of Wuhan University of Technology:Transportation Science＆ Engineering，2008，32(1):176-179.

［3］钱鸿，蒙云，张会礼，等.大件运输中桥上桥的特殊用法与工程实践［J］.重庆交通学院学报，2005，24(5):10-13.QIAN Hong，MENG Yun，ZHANG Huili，et al.A special application of temporary steel bridge in heavy-cargo transportation［J］.Journal of Chongqing Jiaotong University，2005，24(5):10-13.

［4］施颖，宋一凡，孙慧，等.基于ANSYS的公路复杂桥梁车桥耦合动力分析方法［J］.天津大学学报，2010，43(6):537-543.SHI Ying，SONG Yifan，SUN Hui，et al.Dynamic analysis method of vehicle-bridge coupling for complicated bridges based on ANSYS［J］.Journal of Tianjin University，2010，43(6):537-543.

［5］李小珍，张黎明，张洁.公路桥梁与车辆耦合振动研究现状与发展趋势［J］.工程力学，2008，25(3):230-240.LI Xiaozhen，ZHANG Liming，ZHANG Jie.State-of-the-art review and trend of studies on coupling vibration for vehicle and highway bridge system［J］.Engineering Mechanics，2008，25(3):230-240.

［6］曾庆元.弹性系统动力学总势能不变值原理［J］.华中理工大学学报，2000，28(1):1-3.ZENG Qingyuan.The principle of total potential energy with stationary value in elastic system dynamics［J］.Journal of Huazhong University of Science and Technology，2000，28(1):1-3.

［7］邢万波，周钟，唐忠敏，等.基于v-SVR和改进PSO算法的反分析方法及应用［J］.岩土力学，2009，30(增 2):540-546.XING Wangbo，ZHOU Zhong，TANG Zhongmin，et al.A new back-analysis method based on ν-SVR and improved PSO algorithm and its application［J］.Rock and Soil Mechanics，2009，30(Suppl 2):540-546.

［8］SCHOLKOPF B，SMOLA A，WILLIAMSON R，et a1.New support vector algorithms［J］.Neural Computation，2000(12):1207-1245.

［9］CHANG C C，LIN C J.LIBSVM:A library for support vector machine［R］.Taiwan:National Taiwan University，2001:5.

［10］JTG D60—2004.公路桥涵设计通用规范［S］.北京:人民交通出版社，2004:26.

［11］刘献栋，邓志党，高峰.基于逆变换的路面不平度仿真研究［J］.中国公路学报，2005，18(1):122-126.LIU Xiandong，DENG Zhidang，GAO Feng.Study of simulation of road roughness based on inverse transform［J］.China Journal of Highway and Transport，2005，18(1):122-126.

［12］谭国金，刘寒冰，程永春，等.基于车-桥耦合振动的简支梁桥冲击效应［J］.吉林大学学报:工学版，2011，41(1):62-67.TAN Guojin，LIU Hanbing，CHENG Yongchun，et al.Analysis of impact of vehicle to simply supported beam［J］.Journal of Jilin University:Engineering and Technology Edition，2011，41(1):62-67.