基于深度差的离群点识别与修正方法

李 嘉,林 欢,蓝秋萍,马符讯

(河海大学，地球科学与工程学院，江苏 南京 210098)

基于深度差的离群点识别与修正方法

李 嘉,林 欢,蓝秋萍,马符讯

(河海大学，地球科学与工程学院，江苏 南京 210098)

离群点的存在会给点云后续处理与应用带来干扰，文中针对扫描过程中快速通过的车辆或行人造成的离群点提出基于深度差的识别与修正方法。分析此类离群点的产生机理，并运用基于球面投影的点云构网方法构建点云的拓扑关系，在此基础上提出根据深度差识别离群点的方法以及兼顾不同点云质量的阈值自动选择方法；设计了基于二次曲面拟合的点云修复方法；利用真实隧道数据进行实验，实验结果验证了文中方法的有效性和稳定性。

离群点；三角构网；测距异常；二次曲面拟合；插值

三维激光扫描系统已经广泛应用于已建成并投入运营的高速公路桥梁和隧道的三维重建与变形检测中，扫描过程中快速经过的车辆和行人会在扫描点云中留下“断续”、“跳跃”的粗差点，也被称为离群点[1]。本文提出的离群点识别及修正方法只针对扫描过程中车辆和行人遮挡造成的这类离群点，所以后文提到的离群点特指此类离群点。如图1所示为三维激光扫描仪扫描的隧道点云，隧道内杂乱的点即为快速通过车辆造成的离群点。三维激光扫描仪是按照倒“Z” 字形的顺序扫描[2]，快速通行的车辆会对扫描目标产生临时遮挡，阻碍激光光束到达实际扫描物体表面，从而在移动车辆位置产生离群点，并造成被遮挡目标表面的数据缺失。经分析离群点具有如下特性：

1)离群点与相应物体表面缺失点在同一视线方向，即两者的水平角值和竖直角值相等，只是深度值大小不同；

2)离群点的大部分顺序扫描邻近点都在扫描物体表面，离群点与它们的距离较大。

由上述两特性可以看出，离群点的测距值存在显著误差，针对离群点的识别问题，Knorr和Raymond提出了一种基于距离的检测方法[3]，该方法是根据一个点与其邻近点的距离来判断该点是不是离群点，对于均匀点云处理效果较好，但对于密度存在变化的点云可能产生误判。Breunig设计了LOF(局部离群系数)及基于密度的检测方法[4]，该方法能处理一般的散乱点云数据，但需事先给定离群点的密度估计，对于那些密度大于给定值的离群点则无法被识别。

图1 隧道点云

本文在分析上述方法的基础上不仅设计了离群点的识别方法，而且设计了点云修复方法。将点云进行以测站中心为原点的球面投影，并基于水平角、竖直角建立点间拓扑关系。根据相对邻近点的测距值差异显著性识别离群点[5]。基于曲面二阶连续性改正离群点测距值，从而完成点云修复。利用真实高速公路隧道扫描数据验证了离群点识别方法的有效性，并利用仿真实验论证了离群点修正算法的准确性。

1 基于球面投影的三维点云三角构网

三维点云的三角网构建算法种类繁多，本文采用了张帆提出的基于球面投影的单站地面激光扫描点云构网方法[6]。首先利用中心投影将单测站点云投影到以测站中心为球心的球面上，然后根据球面投影点的水平、竖直角实施扫描点的构网，从而完成单测站三维点云在欧氏空间下的三角构网[7]。图2(a)所示为墙面点云数据,对墙面点云三角构网后得到图2(b)。

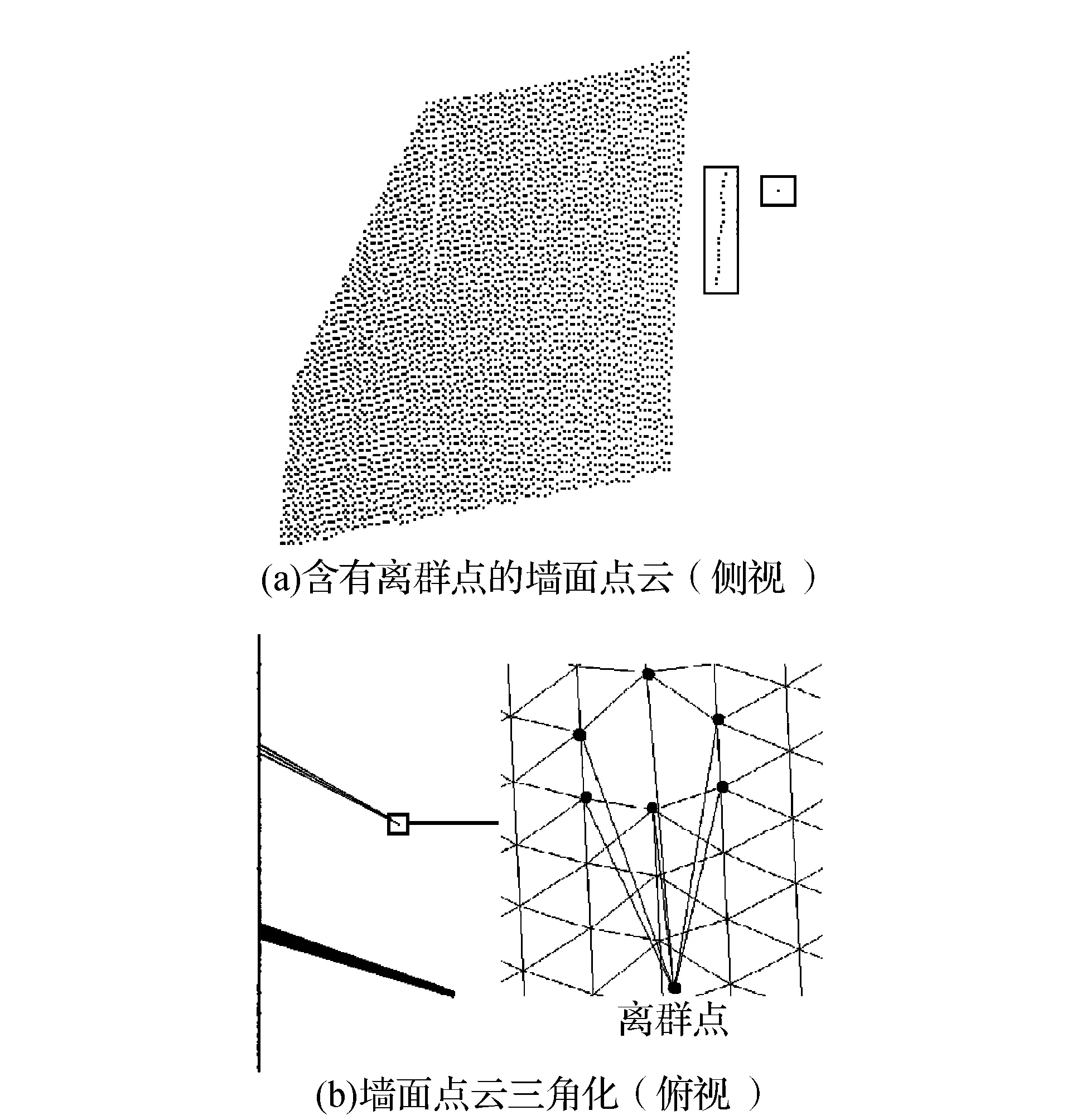
图2 墙面点云

2 离群点的识别

图2(a)为含有离群点的墙面点云数据，其中矩形框内的点即为离群点。对该点云应用前述三角化方法之后得到如图2(b)所示的墙面三角表面网及局部放大示意图，图中离群点与其邻近点所构成的三角形为狭长三角形，其中狭长边(即包含离群点的三角边)与激光飞行方向大致相似，说明离群点与其邻近点具有较大的深度差。基于该特性，本文按照如下思路设计了识别离群点的算法：首先计算每个点与其邻近点的深度值之差，然后选择出合适的阈值，最后根据阈值识别离群点。

2.1 深度差计算

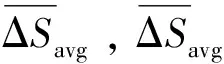
(1)

(2)

2.2 选择阈值识别离群点

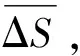
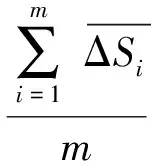
(3)

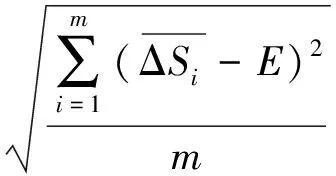
(4)

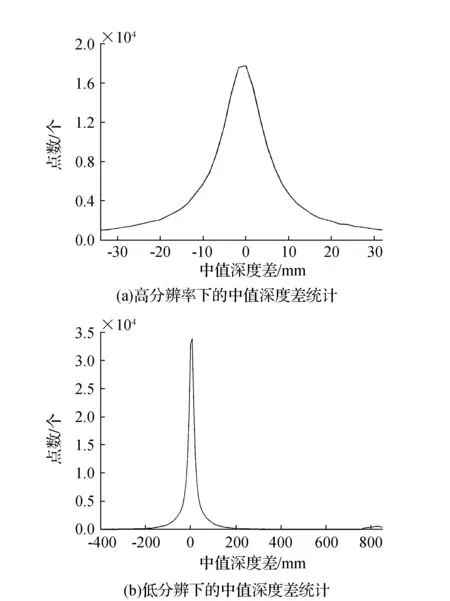
图3 中值深度差统计

三维激光扫描是一种针对三维物体表面的连续密集采样，相邻采样点的间距较小，相邻点之间的测距深度变化值也较小。通过对多种人工建筑表面三维激光扫描点云的统计分析，发现相邻激光测点的平均深度差都与所采用扫描仪的单点测距误差值大小相当，即：单点激光测距的随机误差是相邻点之间深度差异的主要成分。因此，在高密度扫描条件下，实际落在物体表面上的邻近点之间的测距深度差具有与单点激光测距误差相一致的正态统计分布规律，而远离物体表面的飞点则相当于测距粗差点，在如图3所示的直方图统计中表现为远离期望中心的异常分布。根据正态分布曲线的性质可知，正常的情况下，中值深度差在(E-σ,E+σ)区间的点数有68.25%(其中E和σ分别代表期望和标准差，可由式(3)、式(4)计算得到)；在(E-2σ,E+2σ)区间的点数有85.45%；在(E-3σ,E+3σ)区间的点数有99.73%。即：对于目标表面的正常扫描点而言，其中值深度差大于E+3σ的点出现的概率是接近于0的小概率事件，而远离目标表面的飞点与邻近点的深度差则显著大于E+3σ。所以本文选择E+3σ作为初步识别候选离群点的阈值。由于这种方法可能会将一些阶跃边缘点识别出来，所以又针对候选离群点设计了进一步精确确认的方法。

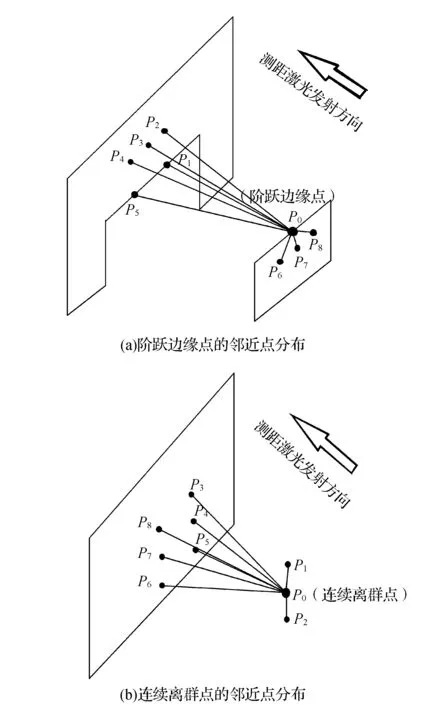
图4 阶跃边缘点与连续的邻近点分布对比

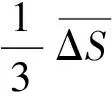
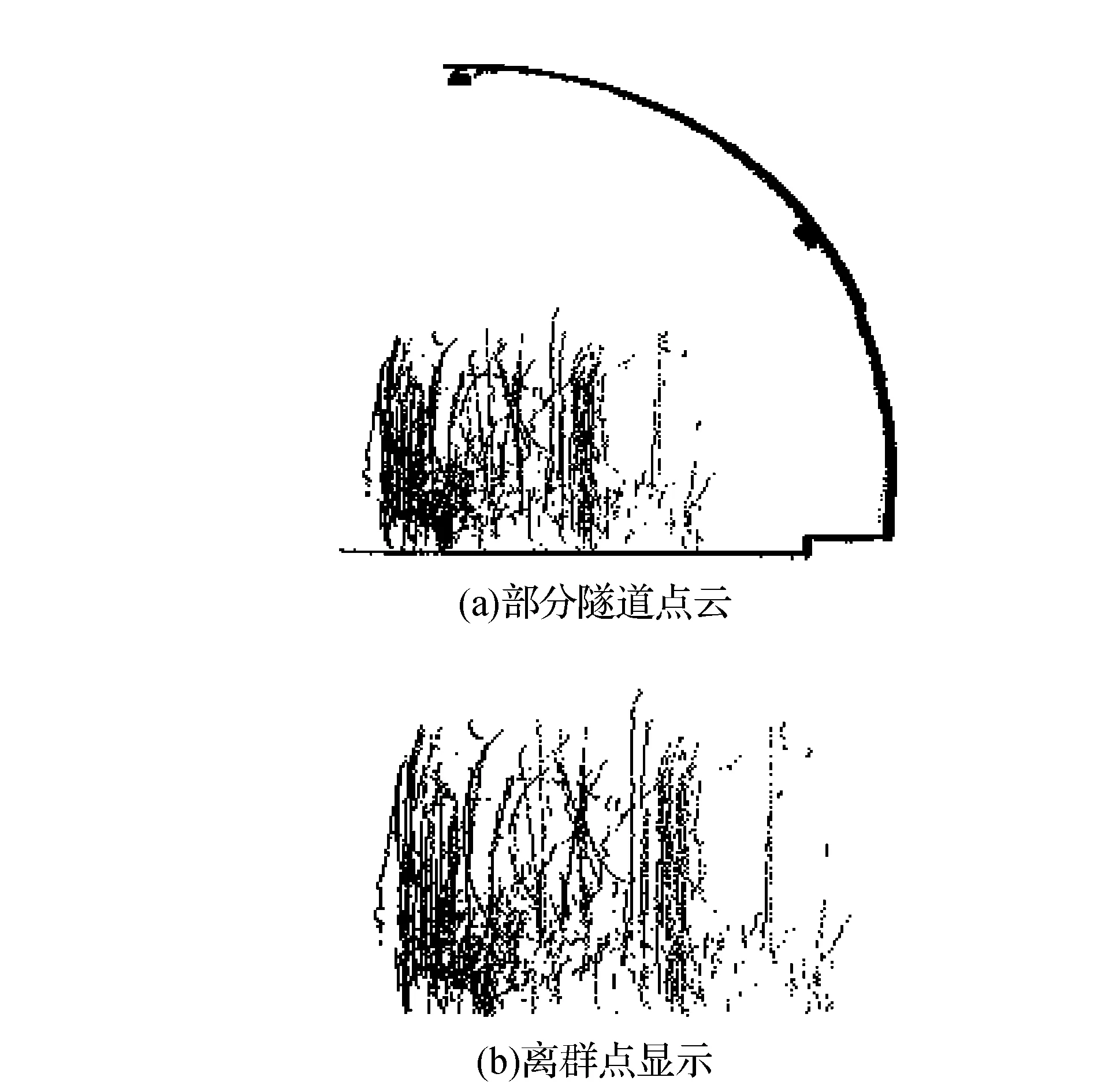
图5 隧道点云

3 离群点的修正

由于离群点与相应表面缺失点的水平角值和竖直角值相等，只是深度值大小不同，所以可以根据邻近点的深度值插值得到离群点的实际深度，从而达到修复点云的目的。首先根据已建立的三角网找出每个离群点的邻近点集，然后基于离群点的邻近点集进行局部二次曲面拟合，测站中心和当前离群点所连直线与二次曲面相交的点即为修正之后的离群点。

二次曲面方程的一般形式为：ax2+by2+cz2+dxy+exz+fyz+gx+hy+kz+1=0，方程所含未知参量较多[11-13]，只取与当前离群点有直接边连接关系的第一层闭环点有可能不足以完成曲面拟合，因此，本文在实验中选取每个离群点最近的两圈邻近点作为二次曲面拟合计算的样本点，采用文献[14]中提到的二次曲面拟合方法计算二次曲面方程。

如图6所示，修正离群点P是为了得到点P′(点P′代表相应物体表面缺失点)，点P′与点P的水平角α和竖直角θ相同，只是深度值ρ不同，而且点P′在拟合的二次曲面上。设点P′的极坐标为(α,θ,ρ)，其欧氏坐标表示如下：

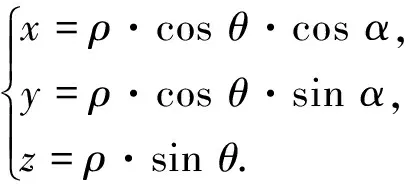
图6 离群点修正示意图

将上述坐标(只有ρ一个未知值)带入二次曲面方程求出点P′的坐标，遍历所有离群点完成点云修复。如图7(a)所示隧道内含有许多离群点，而且隧道表面出现了局部数据缺失，运用上述算法对该隧道点云处理后得到图7(b)，观察发现离群点被成功修正，隧道表面得到修复。

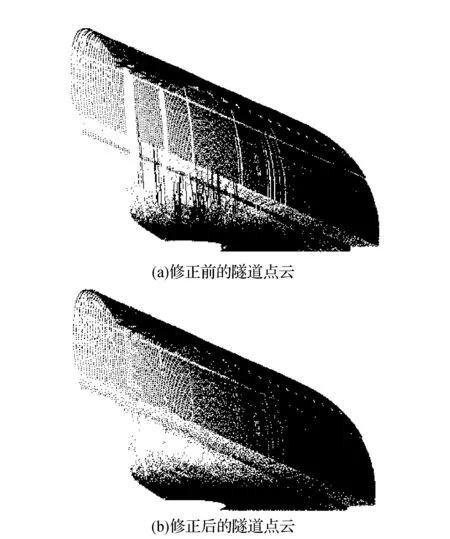
图7 修正前后隧道点云

4 实验结果与分析

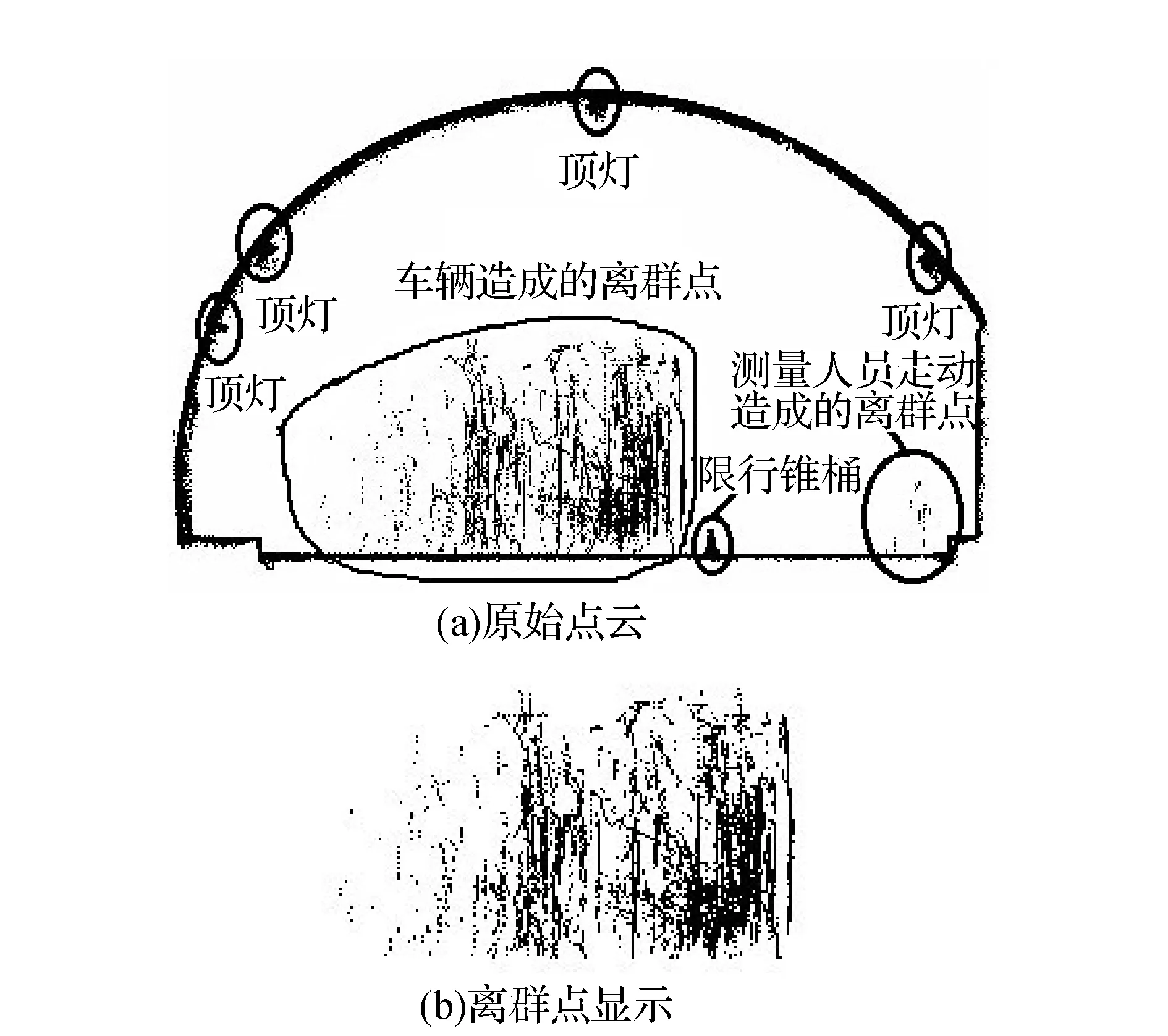
图8 完整隧道点云

利用VC++联合OpenGL编程实现了本文提出的离群点识别及修正算法并应用于宁杭高速公路梯子山隧道的一段实际扫描点云。如图8(a)所示为单测站隧道扫描点云(约42万个点)，包括：隧道内表面扫描点、拱顶吊灯扫描点、限行锥桶扫描点、以及通行车辆所致离群点和现场测量人员走动造成的离群点。应用本文提出的离群点识别算法处理后得到图8(b)。图8(b)所示车辆和行人造成的离群点都被识别出来且单独显示出来，而锥桶和隧道表面的顶灯并没有识别为离群点，表明该离群点识别算法能有效去除阶跃边缘点的影响。图9(a)和图9(b)所示为离群点修正之后的隧道点云，观察可以发现隧道点云得到了有效的修复。

图9 离群点修正后隧道表面

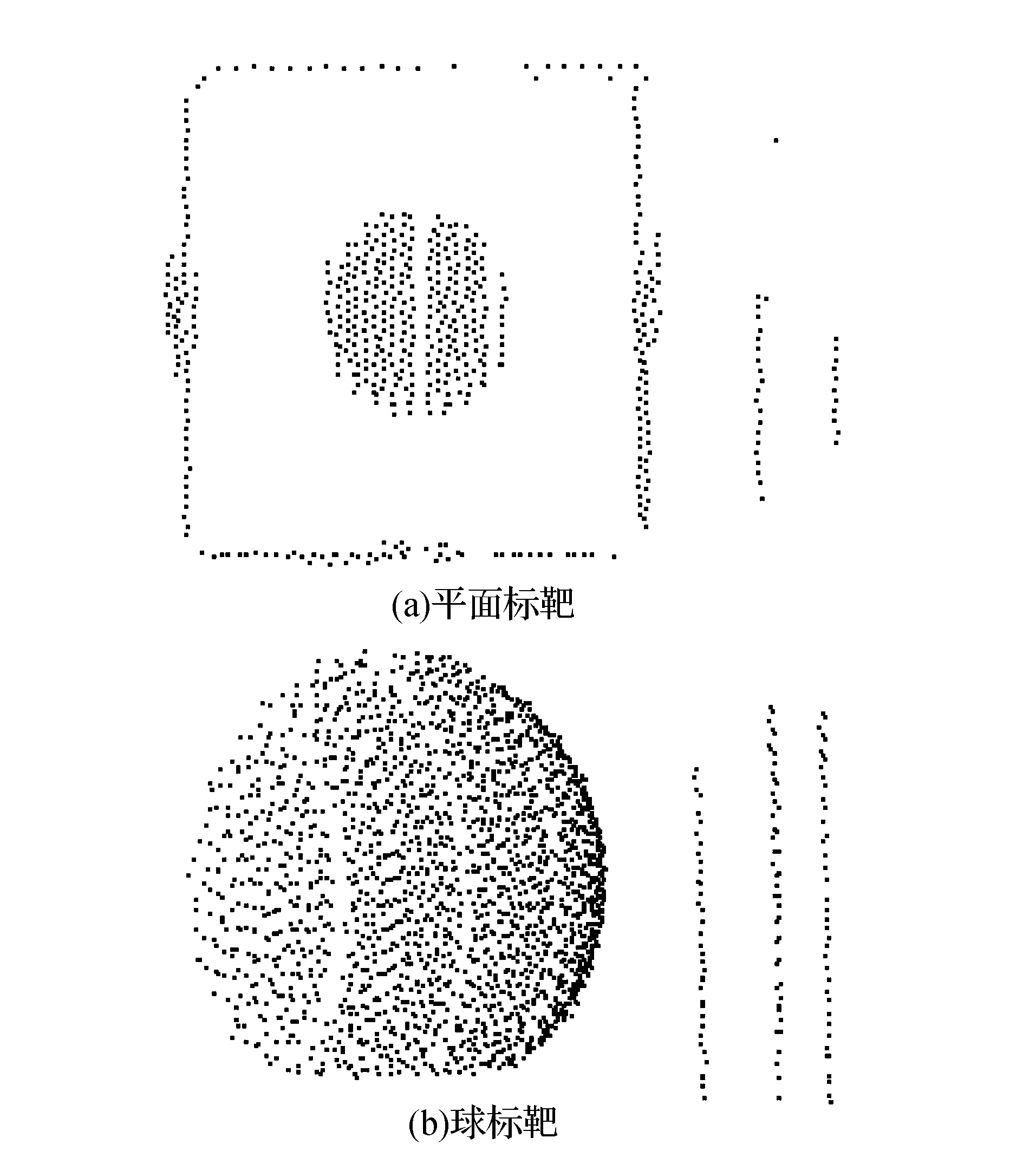
图10 平面标靶和球标靶点云

为了验证点云修复算法的准确性，本文专门设计了一组实验：对平面标靶和球标靶扫描过程中故意让行人通过造成离群点，所得点云如图10(a)和图10(b)所示，其中含有孤立和连续离群点。然后分别采用手工剔除离群点和本文提出的自动识别、修正方法，对处理后的标靶点云分别拟合中心坐标，并与实际中心坐标对比。如表1所示，拟合中心1和拟合中心2分别代表人工去除离群点后的拟合中心和点云修正之后的拟合中心，对比可发现人工去除离群点的平面标靶与球形标靶点云的拟合中心分别偏离实际坐标0.95 mm和0.16 mm，采用本文方法修复的平面标靶和球形标靶点云的拟合中心分别偏离实际坐标0.19 mm和0.07 mm。得益于本文提出方法对离群点的自动修复能力，有效保证了扫描点云的完整性，从而使建模精度显著高于将离群点视为粗差点简单剔除的处理方法。该实验也证明了本文提出离群点修复算法的准确性。

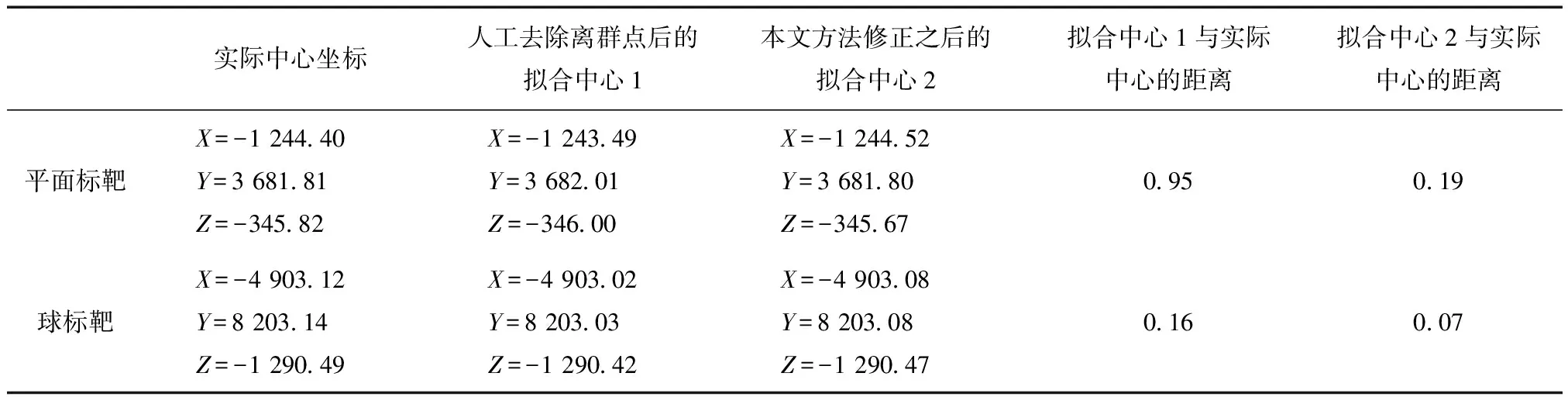
表1 点云拟合结果对比 mm

5 结束语

三维激光自动测量过程中由于瞬时遮挡造成的离群点属于偶然误差数据，三维激光扫描仪的等间隔均匀采样工作机制使得针对此类离群点的自动识别和自动修复成为可能。本文在分析此类离群点测量几何误差的基础上，设计了一种基于深度差的离群点识别方法，以及基于邻近点几何分布特性的离群点修正方法。利用隧道点云数据进行试验，试验结果表明该方法能够完成孤立离群点和连续离群点的自动识别和修复，能够有效排除阶跃边缘点对于离群点识别的影响，并且具有较高的修复准确性。该方法适用于原始测站扫描点云的初级去噪应用，不仅具有较高的处理效率，而且能够有效提高点云的完整性和后续建模的精度。

[1]LESLAR M，WANG J，HU B.Comprehensive Utilization of Temporal and Spatial Domain Outlier Detection Methods for Mobile Terrestrial LiDAR Data[J].Remote Sensing，2011，3(8)：1724-1742.

[2]赫春晓，李浩.基于三维激光扫描数据的三维实景构建[J].测绘工程，2013,22(1)：81-85.

[3]KNORR E M，NG R T，TUCAKOV V.Distance-based outliers：algorithms and applications[J].The VLDB Journal-The International Journal on Very Large Data Bases，2000，8(3-4)：237-253.

[4]BREUNIG M M，KRIEGEL H P，NG R T，et al.LOF：identifying density-based local outliers[C]//ACM Sigmod Record.ACM，2000，29(2)：93-104.

[5]高志国.海量点云数据滤波处理方法研究[J].测绘工程，2013,22(1)：35-38.

[6]张帆，黄先锋，李德仁.基于球面投影的单站地面激光扫描点云构网方法[J].测绘学报，2009，38(1)：48-54.

[7]郑德华，庞逸群，曹操.基于椭球面投影的散乱点云建立三角格网方法[J].测绘工程，2010，19(4)：19-23.

[8]孙正林，邹峥嵘，吴爱琴.一种改进的 Mean Shift 点云数据滤波[J].测绘工程，2011，20(5)：57-59.

[9]浮丹丹，周绍光，徐洋，等.基于主成分分析的点云平面拟合技术研究[J].测绘工程，2014，23(4)：20-33.

[10]江恒彪.基于实体化的地面点云建模技术[J].测绘工程，2014，23(7):30-33.

[11]席高文.二次曲面方程分类与化简的新方法[J].大学数学，2005，21(5)：129-134.

[12]于志路，姚吉利，马宁.真彩色点云三维模型方法研究[J].测绘与空间地理信息，2014，37(9)：119-121.

[13]张洪栋，刘翔，时振伟.影响地面三维激光扫描仪数据质量的因素分析[J].测绘与空间地理信息，2014，37(9)：183-186.

[14]郑德华.三维激光扫描数据处理的理论与方法 [D].上海：同济大学，2005.

[责任编辑：刘文霞]

Algorithm of recognizing and correcting the outlier based on depth difference

LI Jia,LIN Huan,LAN Qiu-ping,MA Fu-xun

(School of Earth Science and Engineering，Hohai University，Nanjing 210098，China)

The existence of outlier will bring interference to the following processing and application of the point cloud.For the outlier caused by the fast passing of car or pedestrian during the scans the algorithm of recognizing and correcting is proposed based on the depth difference.First，the mechanism is analyzed by the use of triangulation method based on the spherical projection to build the topology of the point cloud; then an algorithm using the depth difference to identify the outlier is proposed which can select corresponding threshold from different point cloud automatically; finally, a method is designed to repair the point cloud based on the quadratic surface fitting.Using the real tunnel data in the experiment，the results show that the algorithm has higher stability.

outlier;triangulation;ranging exception;quadratic surface fitting;interpolation

2013-09-26;补充更新日期：2014-10-20

国家自然科学基金资助项目(41201439)

李 嘉(1979-)，男，讲师.

P23

：A

：1006-7949(2014)11-0001-06