基于方向和距离关系的复合空间查询

王中辉，闫浩文，杨艳春

(1. 兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070； 2. 兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

基于方向和距离关系的复合空间查询

王中辉1，闫浩文1，杨艳春2

(1. 兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070； 2. 兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

利用四叉树索引，提出一种基于方向和距离关系的复合空间查询算法。其基本思路是：计算给定的方向区域和距离范围之间的交S,借助四叉树索引快速查找其MBR(Minimum Bounding Rectangle)被S包含或与S相交的空间对象，构成候选集，从候选集中删除不符合给定方向和距离关系的空间对象，得到查询结果。实验表明，算法具有较好的空间查询性能。

四叉树索引；方向关系；距离关系；复合空间查询；算法

空间查询是指从空间数据库中检索出满足给定空间关系的空间实体，它是GIS的核心功能之一，也是GIS区别于其它信息系统的本质特征，在航海、渔业、智能交通、环境监测等领域有着广泛的应用[1-2]。目前，空间查询的研究主要集中在方向或距离等单个空间关系上[3-6]。然而，在实际应用中，往往需要将方向和距离关系相结合，才能对空间目标进行准确查询。例如在查询图1中位于居民地A的北面，距离小于50 m的地块B1时，若基于方向关系查询，则结果为B1，B4两个地块；若基于距离关系查询，则结果为B1，B2，B33个地块。显然，在该情形下，只有将方向和距离关系相结合，地块B1才会被准确无误地查询出来。

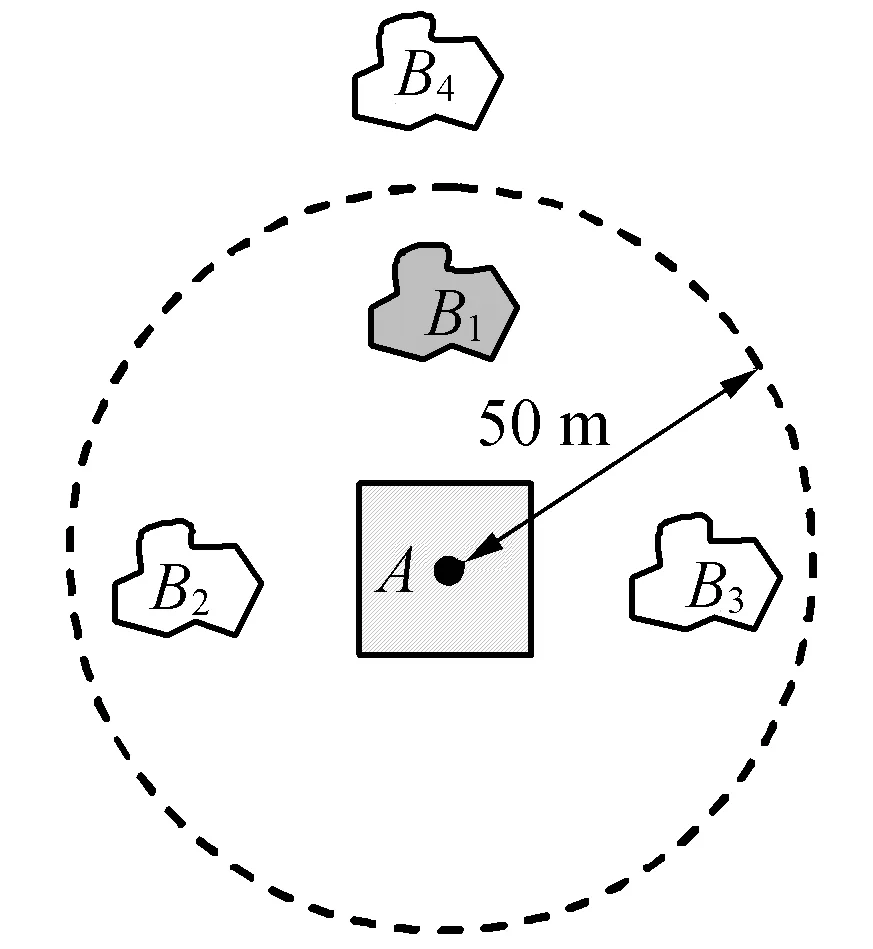
图1 结合方向和距离关系的空间查询

本文利用四叉树索引，提出一种基于方向和距离关系的复合空间查询算法。目的是能够在给定的方向和距离约束条件下，对点、线、面等空间对象进行有效检索，以提高空间查询的整体性能。

1 四叉树索引

空间索引是介于空间操作和空间对象之间的一种辅助性数据结构，通过它的筛选，大量与特定操作无关的空间对象被排除，使空间操作能够快速地访问操作对象，从而极大地提高空间查询的效率[7]。目前常用的空间索引主要有二叉树索引、格网索引、R树索引和四叉树索引等。

与其它空间索引相比，四叉树索引的优点是结构简单、数据冗余低，常用于加速空间对象间拓扑关系的计算。其基本思想是：将已知范围的空间划分成4个相等的子空间，如果需要可以将每个或其中几个子空间继续划分下去(树的深度由用户指定)，这样就形成了一个基于四叉树的空间划分[7]。其具体构建过程描述如下：

1)构建空四叉树。首先，计算空间对象的分布范围从而确定树的根节点矩形；然后，从根节点开始，将节点矩形平均划分为4个小矩形，创建出4个子节点，并对这4个子节点递归执行此过程，直至树的深度达到给定的值。此时所构建的四叉树是一个空的满四叉树。

2)插入空间对象。从根节点开始，如果当前节点包含空间对象的MBR，分两种情况插入该对象：①当前节点为叶节点：将空间对象插入到当前节点中；②当前节点为根节点或中间节点：判断当前节点的子节点是否包含空间对象的MBR，如果包含，则把该子节点作为当前节点，递归执行过程①、②；如果都不包含(相交或相离)，则将空间对象插入到当前节点中。

3)删除空节点。由上述过程创建的四叉树可能存在空节点，为节省存储空间，需要对它们进行删除。即从根节点开始，逐节点进行查找，如果当前节点没有子节点并且不含有空间对象，则删除该节点；如果当前节点包含子节点，则把子节点作为当前节点递归执行此过程，直至索引树中的所有节点都遍历完毕。

如图2所示，由于四叉树索引的根节点和中间节点都能够存储空间对象，且各节点所存储的空间对象不重复，因此它有效地降低了数据的冗余，具有较好的空间索引性能。为此，本文将选用四叉树作为空间查询的索引结构。

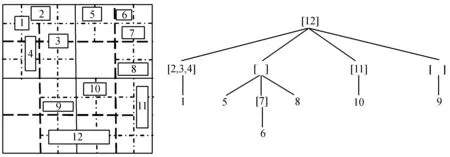
图2 四叉树索引

2 基于方向和距离关系的复合空间查询算法

2.1 方向关系计算模型

目前提出的方向关系计算模型主要有：矩形模型[8]、方向Voronoi图模型[9]、方向关系统计模型[10]、方向关系矩阵模型[11]和锥形模型[12]。

矩形模型的优点是简单、直观，但该模型对方向关系的描述太过近似，因此很少应用于空间查询；方向Voronoi图模型和方向关系统计模型对方向的描述虽然精确但计算复杂，不适合于高效率的空间查询；方向关系矩阵模型因受其方向区域划分方式的限制，只能进行八方向的空间查询，无法在实际中得到广泛应用。

锥形模型以参考对象的几何中心为起点，将空间划分为几个锥形方向区域，并通过判断目标对象与各方向区域之间的“交”是否为空，来描述空间方向。如图3所示，目标对象B与参考对象A的NE区域的“交”为非空，故B相对于A的空间方向关系为：Dir(A,B)=NE。与其它方向关系计算模型相比，锥形模型的优点是计算简单、实现容易，并且能够根据空间查询的不同需求，将空间划分为四方向、八方向、十六方向等锥形区域。为此，本文拟采用锥形模型作为空间查询的方向关系计算模型。

2.2 算法描述

图4中，A表示参考对象，锥形区域表示给定的方向区域，圆形区域表示给定的距离范围。本文算法的基本思路是：首先，计算给定的方向区域和距离范围之间的交，图4中的扇形区域OL1L2；然后，借助四叉树索引查找被OL1L2包含或与OL1L2相交的空间对象，得到查询结果，如图4中的阴影多边形。

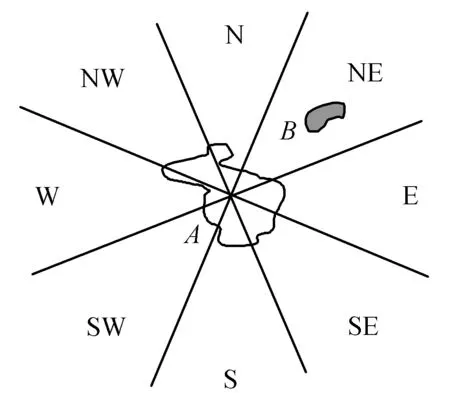
图3 锥形模型

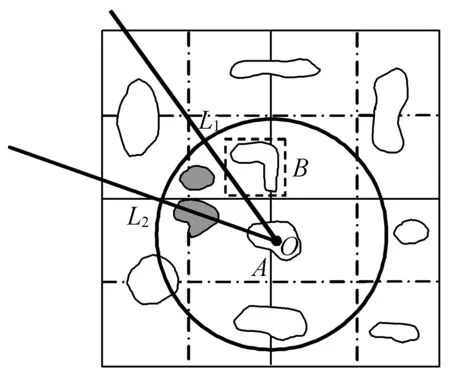
图4 基于方向和距离关系的复合空间查询

四叉树索引是用MBR近似表示空间对象，而MBR在许多情况下并不能正确代表空间对象自身与其它图形目标之间的拓扑关系。如图4所示，虽然空间对象B的MBR(虚线矩形)与扇形区域OL1L2相交，但B自身和OL1L2并不相交。为此，本文将空间查询分为以下两个过程：

1)过滤。利用四叉树索引快速查找其MBR被OL1L2包含或与OL1L2相交的空间对象，构成候选集。

2)提炼。从候选集中删除不符合给定方向和距离关系的空间对象，得到查询结果。

下面结合图4对算法的具体执行过程进行详细的描述。算法用到四叉树索引的一个重要特性，即四叉树索引的某个节点所表示的空间区域总是包含在其父节点所表示的空间区域中。

1)计算空间对象的MBR，建立四叉树索引。

2)计算给定的方向区域和距离范围之间的交OL1L2。

3)从四叉树的根节点开始，判断当前节点与扇形区域OL1L2之间的拓扑关系为：①当前节点与OL1L2相离，直接返回上一层；②当前节点包含在OL1L2内，将该节点(包括其子节点)存储的所有空间对象加入候选集，返回上一层；③当前节点与OL1L2相交，如果该节点存储了空间对象，判断每个空间对象的MBR与OL1L2的拓扑关系，如果相交或被OL1L2包含，则将该空间对象加入候选集；如果该节点还包含有子节点，则把子节点作为当前节点递归执行步骤3)，否则，返回上一层。

4)计算候选集中其MBR与OL1L2相交的空间对象和OL1L2之间的拓扑关系为：①空间对象与OL1L2相离，删除该对象；②空间对象被OL1L2包含或与OL1L2相交，保留该对象。

3 实验与讨论

本文利用C#语言编程实现了提出的复合空间查询算法，并使用不同几何类型的空间对象(点、线、面)进行实验。图5～图8是其中具有代表性的实验结果。图5、图6的查询对象为点，查询条件分别是“Direction = SE，10 d < Distance < 20 d”和“Direction = SW，Distance < 10d或Distance > 20 d”；图7的查询对象为线，查询条件是“Direction = NE，Distance < 20 d”；图8的查询对象为面，查询条件是“Direction = W，Distance > 10 d”。其中，符号d表示地图距离单位。

图5 实验1

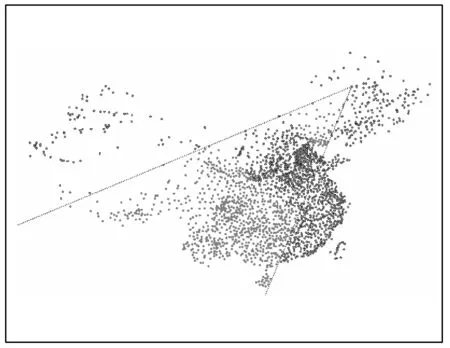
图6 实验2

图7 实验3

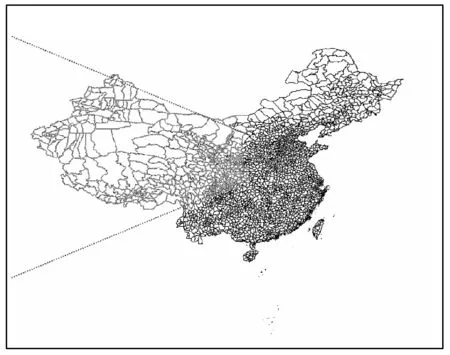
图8 实验4

为检验算法的查询性能，本文对利用四叉树索引(树的深度为4)和不利用四叉树索引的两种复合空间查询进行了对比测试。实验环境为Intel Core2 处理器(主频为2 GHz)，内存为2 GB，测试数据采用比例尺为1∶400万的矢量线目标数据(线目标的个数为11 333)。查询条件为“Directions = {N, NE, E, SE, S, SW, W, NW}，Distance < 20 d”。图9给出了两种方法的查询时间对比结果。

图9 查询时间对比

分析上述实验结果，可得出如下结论：

1)本文算法将方向和距离关系相结合进行空间查询，有效地提高了空间查询的准确性。

2)本文算法的通用性较好，能够处理不同几何类型的空间对象(点、线、面)。

3)本文算法采用四叉树作为空间索引结构，较好地提高了空间查询的效率。

4)本文算法的局限性在于：由于锥形模型将参考目标抽象为一个点，忽略了参考目标的形状和大小对方向关系的影响，当两目标之间的距离相对于自身大小较近时，容易出现查询上的偏差。如图10所示，在查询参考对象A以东(E)一定距离范围内的空间对象时，由于锥形模型自身的缺陷，使得空间对象B被漏查。

图10 算法存在的缺陷

4 结束语

本文利用四叉树索引，通过计算给定的方向区域和距离范围之间的交，实现了基于方向和距离关系的复合空间查询。实验表明该算法具有较好的空间查询性能。但由于锥形模型自身存在的缺陷，导致算法在某些情况下出现查询偏差。进一步的研究工作是对锥形模型进行改进，以完善复合空间查询的性能。

[1]陈晓斌, 葛文, 余慧明, 等. 基于网格的空间数据分布式查询技术研究[J]. 测绘工程, 2012,21(6):16-21.

[2]肖予钦, 张巨, 景宁, 等. 基于R树的方向关系查询处理[J]. 软件学报, 2004,15(1):103-111.

[3]夏宇,朱欣焰,苏科华.基于锥形模型的空间方向查询研究[J].地理空间信息,2007,5(3):65-67.

[4]付迎春, 袁修孝, 聂启祥. 扩展的锥形方向关系查询处理方法[J]. 计算机工程, 2008,34(15):36-38.

[5]张泽宝,张健沛,李若愚. R树的方向查询精过滤方法[J].哈尔滨工程大学学报,2010,31(11):1490-1495.

[6]李进,余建桥.空间对象的反最近邻查询处理技术研究[J].计算机工程与应用,2011,47(33):146-148.

[7]董鹏,李津平,白予琦,等.基于改进四叉树索引的矢量地图叠加分析算法[J].计算机辅助设计与图形学学报,2004,16(4):530-534.

[8]PAPADIAS D, EGENHOFER M. Algorithms for hierarchical reasoning[J]. GeoInformatica,1994,1(3): 251-273.

[9]YAN H, CHU Y, LI Z, et al. A quantitative description model for direction relations based on direction groups[J]. Geoinformatica, 2006, 10(2):177-196.

[10]DENG M, LI Z. A statistical model for directional relations between spatial objects[J]. Geoinformatica, 2008, 12(2):193-217.

[11]GOYAL R K. Similarity assessment for cardinal directions between extended spatial objects[D]. PHD Thesis, The University of Maine, 2000.

[12]PEUQUET D, ZHAN C X. An algorithm to determine the directional relation between arbitrarily-shaped polygons in the plane[J]. Pattern Recognition, 1987, 20(1): 65-74.

[责任编辑：刘文霞]

Compound spatial query based on direction and distance relations

WANG Zhong-hui1, YAN Hao-wen1, YANG Yan-chun2

(1. School of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

An algorithm for compound spatial query based on direction and distance relations is proposed by using quad-tree index. Its basic idea is: first, computing the intersection S of the given direction area and distance range; then, using quad-tree index to search quickly the objects whose MBR (Minimum Bounding Rectangle) contained by S or intersecting with S to construct the candidate set; finally, getting the result by removing the objects not meeting the given direction and distance relations in the candidate set. The experiments show that the algorithm has good performance.

quad-tree index; direction relations; distance relations; compound spatial query; algorithm

2013-09-09

国家科技支撑计划资助项目(2013BAB05B01)；数字制图与国土信息应用工程国家测绘地理信息局重点实验室开放研究基金资助项目(GCWD201210)；兰州交通大学青年科学基金资助项目(2013001)；地理空间信息工程国家测绘地理信息局重点实验室经费资助项目(201313)

王中辉(1978-)，男，讲师，博士研究生.

P208

：A

：1006-7949(2014)11-0007-04