天绘一号卫星三线阵影像RPC模型定位精度验证与分析

刘建辉，姜 挺，李延杰，李厚朴

(1.信息工程大学 地理空间信息学院，河南 郑州 450001; 2.65015部队，辽宁 大连 116023； 3.海军工程大学 导航工程系，湖北 武汉 430033)

天绘一号卫星三线阵影像RPC模型定位精度验证与分析

刘建辉1，姜 挺1，李延杰2，李厚朴3

(1.信息工程大学 地理空间信息学院，河南 郑州 450001; 2.65015部队，辽宁 大连 116023； 3.海军工程大学 导航工程系，湖北 武汉 430033)

天绘一号卫星以RPC参数作为主要的影像辅助数据提供给用户，对传感器的技术参数进行隐藏。文中简要介绍RPC模型的立体定位方法，并针对定位结果中存在的明显的系统误差，采用像方补偿方案进行补偿，最后利用两景天绘一号卫星三线阵影像RPC模型对测区进行实验验证和分析。结果表明，采用少量地面控制点进行系统误差补偿后，定位精度提升效果明显，验证了模型的正确性和有效性。

天绘一号卫星；立体定位；RPC模型；系统误差

天绘一号卫星[1]是我国首颗自主研制的传输型立体测绘卫星，卫星上搭载有三线阵立体测绘相机、高分辨相机和多光谱相机，可以获取全球范围内的立体、高分辨率和多光谱影像数据。立体测绘相机为三线阵推扫成像，分辨率为5 m，影像幅宽约为60 km×60 km。

鉴于对传感器成像参数的保密性，用户得到的天绘卫星影像产品主要为有理函数多项式模型，即RPC(Rational Polynomial Coefficients)模型，用户对卫星影像的几何处理或精度验证工作可以通过RPC模型的相关工作来完成。近十年来，国内外众多学者对RPC模型进行了深入的研究并得到了很多具有重要参考意义的结论。文献[2]详细介绍了RPC模型，包括建立模型、模型参数求解、参数优选以及RPC立体定位模型及区域网平差模型等。文献[3-4]利用IKONOS影像进行基于RPC模型的精确定位研究，表明系统误差补偿后定位精度能够得到明显提升。在此基础上，文献[5-7]在RPC模型中引入了误差补偿模型。文献[8]针对SPOT5 HRS影像进行了缺少地面控制点的区域网平差的研究，并利用SPOT5严密成像几何模型拟合RPC模型，在此基础上进行缺少控制点的SPOT5卫星影像平差处理。目前国内关于天绘卫星成像模型的精度验证工作进行的还比较少，其中，文献[9]介绍了天绘一号卫星无地面控制点条件下的摄影测量过程中的关键技术。文献[10]利用天绘一号卫星三线阵影像数据对登封嵩山遥感实验场进行RPC模型精度验证。文献[11-14]利用我国资源三号测绘卫星三线阵影像，构建了成像几何模型并对其几何精度进行了初步验证。

本文利用天绘一号卫星获取的两景河南某地区的三线阵影像，利用野外实测的一定数量的地面控制点对RPC模型的定位精度进行验证。实验证明天绘一号卫星三线阵影像具有较高的定位精度潜力。

1 RPC模型

RPC模型其实质是利用有理函数逼近二维像平面与三维物方空间的对应关系，从数学上去拟合影像的严格几何模型，因此单就RPC参数而言其并没有明确的物理意义，但其很好地实现了对传感器参数的隐藏，并具有良好的内插性能，RPC参数也逐渐成为广大影像供应商提供给用户影像数据的主要方式。

RPC模型的数学表达式可以定义为

(1)

pi(i=1,2,3,4)的表达式这里不再详细给出。为了避免物方和像方坐标因数量级差异过大而在计算过程中引起的舍入误差，需要将物方和像方坐标进行归一化，归一化需要的平移参数和尺度参数均可以根据提供的RPC参数文件中获取。物方和像方坐标归一化的公式可以表示为

(2)

其中：φ,λ,h分别表示物方点的纬度、经度和高程。Line,Sample为像元的行号和列号。***_OFF为平移参数，***_SCALE为尺度参数。

2 RPC模型的对地目标定位

2.1 立体定位模型

以单张影像为例，可以将RPC模型用 Taylor公式直接展开，得到误差方程式

(3)

为了获取高精度的定位结果，采用三视影像多片前方交会的方法进行物方点三维坐标的答解。由于每张影像的平移和尺度参数不一致，需要将归一化后的像方坐标(r,c)和物方坐标(P,L,H)统一重新表示为原始的像方坐标(R，C)和物方坐标(φ,λ,h)，可以得到误差方程表达式为

(4)

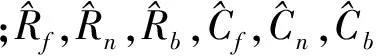
2.2 系统误差补偿模型

RPC参数由严格成像几何模型生成，因此严格成像几何模型的精度决定着RPC模型的几何精度。由于定轨测姿数据和影像数据获取时间的不同步，以及位置和姿态数据等存在的误差通常使直接定位的误差呈现明显的系统性，因此需要采用一定的数学模型对系统误差进行补偿[3-4]，通常在像方增加一个仿射变换

(5)

其中，ΔR和ΔC为像点坐标(R,C)的系统误差补偿值。在此基础上，RPC模型描述的像点和地面点之间的关系可以扩展为

(6)

该模型中均包含行方向上和列方向上的补偿参数，目的是分别吸收轨道和姿态测量误差在行方向和列方向上的影响。针对每一张影像，一个控制点可以列两个误差方程，上述形式含有6个未知参数(e0,e1,e2,f0,f1,f2)，因此至少需要3个地面控制点才能答解补偿参数。若只有少量地面控制点(少于3个)，则可以选择答解补偿参数(e0,f0)。

3 实验与分析

3.1 实验数据

实验所用数据是天绘一号卫星获取的两景河南某地区三线阵影像，将其编号为135影像和136影像，影像区域高差约900 m。其中，135影像采集控制点31个，136影像采集控制点10个。控制点均为野外GPS实测点，精度为分米级。控制点像点坐标为手工量测，精度在一个像素左右。实验所用的两景影像范围与控制点分布如图 1所示。

3.2 实验方案

1)由描述的RPC立体定位模型，对测区的两景三线阵卫星影像进行直接对地定位，观测其残差分布。

2)为了分析控制点的数量与分布情况对模型补偿后的定位精度的影响，设计了几种不同的实验方案[11]，具体方案描述如表1所示。

图1 影像范围与控制点分布

3)利用135影像的系统误差补偿参数，将其添加到136影像的RPC定位模型中，分析136影像的直接对地定位精度。

表1 实验分组方案

3.3 实验结果

表2为两景影像直接对地定位结果，图2、图3为对应的定位结果残差分布，表 3为135影像不同实验方案的实验结果。利用135影像RPC精化模型进行136影像的定位精度实验，实验结果如表4和图4所示。

表2 两景卫星影像无控制点RPC模型直接定位结果

图2 135影像直接定位残差分布

图3 136影像直接定位残差分布

表3 135影像不同方案实验结果

表4 误差补偿后135影像定位结果及136影像定位结果

注：135影像定位结果为采用5个控制点(四周+中心)进行系统误差补偿方案;136影像定位结果为引入135影像解算的仿射系数进行立体定位得到。

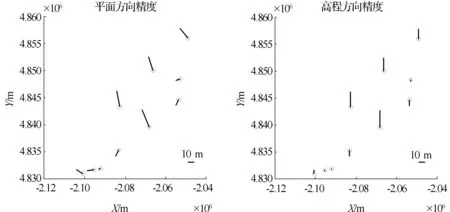
图4 采用135影像解算的补偿参数进行136影像定位结果的残差分布

3.4 实验分析

1)分析表 2、图 2、图 3可知，两景三线阵卫星影像直接定位结果差异不大，平面方向精度约为30 m，高程方向精度约为10 m。由残差分布可知定位结果中含有比较明显的系统误差，有必要对其进行消除，以免影响后续的几何处理。

2)分析表3可得，仅采用一个控制点进行系统误差补偿便可以使定位精度大幅度提升，采用更多的控制点参与模型精化其定位精度会进一步提升但效果有限，这说明天绘一号卫星影像在行方向和列方向存在的误差主要为沿各方向的平移误差。

3)利用135影像的系统补偿参数作用于136影像，136影像的定位精度提升明显，其中平面精度提升63.16%=(29.10-10.72)/29.10；高程精度提升70.37%=(10.53-3.12)/10.53。说明在此成像间隔内，卫星运行状态平稳，两景影像中残留的系统误差基本一致。根据这一结论，可以得出在控制点难以获取的地区，如高原，山地地区等，可以采用此方法对该地区进行相关的定位或测图等工作。鉴于实验数据所限，实际情况还有待进一步验证。

4 结 论

本文对天绘一号卫星的RPC模型的几何定位精度进行了相关的实验验证。可以得出，天绘一号卫星RPC模型的直接对地目标定位精度可以达到平面精度30 m左右，高程精度10 m左右，采用少量地面控制点进行模型精化后，定位精度提升明显，并且其RPC模型可以用于影像覆盖区域的外推定位中，说明天绘一号卫星具有较高的定位精度潜力。此外，由于选择控制点的方案不同以及其他因素，改进模型的定位结果可能会有细微差异。

[1]杨俊峰,张献瑞.天绘一号卫星数据产品及应用[C]. 第一届全国高分辨率遥感数据处理与应用.美国:美国科研出版社,2011.

[2]张永生,巩丹超,刘军.高分辨率遥感卫星应用—成像模型、处理算法及应用技术[M].北京:科学出版社,2004.

[3]刘军,张永生,王冬红.基于RPC模型的高分辨率卫星影像精确定位[J].测绘学报，2006,35(1):30-35.

[4]刘军,王冬红,刘敬贤，等.利用RPC模型进行IKONOS影像的精确定位[J].测绘科学技术学报，2006, 23(3):228-232.

[5]C V Tao, Y Hu, J B Mercer. Image Rectification Using A Generic Sensor Model-Rational Function Model[C]. Amsterdam: 2000.

[6]C S Fraser, H B Hanley. Bias-Compensated RPCs for Sensor Orientation of High-Resolution Satellite Imagery [J]. Photogrammetric Engineering&Remote Sensing, 2005, 71(8): 909-915.

[7]H B Hanley, C S Fraser. Sensor orientation for high resolution satellite imagery: further insights into bias compensated RPCs[M]. International Archives of Photogrammetry and Remote Sensing, Denver,USA,2002,35(Part B1):24-29.

[8]李德仁,张过,江万寿,等. 缺少控制点的SPOT-5 HRS影像RPC模型区域网平差[J]. 武汉大学学报：信息科学版，2006,31(5): 377-381.

[9]王任享,胡莘.天绘一号无地面控制点摄影测量[C].第十八届中国遥感大会.北京:科学出版社,2012.

[10]刘军,张永生.天绘一号影像RPC模型嵩山实验场精度验证[C].第一届高分辨率遥感数据处理与应用.美国:美国科研出版社，2011.

[11]唐新明,张过,祝小勇,等.资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J].测绘学报，2012，41(2):191-198.

[12]李霞，朱倩，邓良.几种天绘一号卫星影像分割方法及质量评价[J].测绘科学，2014，39(9)：60-64.

[13]徐巍，陈帅.机载激光雷达系统定位精度分析[J].测绘与空间地理信息，2014，37(7)：137-140.

[14]张爽，秦杨，朱晓文.浅谈地理国情卫星影像的质量控制[J].测绘与空间地理信息，2014，37(6)：215-217.

[责任编辑：刘文霞]

Verification and analysis of positioning accuracy of RPC model of TH-1 three-line imagery

LIU Jian-hui1, JIANG Ting1, LI Yan-jie2

(1.Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China; 2.Troops 65015, Dalian 116023, China; 3.Department of Navigation, Naval University of Engineering, Wuhan 430033, China)

TH-1 satellite’s administer sends RPC to the users as the main auxiliary data in order to hide the sensor’s technique parameters. The methods of stereo positioning based on the RPC model, and the key problem of obvious systematic error is analyzed, and then through adding an affine transformation in image space the systematic error is compensated. Experiment is made through two TH-1 satellite three-line images based on RPC model. The test result shows that few ground control points can improve the positioning precision of bias compensated RPC model greatly, and demonstrates the correctness and effectiveness of RPC model.

TH-1 Satellite; stereo positioning; RPC model; systematic error

2013-10-13；补充更新日期：2014-10-15

国家自然科学基金资助项目(41471387)

刘建辉(1986-)，男，博士研究生.

P228

：A

：1006-7949(2014)11-0025-05