任意坐标系下的多块规则格网DEM拼接

杨韫澜，胡海彦，高 力

(1.长安大学,陕西 西安 710054;2.61363部队，陕西 西安 710054;3.信息工程大学 地理空间信息学院,河南 郑州 450052;4.地理信息工程国家重点实验室,陕西 西安 710054;5.西安测绘研究所,陕西 西安 710054)

任意坐标系下的多块规则格网DEM拼接

杨韫澜1，2，胡海彦3，4，5，高 力3，4，5

(1.长安大学,陕西 西安 710054;2.61363部队，陕西 西安 710054;3.信息工程大学 地理空间信息学院,河南 郑州 450052;4.地理信息工程国家重点实验室,陕西 西安 710054;5.西安测绘研究所,陕西 西安 710054)

将高精度影像匹配技术用于具有重叠区域的规则格网DEM同名高程点提取，提出任意坐标系下的多块规则格网DEM高精度无缝拼接方法。方法的特点是可以在任意坐标系下(自由坐标系、绝对坐标系)对存在重叠区域的任意大小、任意数量和任意区域形状的规则格网DEM模块进行拼接，整体性地求解拼接参数，得到无几何错位的高精度DEM。通过实验，证明拼接方法的有效性和实用性。

数字高程模型；规则格网；拼接；影像匹配；区域网平差

数字高程模型的具体形式和数学表述多种多样，诸如等高线(Contours)、不规则三角格网(TIN)、规则格网(GRID)甚或空间特征点/线混合体数据集等都是GIS应用分析中常用的DEM形式。这些具体形式各有优缺点，其中规则格网DEM因结构简单且便于数据压缩、存储而被普遍采用[1]。

无论是在规则格网DEM的生产过程中，还是在已有DEM产品的后期应用中，都需要将多块DEM进行拼接，生成更大区域范围的DEM。如果是在绝对坐标系下，将已有多块规则DEM产品进行拼接，假设各个DEM模块精度满足产品规范，则最直接的拼接方式是根据绝对位置，直接将这些DEM块进行拼接，重叠区域的高程进行加权平均处理即可。这种方法虽然拼接后DEM精度满足要求，但会在重叠区域产生“陡坎”和错缝[2]。针对此问题的改进拼接方法[3]仍存在适用面较窄，只能在统一或绝对坐标系下进行拼接处理等缺陷。

如果是在自由坐标系下，典型案例如摄影测量中的相对定向，往往是在单个立体像对的基线坐标系下进行，现有方法[4-6]必须经过立体像对模型连接、航线连接及区域网平差后，再进行前方交会，生成各立体像对绝对坐标系下DEM，最后再进行DEM拼接，处理过程冗长，易产生误差积累。如果相对定向完成后，利用密集影像匹配技术配合前方交会即可得到该自由坐标系下的DEM模块，进而利用本文的拼接方法则可以直接将这些“自由”的DEM模块进行拼接，从而快速得到更大区域范围的DEM模型。

本文提出的任意坐标系下的多块规则格网DEM拼接方法，可以在任意坐标系下(自由坐标系、绝对坐标系)对存在重叠区域的任意大小、任意数量和任意区域形状的规则格网DEM块进行拼接，整体性的求解拼接参数，可以取得严丝合缝，无几何错位的高精度DEM拼接效果。

1 多块DEM格网拼接

以6块大小不一的矩形区域DEM格网块为例，平面投影见图1(理论上，各个DEM块可为任意形状，只要相邻DEM模块存在一定重叠区域即可)，用于DEM格网拼接的高程连接点有两类：第一类是位于重叠区域的同名高程点1～15，其用于确定DEM格网块之间的相对拼接关系；第二类是位于某个/些DEM格网块上的基准控制点A～E，其作用是用来确定拼接后DEM格网块在控制坐标系中的绝对位置关系。本文只用6个DEM格网块进行示意，更多块DEM格网拼接所需的连接点与之类似。整个DEM格网拼接流程分为3个步骤：1)同名高程连接点提取；2)拼接模型建立及拼接参数区域平差计算；3)利用计算所得拼接参数进行DEM拼接(包括模型变换与格网点高程值重采样)。

1.1 同名高程连接点提取

如将规则格网DEM每个点的高程值类比为数字影像每个像素的灰度值，则可将DEM模块视为影像矩阵数据块，这样可以利用角点探测和同名点影像匹配技术提取同名高程点。最直接的方式就是将DEM数据以raw影像数据格式进行运算和操作。图2为任意两块具有重叠区DEM格网的“影像化”及同名点匹配过程示意。计算机视觉软件库OpenCv/EmguCv[7]中实现多种角点特征的提取方法，包括：Harris角点、ShiTomasi角点、亚像素级角点、SURF角点、SIFT角点、Star关键点、FAST关键点、Lepetit关键点等等，并且实现与角点探测密切相关的Sobel算子、拉普拉斯算子、Canny算子、霍夫变换等多种图像变换算法[7]。考虑DEM拼接精度及影像匹配的时间效率，选择亚像素级角点探测方法用于“DEM影像”的同名高程点提取。

图1 大小不一的6块矩形区域DEM格网及假定的同名高程点和基准控制点分布

图2 任意两块有重叠区DEM格网的“影像”化及同名高程连接点匹配

1.2 拼接模型建立及拼接参数平差计算

获取相当数量的同名高程连接点后，就可以利用这些同名高程点将这些模型“缝制”起来。以目标参考位置为基准，这些“自由”的DEM模型在三维空间上产生平移、旋转和缩放变换，所以可选择三维等形变换作为DEM的数学拼接模型，矩阵式见式(1)。

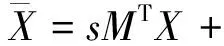
(1)

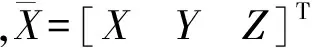
根据高程点种类及式(1)，可以给出两类拼接关系方程。

1.2.1 基于基准控制点的拼接关系方程

以图1中V号DEM模型上的基准控制点C为例，根据式(1)，有

(2)

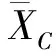
1.2.2 基于相邻DEM模型同名高程点的拼接关系方程

利用相邻DEM模型上的同名高程点所对应的拼接后DEM模型点绝对坐标相等这一条件列出拼接关系方程，以图1中相邻DEM模块I和模块II上的同名点1为例，有

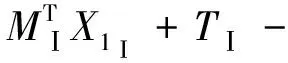
(3)

式中:X1Ⅰ,X1Ⅱ是1号同名高程点在DEM模型Ⅰ、Ⅱ上的模型坐标;sⅠ,MⅠ,TⅠ和sⅡ,MⅡ,TⅡ分别对应Ⅰ、Ⅱ号DEM模型的7个拼接参数。图1中各个同名高程点及与之对应的相邻DEM模型拼接关系见表1，依据表1可对其它每对相邻DEM模型及相应重叠区中出现的每个同名高程点按式(3)列出一组拼接关系方程组。

由于式(1)为非线性系统，需要线性化进行牛顿迭代最小二乘求解，关于三维等形变换的具体线性化过程和系数的具体形式可参考文献[8]。这样，将所有基准控制点及同名高程点所列出的拼接关系观测方程组进行组合，得到的观测方程组矩阵式为

mAnnX1=mL1+mV1.

(4)

式中：系数矩阵A按照两种拼接关系组建;X为所有DEM模块的拼接参数;L为由元素0和基准控制点绝对坐标与其对应式(1)的泰勒展开式0阶常数项的差值组成;V为残差向量;m大小与同名高程点数量、重叠度及基准控制点数量有关，对于图1，参考表1，有m=(25+5)×3=90；n大小为DEM块数量的7倍，对应有n=6×7=42。拼接参数可通过最小二乘平差解求，X=(ATA)-1(ATL)，这些参数即确定所有DEM模型到拼接后DEM模型的几何拼接关系。对于拼接精度，可按式(5)进行计算。

V=AX-L.

(5)

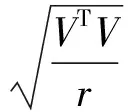
表1 各个同名高程点及与之对应的相邻DEM模型连接关系

1.3 DEM拼接

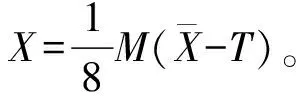
对于拼接后DEM(图1(b)中的外接矩形)中的某一格网点，其必然落在以下3类区域之一：第一种格网点位于“无效区”，即使用对应DEM模型拼接参数计算所得模型坐标位置不会落在相应DEM模块的有效模型坐标范围内，即是无效的，这时拼接后DEM在此处的高程值可用指定代表无效值的数值填充；第二种网格点位于非重叠区，其高程值只能直接使用所在DEM模块对应位置处的采样高程值进行填充；第三种网格点位于相邻DEM块重叠区域内，此时，可在包含重叠区的任意一个或多个DEM块上采样得到高程值，然后进行高程值的加权平均即可。这样，逐个格网点依据3种情况中的对应一种进行格网点处高程值的采样和填充，直至最终拼接DEM的生成。

2 实验及分析

2.1 试验数据

利用数字航摄影像进行规则格网DEM测绘产品制作试验，所用相机焦距为171 mm，像幅14 K×12 K，像元大小9μ。航摄区域为汉中某山地与平地接壤区，最大高差300 m，摄影高度3500 m，GSD为20 cm，东西方向3条航线。研究区域约5 km×5 km，覆盖21个立体像对。为验证DEM精度，在该范围进行密集布控，点数为324个，XYZ3个方向精度优于1 cm。

2.2 试验流程及效果分析

为了验证本文提出的任意坐标系下的多块规则格网DEM拼接方法，先对测区内21个立体像对分别进行相对定向，形成21个自由坐标系下的立体像对模型；其次，密集匹配同名像点后进行前方交会，得到对应的三维点云数据，内插得到自由坐标系下的21个规则格网DEM；最后，利用测区四角和中央共计5个控制点以及这21个具有一定重叠度的DEM模块，按前面介绍的拼接方法进行拼接，得到大范围的规则网格DEM产品，利用该DEM产品可内插生成等值线图或三维透视图(如图4、图5所示)。

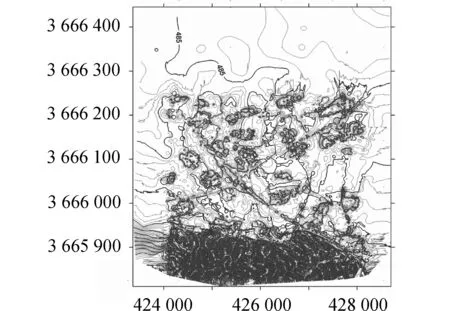
图4 21个DEM模块拼接后等高线绘制

图5 影像叠加透视图

具体拼接过程中，在21个DEM模块的32条重叠区域条带里，共提取同名高程点2847个，加上5个控制点，利用这些点位空间信息解算了21套共计21×7=147个拼接参数。为了检查拼接后DEM有无拼接痕迹，图4中特别采用0.5 m等高距进行等高线绘制，无论是等高线绘图显示，还是透视图(图5)都看不到陡坎和几何错位、错缝等现象，可谓严丝合缝。进一步利用同名高程点进行拼接精度统计，XYZ方向综合拼接精度为σ0=0.43，不到1/4格网间距和等高距。为了更进一步检查拼接后DEM的整体绝对精度，将319个外业控制点作为检查点进行精度统计，最大高差0.85 m，高差平均值0.02 m，标准差0.01 m，完全满足DEM产品规范精度要求。

3 结 论

利用影像匹配技术和区域网平差技术，提出任意坐标系下多块规则格网DEM高精度无缝拼接方法。该方法的特点是在DEM拼接过程中，进行所有拼接参数的一次性整体求解，从而保证DEM的无缝高精度拼接效果，处理过程简短且灵活，易于实现高度自动化，减少拼接工作量和繁琐的人工干预。

[1]李志林，朱庆.数字高程模型[M].武汉：武汉大学出版社，2001.

[2]苏媛媛.DEM的自由拼接及其栅格转换技术[J].军民两用技术与产品，2007(6):47-48.

[3]杨国平，王明孝. DEM的自由拼接及可视化检查[J].测绘学院学报，2003，20(4):279-281.

[4]金为铣，杨先宏，王树根. 独立模型法区域网平差的一种新的计算方法[J]. 武汉测绘学院学报，1985(3) :77-86.

[5]周小军，王光霞，薛志伟，等. 基于DEM化简的等高线综合研究[J]. 测绘工程，2014，23(2): 10-14.

[6]赵培洲，张世远. 采用独立模型法和航带法区域网平差的试验成果[J]. 测绘学报，1987，16(1): 51-56.

[7]BRADSKI G. The opencv library[J]. Doctor Dobbs Journal, 2000，25(11): 120-126.

[8]Wolf P R，DEWITT B A. Elements of Photogrammetry: with applications in GIS[M]. New York: McGraw-Hill，2000.

[责任编辑：张德福]

Stitching DEM Grids in arbitrary coordinates

YANG Yun-lan1，2,HU Hai-yan3，4，5，GAO Li3，4，5

(1．Chang’an University，Xi’an 710054，China； 2．Troops 61363，Xi’an 710054，China；3．School of Geospatial Information，Information Engineering University，Zhengzhou 450052，China；4．State Key Laboratory of Geo-information Engineer，Xi’an 710054，China；5．Xi’an Institute of Surveying and Mapping，Xi’an 710054，China)

Based on exacting of corresponding points in overlap of neighboring DEM grids using image matching in high accuracy, an approach of stitching numberless DEM grids seamlessly in arbitrary coordinates is presented which is not astricted by the shape and range of grids. The characteristic of the method is that the stitching parameters can be solved simultaneously so the resultant DEM is glossy in the juncture and without malposition. Experiment data set with aerial image stereo pairs is tested by the presented approach here and the result is analyzed.

DEM; Grid; stitching; image matching; block adjustment

2014-06-10

杨韫澜(1978-)，女，工程师，博士研究生.

P208

：A

：1006-7949(2014)11-0030-04