基于遗传算法的PID 整定

陈正岸

(广东粤电湛江生物质发电有限公司，广东湛江524000)

1 遗传算法简介

1.1 遗传算法的定义及原理

遗传算法是从代表问题可能潜在解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体，它决定了个体的形状外部表现。因此，需要实现从表现型到基因型的映射编码工作。由于仿照基因编码的工作很复杂，需要进行简化，如二进制编码。初代种群产生之后，按照优胜劣汰的原理，逐代演化产生出越来越好的近似解。在每一代，根据问题式中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出新的解集种群。末代种群中的最优个体经过解码，可以作为问题近似最优解。

遗传算法模仿生物遗传及进化的步骤，以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合，在问题空间进行全局并行的、随机的搜索优化，求得问题的全局最优解。遗传算法模仿生物遗传及进化的步骤，引人了如繁殖、交叉、变异等方法。

1.2 遗传算法的应用

由于遗传算法的整体搜索策略和优化搜索方法在计算时不依赖于梯度信息或其他辅助知识，只需要影响搜索方向的目标函数和相应的适应度函数，所以遗传算法提供了一种求解复杂系统问题的通用框架，它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，所以广泛应用于许多科学。例如，函数优化、权值优化、组合优化、结构优化。

2 基于遗传算法的PID 参数寻优设计

2.1 参数的确定及表示

PID 控制器中一般微分时间为0，所以选取比例带δ 和积分时间Ti 为参数，我们的任务是离线寻找最合适的参数，以使控制器的控制达到最优。首先确定参数范围，该范围一般由用户给定，根据经验设 δ∈［0，5］，Ti∈［0，100］，然后由精度的要求，对其进行编码。选取10 位的二进制字串来表示每一个参数，并建立与参数的关系，再把两个参数的二进制连接起来组成一个长的二进制字串，该字串为遗传算法可以操作的对象。

2.2 选取初始种群

因为需要编程来实现各过程，所以采用计算机随机产生初始种群即先产生0 ～1 之间均匀分布的随机数，然后规定产生的随机数 0 ～0.5 之间代表 0，0.5 ～1 之间代表 1。此外，考虑到计算的复杂程度，规定种群的大小为迭代，也就是迭代20 次。

2.3 适配函数的确定

一般的寻优方法在约束条件下可以求得满足条件的一组参数，在设计中是从该组参数中寻找一个最好的。衡量一个控制系统的指标有三个方面，即稳定性，准确性和快速性。而上升时间反映了系统的快速性，上升时间越短，控制进行就越快，系统品质也就越好。

实际应用中系统中固有的饱和特性导致系统不稳定，为了防止控制能量过大，在目标函数中加入控制量。因此，为了使控制效果更好，我们给出了控制量，误差和上升时间作为约束条件。适应函数同目标函数相关，目标函数确定后，直接将其作为适配函数进行参数寻优。最优的控制参数就是在满足约束条件下是f(x)最大时，x 所对应的控制器参数。

2.4 遗传算法的操作

利用遗传算法优化Kp，Ki，Kd 的具体步骤如下。

1)确定每个参数的大致范围和编码长度，进行编码。

2)随机产生n 个个体构成初始种群P(0)。

3)将种群中各个体解码成对应的参数值，用此参数求代价函数值J 及适应函数值f，取f=1/J。

4)应用复制，交叉和变异算子对种群P(t)进行操作，产生下一代种群P(t+1)。

5)重复步骤3)和4)，直至参数收敛或达到预定的指标。

3 遗传算法应用举例

3.1 实例分析

通过计算机编程实现以上功能，选取单回路寻优控制回路实例做进一步分析。实例:某单回路寻优控制回路如图1 所示，其中被控对象为二阶传递函数:

G(s)=300/(s2+30s)，PID 为 U(S)= Kp(1 +1/TiS +TdS)。采样时间为1 ms，输入为阶跃信号。

图1 控制系统图

为获取满意的过渡过程动态特性，采用误差绝对值时间积分性能指标作为参数选择的最小目标函数。为了避免超调，采用超调量作为最优指标的一项，此时的最优指标为:

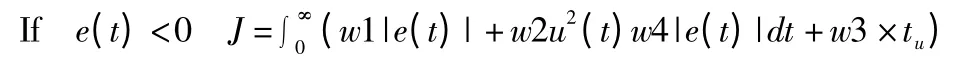
e(t)为系统误差，u(t)为控制器输出，tu为上升时间，w1，w2，w3，w4 为权值。

采用二进制编码方式，用长度为10 位的二进制编码串来分别表示三个决策变量Kp，KI，Kd。最优指标的选取同十进制编码遗传算法的PID 整定。遗传算法中使用的样本个数为Size =30，交叉概率和变异概率分别为:pc=0.06，pm=0.01 －［1 ∶1:Size］。参数 Kp的取值范围为［0，20］，KI，Kd的取值范围为［0，1］，w1，w2，w3，w4 的取值同十进制编码遗传算法的PID 整定。经过100 代进化，最优个体为 BestS=［010000011101011100100000100110］。

PID 优化参数为:Kp =17.556 2，Ki =0.391 0，Kd =0.306 9，性能指标 J=27.364 3。

3.2 遗传算法和衰减曲线法的simulink 仿真性能比较

为显示用遗传算法进行参数优化的优越性，用遗传算法和工程上常用的衰减曲线法进行了PID 参数整定与优化，并进行效果性能的比较。我们用MATLAB 的Simulink 搭建的模块图去模拟实际的工程，Simulink 接线如图2，输入信号都为单位阶跃信号。

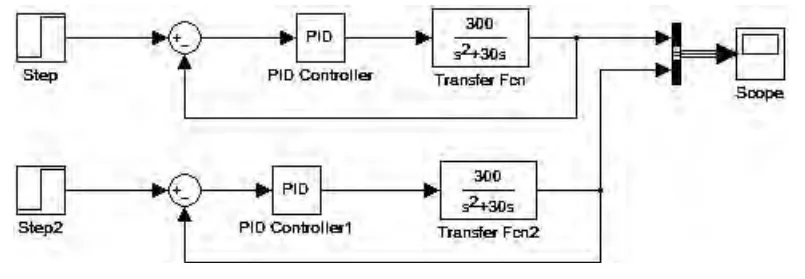
图2 仿真结构图

用两种方法整定出PID 的参数，在两个PID 控制中填入相应的参数值，最后运行可以得出两条输出响应曲线如图3。

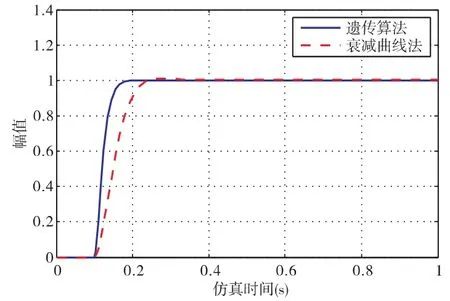
图3 阶跃响应曲线

通过上图的仿真实验表明，从两条阶跃响应曲线可以看出，遗传算法的调节时间比衰减曲线法的调节时间短，超调量比衰减曲线法小。遗传算法优化出来的PID 参数在应用到实际中得出的系统响应动态效果明显，比衰减曲线法的参数好。

3.3 鲁棒性分析

被控对象在运行过程中可能出现劣性变化时，对象的时间常数T 增大，静态增益K 减小，此时，控制系统的控制水平会发生的变化是工程上必须考虑的重要问题。当时间常数T 增加50%后，原来被控对象变G'(s)=10/(0.05s2+s)，定值扰动信号为单位阶跃信号来检验系统的鲁棒性。PID 采用遗传算法优化参数 Kp=17.556 2，Ki =0.391 0，Kd =0.306 9，用衰减曲线法整定出来的 PID 的参数为 Kp =3.062 5，Ki =0.180，Kd =0.060，两种方法鲁棒性比较如图4

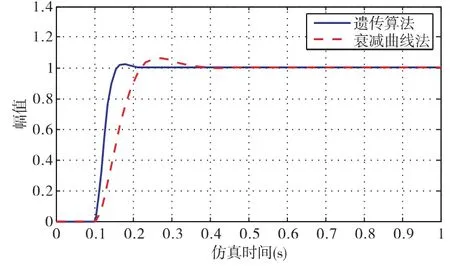
图4 响应曲线

从上图曲线中可以看出，鲁棒性测试中，对象发生了结构和参数的变化，基于遗传算法PID 参数优化方法下的控制效果仍比较好，可以说该方法具有较强的鲁棒性。

4 结语

遗传算法运用于PID 的参数整定，不但克服了常规PID 整定方法的缺点，而且还避免了基于专家系统的PID 参数整定方式中知识库建立的困难性，实现PID 参数离线整定。如果把该方法运用于工业控制过程的上位机，结合系统辨识可以实现PID 在线参数整定。

［1］周明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999.

［2］金以慧，方宗智.过程控制［M］. 北京:清华大学出版社，2008.

［3］薛定宇.控制系统仿真与计算机辅助设计［M］. 北京:机械工业出版社，2005.

［4］黄忠霖.控制系统 MATLAB 计算及仿真［M］.北京:国防工业出版社，2009.

［5］刘金昆.先进 PID 控制及其 MATLAB 仿真［M］.北京:电子工业出版社，2003.

［6］刘娜，韩璞，甄成刚.基于遗传算法的PID 参数寻优［J］.计算机仿真，2002，19(2):.

［7］毛敏，于希宁. 基于遗传算法的 PID 参数优化方法［J］.中国电力.2002，35(8):48 －51.

［8］陈祥光.遗传算法在PID 控制器参数寻优中的应用研究［J］.计算机真，2001，18(2):.

［9］刘俊丽，韩旭. 遗传算法技术浅论［J］. 电脑学习，2009，5:142 －143.

［10］丁寅磊，吕丽霞.基于遗传算法的PID 控制器参数优化研究［J］.仪器仪表用户，2009(1).