一类向量优化问题的弱有效解的Kuhn-Tucker充分条件

蒋娅

(西华师范大学数学与信息学院，四川南充637002)

一类向量优化问题的弱有效解的Kuhn-Tucker充分条件

蒋娅

(西华师范大学数学与信息学院，四川南充637002)

在Banach空间中，利用几类广义不变凸的概念，获得了一类向量优化问题的弱有效解的Kuhn-Tucker型充分条件，改进和推广了已有文献中的一些相应结果．

弱有效解；最优性充分条件；广义ρ-不变凸；广义ρ-伪不变凸；广义ρ-拟不变凸

最优化理论包含许多重要的内容，其中对于向量优化问题的各种解的最优性条件的研究是许多学者感兴趣的课题．1999年李泽民[1]在线性拓扑空间中讨论了集值问题的弱有效解的最优性条件，并在实线性空间中讨论了集值问题的弱有效解的最优性条件[2]；他以Frechet导数为工具，导出了向量集值问题的K-T型一阶充要条件以及二阶充分条件，讨论了半无穷向量最优化问题的最优性条件[3]，推广了陈光亚[4]的结果．本文在Banach空间中，利用几类广义不变凸的概念，讨论了一类向量优化问题的弱有效解，获得了弱有效解的Kuhn-Tucker型充分条件，改进和推广了已有文献中的一些相应结果．

1 基本概念及引理

设X是Banach空间,Y是局部凸的Hausdorff空间,具有内部非空的正锥Y+,且Y+≠Y,0∈Y+．Y+0表示Y+的内部,在Y中建立序关系：y≥y′⇔y-y′∈Y+, y≤y′⇔y′≥y；y＞y′⇔y-y′∈intY+,y＜y′⇔y′＞y．Y的拓扑对偶用Y∗表示，正锥Y+的对偶锥Y+∗={y∗∈Y:＜y,y∗＞≥0，∀y∈Y+}，其中＜y,y∗＞表示连续线性泛函y∗在点y的值．

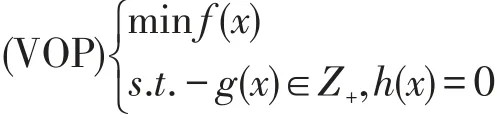
其中f:X→Y,g:X→Z,h:X→W均为Frechet可微函数．Z和W均为Banach空间，Y、Z、W都具有拓扑内部非空的正锥Y+,Z+,W+，并且W+还是点锥.K表示(VOP)的可行集，即：K={} x∈X:[g(x)≤0,h(x)=0]．

定义1[5]称BZ_5_1844_2534_1878_2573为(VOP)的弱有效解，如果不存在x∈K使得：f(x)＜f(BZ_5_1844_2534_1878_2573)．

设φ：X→Y，在BZ_5_1844_2534_1878_2573∈X处F可微，对于给定的函数η,θ:X×X→X，ρ∈Y，可以定义以下几种广义凸性函数．

定义2[5]称φ(关于Y+)在BZ_5_1844_2534_1878_2573是广义ρ-不变凸的，如果

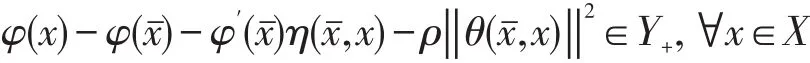
考虑无穷维最优化问题：

定义3[5]称φ(关于Y+)在是广义ρ－伪不变凸的，如果

定义4[5]称φ(关于Y+)在BZ_5_1844_2534_1878_2573是广义 ρ－拟不变凸的，如果

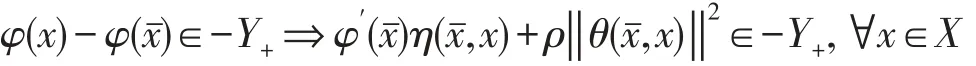
2 最优性充分条件

如果对(VOP)中的等式约束函数h(x)不附加任何的限制，则有如下定理：

又设f,g,关于相同的η,θ在BZ_5_1844_2534_1878_2573处分别为广义 ρ-不变凸的，广义σ-不变凸的，且

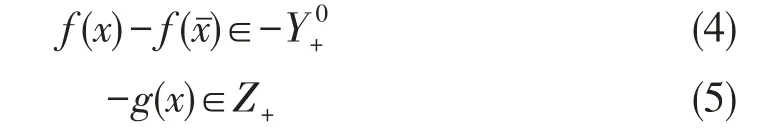
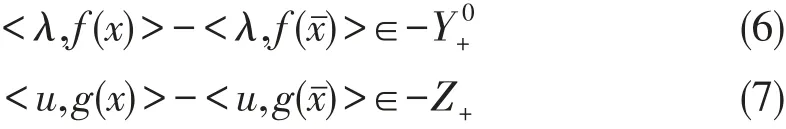
又利用f,g,的广义凸性知：

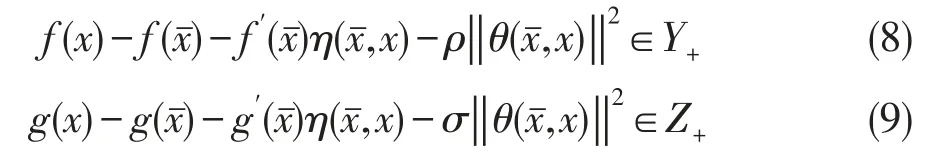
用λ、u依次作用于(8)式和(9)式得：

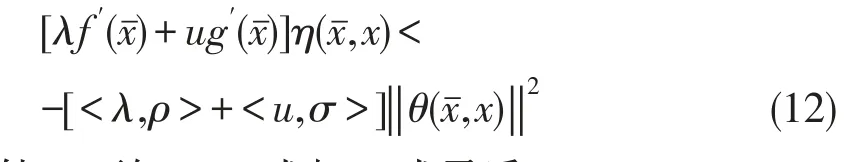
由条件(3)可知，(12)式与(1)式矛盾．

注：由于f在BZ_5_1844_2534_1878_2573处广义ρ-不变凸⇒f在BZ_5_1844_2534_1878_2573处广义ρ-伪不变凸⇒f在BZ_5_1844_2534_1878_2573处广义ρ-拟不变凸．所以将以上定理中的广义不变凸的条件相应地改成广义伪不变凸或广义拟不变凸，结论依然成立．

如果对(VOP)中的等式约束函数h(x)和不等式约束函数g(x)均不附加任何的限制，则有如下定理：

定理2.2设BZ_5_1844_2534_1878_2573∈K，若

将(10)式和(11)式相加并结合到(6)(7)两式得：，使得λf′(x)=0成立，f关于相同的η,θ在BZ_5_1844_2534_1878_2573处分别为广义ρ-不变凸的，且＜λ,ρ＞≥0，则BZ_5_1844_2534_1878_2573为(VOP)的弱有效解．

证明：假设BZ_5_1844_2534_1878_2573不是(VOP)的弱有效解，则∃x∈K,使得(4)式成立．

用λ作用于(8)式知(10)式成立．

结合(6)式及(10)式有：

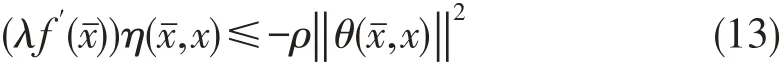
定理2.3设BZ_5_1844_2534_1878_2573∈K，若使得λf′(x)=0成立，λf关于相同的η,θ在处分别为广义ρ-不变凸的，且ρ≥0，则BZ_5_1844_2534_1878_2573为(VOP)的弱有效解．

证明：同定理1的证明知(4)式及(6)式成立．

又有λf的广义凸性条件知：

结合(6)式及(14)式有：

而λf′(x)=0及＜λ,ρ＞≥0与(13)式矛盾．

而λf′(x)=0及ρ≥0与(15)式矛盾．

[1]Li Z M.A theorem of alternative and its application to the optimization of set-valued maps[J].Journal of Optimization Theory and Application, 1999,100(2):365-375.

[2]Li Z M.The optimality conditions for vector optimization of set-valued maps[J].Journal of Mathematical Analysis and Applications,1999,273: 413-424.

[3]李泽民.半无穷向量最优化问题的最优性条件[J].系统科学与数学, 1994,14(4):375-380.

[4]陈光亚.Banach空间中向量极值问题的Lagrange定理及Kuhn-Tucker条件[J].系统科学与数学,1983,3(1):62-70.

[5]卢力,黄正海.Banach空间中向量最优化问题的充分条件[J].武汉城市建设学院学报,1996,13(2):69-75.

[6]蒋娅.锥约束向量最优化问题的弱有效解的一些充分条件[J].宜宾学院学报,2008(12):16-17.

[7]蒋娅.无穷维向量优化问题的弱Pareto最优解的充分条件[J].乐山师范学院学报,2009(5):14-15.

[8]蒋娅.一类集值映射向量优化问题的最优性条件[J].四川理工学院学报:自然科学版,2009(6):32-34.

【编校：许洁】

Kuhn-Tucker Optimality of Weakly Efficient Solutions for a Kind of Vector Optimization Problems

JIANG Ya
(College of Mathematics and Information,China West Normal University,Nanchong,Sichuan 637002,China)

Using some concepts of generalized convexity in Banach spaces,the Kuhn-Tucker sufficient condition of weakly efficient solutions for a kind of vector optimization problems was obtained.The results improve and extend some of the existing results in the literature.

weakly efficient solutions;sufficient optimality conditions;generalρ-inconvexity;generalρ-pseudo-inconvexity; ρ-quasi-inconvexity

O224

A

1671-5365(2014)06-0001-02

2013-11-10修回：2013-11-29

教育部科学技术重点项目(211163)；西华师范大学校基金青年项目(11A030)

蒋娅(1982-),女,讲师,硕士,研究方向为优化理论及应用

时间：2013-12-13 10:05

http://www.cnki.net/kcms/detail/51.1630.Z.20131213.0836.003.html