能量估计在偏微分方程中的应用
杜保营
(宜宾学院数学研究所,四川宜宾644007)
能量估计在偏微分方程中的应用
杜保营
(宜宾学院数学研究所,四川宜宾644007)
介绍了一般形式二阶n维双曲型方程初边值问题解的能量估计、一般形式二阶n维抛物型方程初边值问题解的能量估计以及一般形式二阶n维椭圆型方程边值问题解的能量估计,探讨了能量估计在这几类方程的(初)边值问题的一些应用,并得出一些结论.关键词:能量估计;双曲型方程;抛物型方程;椭圆形方程
能量估计又称能量不等式,它在偏微分方程中有着广泛的应用.曹洪锋等[1]研究了热传导方程中能量估计的一些应用;杨金林[2]研究了二阶波动方程中的能量估计与应用.一些特殊的偏微分方程的初边值问题解的唯一性和稳定性可用极值原理[3]或最大模估计[4]来处理.但是对于一般形式n维双曲型偏微分方程的初边值问题解的唯一性和稳定性,一般形式的n维抛物型偏微分方程初边值问题解的唯一性和稳定性以及一般形式n维椭圆型偏微分方程边值问题解的唯一性和稳定性用极值原理或最大模估计处理就会很困难,而用能量估计处理这几类偏微分方程解的唯一性及稳定性就能够很好地解决.本文就能量估计在这几类偏微分方程中的应用做一些探讨,并得出一定的结论.
1 基本概念
定义1[5]设Ω是Rn中的一个子集,u是Ω上的可测函数,而且|u(x)|p在Ω上可积,这种函数的全体记做Lp(Ω),即

Lp(Ω)称为Ω上的p方可积函数空间.在Lp(Ω)中定义范数如下

定义2[5]在定义1中,若p=2,则
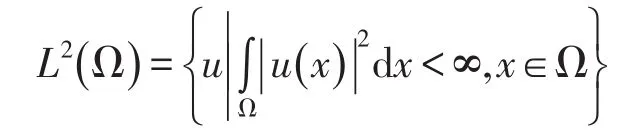
在L2(Ω)中定义范数为

定义3[6]设T>0,Ω为Rn中的一个可测集,则中的范数如下定义

引理1(Green公式)[7]三维空间有界闭体Ω是由光滑或逐片光滑的闭曲面Γ围成,函数P(x,y,z),Q(x,y,z),R(x,y,z)及其偏导数在有界闭体Ω上连续,则
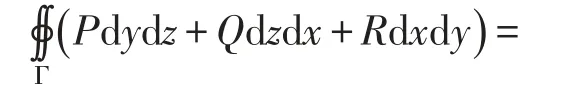
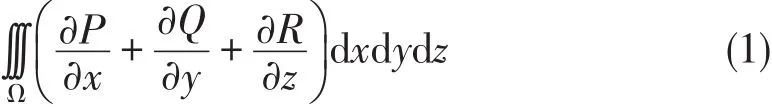
(1)式的另一种形式为

其中dΩ是Ω的体积微元,n是Γ的外法线方向,ds是Γ的面积微元.偏微分方程中常用Green公式的(2)式,该公式可以推广到有限维的形式.
2 双曲型方程中能量估计的应用
设Ω为Rn中的有界区域,且具有光滑边界Γ.T>0,在区域QT=Ω×() 0,T中考察一般形式的二阶双曲型方程

其中系数满足以下两个条件:
①系数aij,bi,b0,c及右端项f都是-QT上的连续函数,且aij在上具有一阶连续偏导数.
②对一切i,j=1,2…n,成立aij=aji,且存在正常数α>0,使得对一切及任意实向量都有
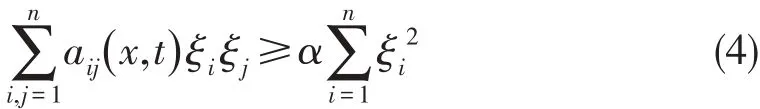
现在给定如下初始条件和边界条件:

其中ΣT=Γ×() 0,T为QT的侧边界.在双曲型方程初边值问题(3)(5)(6)引入该问题的能量函数:
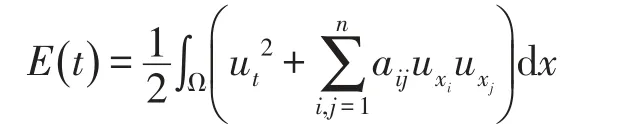
对(3)两边同时乘ut并在Ω上关于x积分,利用Green公式及Friedrichs不等式[6],可得到双曲型方程初边值问题(3)(5)(6)如下能量估计.
引理2[3]设u是双曲型方程初边值问题(3)(5)(6)的解,则成立下面的能量估计

其中c是一个不依赖于u的正常数.
定理1双曲型方程初边值问题(3)(5)(6)的解是唯一的.
证明:考察下面的双曲方程的初边值问题
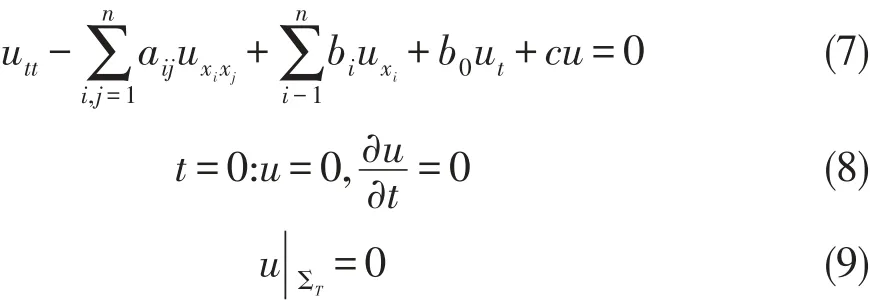
令

其中α为(4)式中的α.设u是双曲型方程初边值问题(7)(8)(9)的解,则
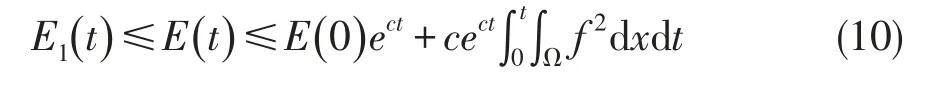
在双曲型方程初边值问题(7)(8)(9)中
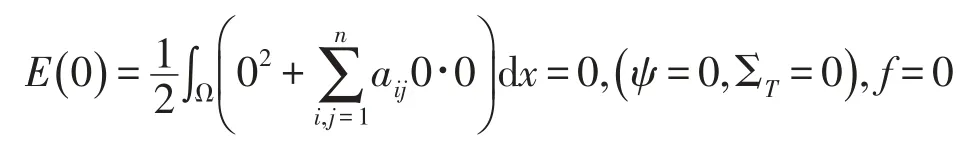
在不等式(10)中右端项为零,即E1(t)≤0,又E1(t)≥0,所以E1(t)=0.故ut=uxi=0,i=1,2…n.
所以u=const,又u(x,0)=0,因而u≡0,即双曲型方程初边值问题(7)(8)(9)的解必为零解.
设u1,u2为双曲型方程初边值问题(3)(5)(6)的任意两个解,则u=u1-u2为双曲型方程初边值问题(7)(8)(9)的解,所以u=0,即u1=u2.定理证毕.
定理2双曲型方程初边值问题(3)(5)(6)的解连续依赖于初始资料及右端项(关于初始资料及右端项具有稳定性).

即
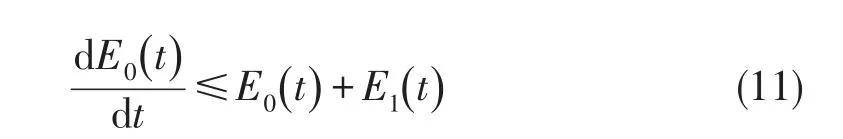
其中E1(t)为定理1证明过程中所设.以e-t同乘(11)式两边,并在0到t积分,整理得
又

即
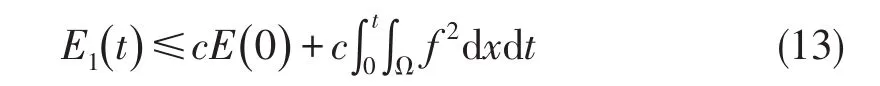
(12)+(13)整理得

又
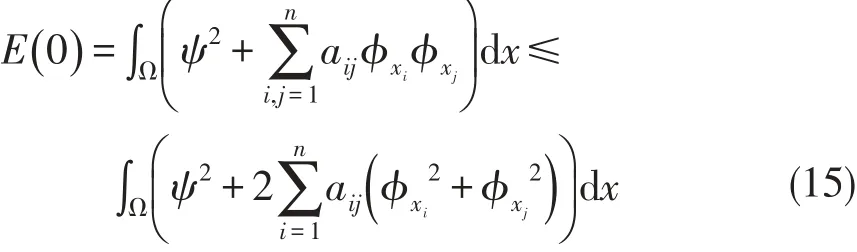
由(14)(15)整理得
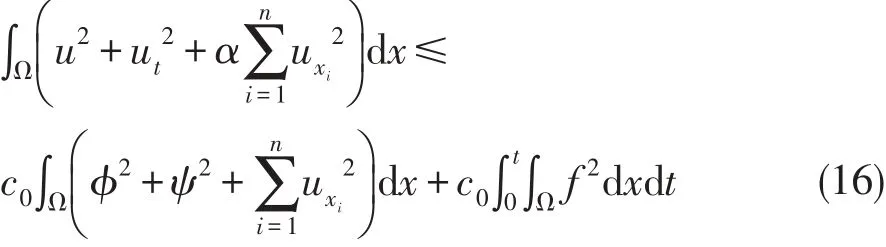
其中c,c1,c0是正常数.设u1是以φ1,ψ1,f1为初始资料和右端项的解,设u2是以φ2,ψ2,f2为初始资料和右端项的解,则u1-u2是以φ1-φ2,ψ1-ψ2,f1-f2为初始资料和右端项的解,由(16)式可知:∀ε>0,∃仅依赖于ε,T的η>0,只要
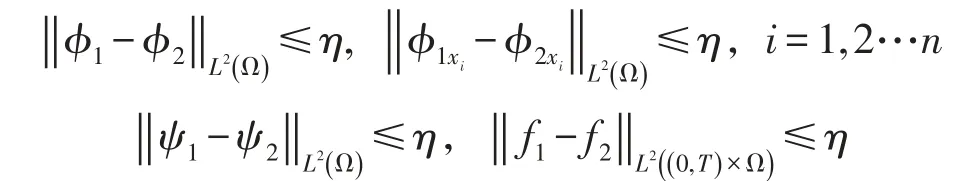
就有
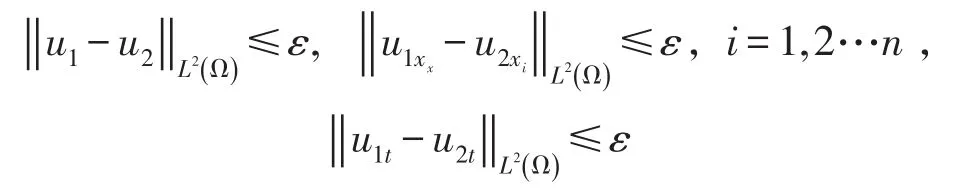
定理证毕.
3 抛物型方程能量估计的应用
在QT中考察下面的二阶抛物型方程

其中系数及右端项仍满足前面双曲型方程的条件①②.方程(18)满足下面的初始条件及边界条件:

引理3[3]设u抛物型方程初边值问题(17)(18)(19)的解,构造能量函数则成立能量估计式:

其中c是一个不依赖于u的正常数.
定理3抛物型方程初边值问题(17)(18)(19)的解是唯一的.
证明:考察下面的抛物型方程的初边值问题


设u是抛物方程初边值问题(20)(21)(22)的解.则

在抛物方程初边值问题(20)(21)(22)中
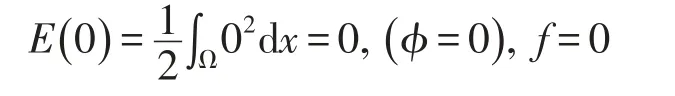
在不等式(23)中右端项为零,即E(t)≤0,又E(t)≥0,所以E(t)=0.故ut=uxi=0,i=1,2…n.所以u=const.
又u(x,0)=0,因而u≡0.即抛物方程初边值问题(20)(21)(22)的解的解必为零解.设u1,u2为抛物型方程初边值问题(17)(18)(19)的任意两个解,则u=u1-u2为抛物型方程初边值问题(20)(21)(22)的解,所以u=0,即u1=u2.定理证毕.
定理4抛物型方程初边值问题(17)(18)(19)的解连续依赖于初始资料及右端项(关于初始资料及右端项具有稳定性).
证明:设u抛物型方程初边值问题(17)(18)(19)的解,由引理3知:
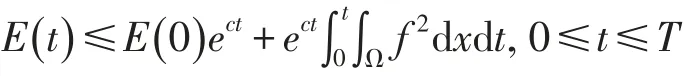
即

整理得

其中c1是正常数.设u1是以φ1,f1为初始资料和右端项的解,设u2是以φ2,f2为初始资料和右端项的解,则u1-u2是以φ1-φ2,f1-f2为初始资料和右端项的解,由(24)式可知:∀ε>0,∃仅依赖于ε,T的η>0,只要

就有
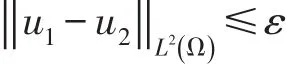
定理证毕.
4 椭圆型方程能量估计的应用
在Ω中考察下面的二阶椭圆型方程

其中系数及右端项仍满足前面双曲型方程的条件①②.方程(25)满足下面的边界条件:

引理4[3]存在一个仅依赖于区域Ω,α以及的最大值的正常数λ0,在c(x)≤-λ0时,椭圆型方程边值问题(25)(26)的解u,满足能量估计式:
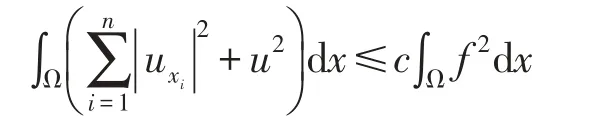
其中c是一个不依赖于u的正常数.
定理5椭圆型方程边值问题(25)(26)的解是唯一的.
证明:考察下面的抛物型方程的边值问题

设u是椭圆型方程边值问题(27)(28)的解.则由引理4知
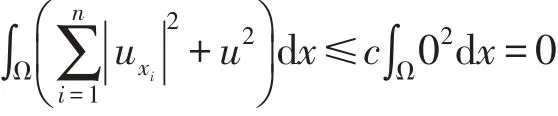
即

又
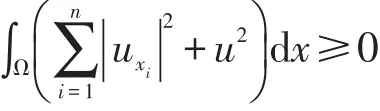
所以

故
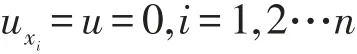
所以u(x)=0,因而u≡0.即椭圆型方程边值问题(27) (28)的解必为零解.设u1,u2为椭圆型方程边值问题(25) (26)的任意两个解,则u=u1-u2为椭圆型方程边值问题(27)(28)的解,所以u=0,即u1=u2.
定理证毕.
定理6椭圆型方程边值问题(25)(26)的解连续依赖于右端项(关于右端项具有稳定性).
证明:设u椭圆型方程边值问题(25)(26)的解,由引理4知:
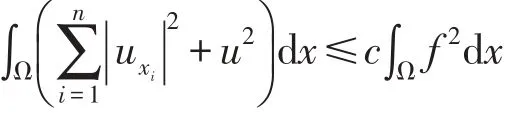
整理得:
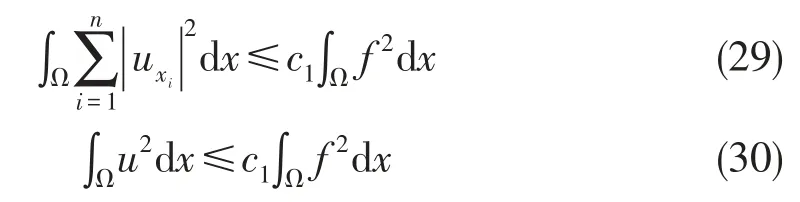
其中c1是正常数.设u1是以f1为右端项的解,设u2是以f2为右端项的解,则u1-u2是以f1-f2为右端项的解.由(29)(30)式可知:∀ε>0,∃仅依赖于ε的η>0,只要,就有
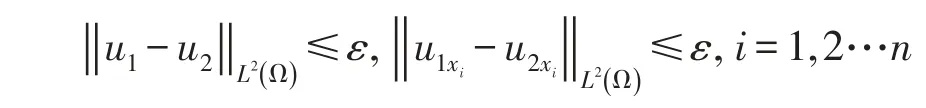
定理证毕.
5 结语
一些特殊的偏微分方程(初)边值问题解的唯一性和稳定性用(强)极值原理[8]处理会更容易,但是本文所讨论的一般形式n维偏微分方程(初)边值问题解的唯一性和稳定性的证明如果用(强)极值原理处理会很困难,而用能量估计处理就会容易很多.但是能量估计在偏微分方程中的应用也有一定的局限性,比如本文所讨论的三类方程系数和右端项必须要满足条件①②,边值条件必须为零等,椭圆方程还必须要满足引理4的条件.如果突破这些限制条件偏微分方程的(初)边值问题解的唯一性和稳定性是否仍成立,如果成立应该怎样证明?这些问题计划在以后的工作中研究解决.
[1]曹洪锋.热传导方程的能量估计[J].价值工程,2011(13):52-54.
[2]杨金林,杨勤荣.二阶波动方程的一种能量估计[J].包头钢铁学院学报,1996(4):34-36.
[3]谷超豪,李大潜,陈恕行,等.数学物理方程[M].第二版.北京:高等教育出版社,2002.
[4]崔志勇,金德俊,卢喜观.线性偏微分方程引论[M].长春:吉林大学出版社,1991.
[5]张恭庆,林源渠.泛函分析讲义:上册[M].北京:北京大学出版社, 1987.
[6]曹广福,严从荃.实变函数与泛函分析:下册[M].北京:高等教育出版社,2011.
[7]刘玉莲,傅沛仁.数学分析讲义:下册[M].第三版.北京:高等教育出版社,2001.
[8]陈恕行.现代偏微分方程导论[M].北京:科学出版社,2005.
【编校:许洁】
The Application of Energy Estimation in Partial Differential Equation
DU Baoying
(Institute of Mathematical Science,Yibin University,Yibin,Sichuan 644007,China)
The energy estimation of the initial boundary value in 2-order hyperbolic equations in the general form,in 2-order parabolic equations in the general form and in 2-order elliptic equations in the general form were introduced.Some application problems about the estimation of energy of the(initial)boundary value in these equations were discussed,then some conclusions were drawn.
energy estimation;hyperbolic equation;parabolic equation;elliptic equation
O175.2
A
1671-5365(2014)06-0003-04
2014-03-02修回:2014-03-05
宜宾学院科研启动项目硕士启动金(2012Q13)
杜保营(1981-),男,助教,理学硕士,研究方向为微分方程
时间:2014-03-27 17:44
http://www.cnki.net/kcms/detail/51.1630.Z.20140327.1744.005.html

