一类非线性分数阶微分方程边值问题正解的唯一性
古传运,郑凤霞
(四川文理学院数学与财经学院,四川达州635000)
一类非线性分数阶微分方程边值问题正解的唯一性
古传运,郑凤霞
(四川文理学院数学与财经学院,四川达州635000)
利用τ-φ-凹算子的不动点定理,研究了一类非线性分数阶微分方程边值问题正解的唯一性.主要结论不仅保证了正解的存在唯一性,而且能够构造一迭代序列去逼近此解.
分数阶微分方程;边值问题;正解;唯一性;τ-φ-凹算子;不动点定理
分数阶微分方程广泛应用于现实生活的诸多领域,如物理、力学、工程、化学、生物学和经济学等[1-3].近年来,众多专家学者利用锥上的不动点定理和Leray-Schauder理论等,深入研究了带有各种边值问题的非线性分数阶微分方程正解的存在性和多重性,并取得了重要的研究成果[4-7].
Xu等人[8]利用非线性leray-schauder选择定理、锥上的不动点定理等研究了非线性分数阶微分方程边值问题

正解的存在性,其中Dα0+是标准的α>0阶Riemann-Liouville分数阶导数.
受上述文献的启发,本文利用τ-φ-凹算子的不动点定理,研究如下非线性分数阶微分方程边值问题:

1 预备知识
定义1.1[2]对于定义在[0,∞)上的函数f(x),算式

称为标准的α>0阶Riemann-Liouville分数阶积分,等式的右端在[0,∞)有定义,其中Γ(α)表示Gamma函数.
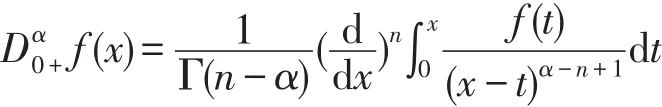
定义1.2[2]对于定义在[0,∞)上的函数f(x),算式称为标准的α>0阶Riemann-Liouville分数阶导数,等式的右端在[0,∞)有定义,其中n=[α]+1,[α]表示数α的整数部分.
引理1.1[8]给定h∈C[0,1]且3<α≤4.分数阶微分方程

其中:

这里称G(t,s)是分数阶微分方程边值问题(1.1)的Green函数,且

引理1.2[8]引理2.1中的Green函数G(t,s)具有如下性质:

其中M0=max{α-1,(α-2)2}.
下面再给出一些下文所要用到的序Banach空间中的一些基本概念和不动点定理,详细讨论可见文献[9, 10]及其他文献.
假设(E,‖∙‖)是实Banach空间,P为E中的非空闭凸子集,θ为E中的零元素.如果P满足(i)x∈P, λ≥0⇒λx∈P;(ii)x∈P,-x∈P⇒x=θ,则称P为E中的一个锥.由P引出E中的半序关系如下: x,y∈E,x≤y当且仅当y-x∈P.若x≤y且x≠y,则记作x<y.
记P0={x∈P|x为P的内点},如果P0非空,则称锥P为体锥.若存在常数N>0,使得对任意x,y∈E, θ≤x≤y,都有‖x‖≤N‖y‖,则称锥P是正规的,其中N叫做锥P的正规常数.易知,对任意正规锥,正规常数N≥1.若x≤y,就有Ax≤Ay,则称一个算子A:E→E是递增的.
任意x,y∈E,若存在λ>0和 μ>0,使得λx≤y≤μx,则称x~y.显然~是一个等价关系.给定w>θ(即w≥θ且w≠θ),记Pw={x∈E|x~w},易知当∀w∈P,有Pw⊂P且当w∈P0时,Pw=P0.
定义1.3[10]设P是实Banach空间E中的锥.A:P→P称为τ-φ-凹算子,如果存在两个定义在区间(a,b)上的正值函数τ(t),φ(t)使得τ:(a,b)→(0,1)是满射, φ(t)>τ(t),∀t∈(a,b)和A(τ(t)x)≥φ(t)Ax,∀t∈(a,b),x∈P.
引理1.3[10]设P是实Banach空间E中的正规锥.假设A:P→P是一个递增的τ-φ-凹算子和存在w∈P且w≠θ使得Aw∈Pw.则有:
(i)存在u0,v0∈Pw和r∈(0,1)使得rv0≤u0<v0, u0≤Au0≤Av0≤v0; (ii)算子方程Ax=x在Pw中存在唯一不动点x*;(iii)对任意初值x0∈Pw,构造一迭代序列xn=Axn-1,n=1,2,...,则当n→∞时‖xn-x*‖→0.
2 主要结果
利用引理1.3研究非线性分数阶微分方程边值问题(0.1),并得到关于其正解存在唯一性的新结果.
在本文中,所讨论的空间是Banach空间C[0,1],且赋有标准范数‖x‖=sup{|| x(t):t∈[0,1]}.注意到这个空间可以赋予偏序,定义为
∀x,y∈C[0,1],x≤y⇔∀t∈[0,1],x(t)≤y(t)令P={x∈C[0,1]|x(t)≥0,t∈[0,1]},显然P是Banach空间C[0,1]中的正规锥且正规常数是1.
定理2.1假设:
(H1)f(t,u):[0,1]×[0,∞)→[0,∞)关于u是连续递增函数且f(t,0)≡0;
(H2)存在两个定义在区间(0,1)上的正值函数τ(t),φ(t)使得τ:(0,1)→(0,1)是满射,φ(t)>τ(t),∀t∈(0,1)满足f(t,τ(λ)u)≥φ(λ)Au,∀λ∈(0,1),∀t∈(0,1),∀u∈P.则有:
(1)存在u0,v0∈Pw和r∈(0,1)使得rvo≤u0<v0且

其中w(t)=tα-2(1-t)2,t∈[0,1]和G(t,s)即为式(2.2).
(2)非线性分数阶微分方程边值问题(0.1)在Pw中存在唯一正解u*.
(3)对任意初值x0∈Pw,构造一迭代序列

从而当n→∞时有‖xn(t)-u*(t)‖→0.
证明:由引理1.1,问题(0.1)与下列的一个积分方程等价:

定义算子A:P→E为

容易证明u是问题(0.1)的解当且仅当u=Au.因为f(t,u(t))≥0,所 以 有Au(t)≥0,t∈(0,1),从 而A:P→P.下面验证算子A满足引理1.3的所有条件.
首先证明Aw∈Pw,其中w(t)=tα-2(1-t)2,t∈[0,1].
由条件(H1)和引理1.2,对于∀t∈[0,1],则有

从条件(H1)可知

因为f(t,0)≡0,∀t∈[0,1],所以

从而

因此l1w(t)≤Aw(t)≤l2w(t),t∈[0,1];故Aw∈Pw.
其次,从条件(H1)(H2)可知,对∀λ∈(0,1)和u∈P,有

即对于∀λ∈(0,1),u∈P,有A(τ(λ)u)≥φ(λ)Au.所以算子A是一个递增的τ-φ-凹算子.
最后,利用引理1.3可得:
(1)存在u0,v0∈Pw和r∈(0,1)使得rvo≤u0<v0且

其中w(t)=t(1-t),t∈[0,1]和G(t,s)即为式(1.2).
(2)非线性分数阶微分方程边值问题(0.1)在Pw中存在唯一正解u*.
(3)对任意初值x0∈Pw,构造一迭代序列

从而当n→∞时有

[1]Miller K S,Ross B.An introduction to the fractional calculus and fractional differential equations[M].New York:John Wiley,1993.
[2]Samko S G,Kilbas A A,Marichev O I.Fractional integral and derivatives:theory and applications[M].Switzerland:Gordon and Breach, 1993.
[3]Podlubny I.Fractional differential equations,mathematics in science and engineering[M].New York:Academic Press,1999.
[4]Zhao Y,Sun S,Han Z.The existence of multiple positive solutions for boundary value problems of nonlinear fractional differential equations [J].Commun Nonlinear Sci Numer Simulat,2011(16):2086-2097.
[5]Liang S,Zhang J.Existence and uniqueness of strictly nondecreasing and positive solution for a fractional three-point boundary value problem [J].Comput Math Appl,2011(62):1333-1340.
[6]Yang X,Wei Z,Dong W.Existence of positive solutions for the boundary value problem of nonlinear fractional differential equations[J].Commun Nonlinear Sci Numer Simulat,2012(17):85-92.
[7]Ding X,Feng Y,Bu R.Existence,nonexistence and multiplicity of positive solutions for nonlinear fractional differential equations[J].J Appl Math Comput,2012(40):371-381.
[8]Xu X,Jiang D,Yuan C.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation[J].Nonlinear Analysis,2009(71):4676-4688.
[9]Guo D.Fixed points of mixed monotone operators with application[J]. Appl Anal,1988(34):215-224.
[10]Zhai C B,Cao X M,Fixed point theorems for τ-φ-concave operators and applications[J].Computers and Mathematics with Applications, 2010(59):532-538.
【编校:许洁】
The Uniqueness of Positive Solution for a Class of Nonlinear Fractional Differential Equation Boundary Value Problem
GU Chuanyun,ZHENG Fengxia
(School of Mathematics and Finance-Economics,Sichuan University of Arts and Science,Dazhou,Sichuan 635000,China)
The uniqueness of positive solution for nonlinear fractional differential equation boundary value problem was concerned using the fixed point theorem forτ-φ-concave operator.The results can guarantee the uniqueness of positive solution, and can also be applied to construct an iterative scheme for approximating the solution.
fractional differential equation;boundary value problem;positive solution;uniqueness;τ-φ-concave operator; fixed point theorem
O175.8
A
1671-5365(2014)06-0013-03
2013-09-22修回:2013-10-25
四川文理学院校级科研项目(2012Z004Z)
古传运(1982-),男,助教,硕士,研究方向为应用数学
时间:2013-10-30 15:06
http://www.cnki.net/kcms/detail/51.1630.Z.20131030.1506.013.html

