大机动飞行的鲁棒自适应控制
周志久 刘 波 孙 勇
北京航天自动控制研究所,北京100854
大机动飞行的鲁棒自适应控制
周志久 刘 波 孙 勇
北京航天自动控制研究所,北京100854

针对飞机大机动飞行时存在的模型气动参数不确定性和外界扰动等影响因素,提出了一种基于反步法的鲁棒自适应滑模控制方法。基于反步的思想,适当选取李亚谱诺夫函数回馈递推得到不确定参数自适应律,并在最后一步结合线性滑模设计滑模控制器。对某飞机六自由度模型的大机动仿真验证了该方法的有效性。
大机动飞行;反步自适应;滑模控制
现代高性能飞机的一个主要特点是机动性和敏捷性,其中一个重要环节是在大机动下对飞机进行控制。在大机动飞行时,气动力和气动力矩均成明显的非线性特性,三轴惯性动力学严重耦合,不能采用常规的线性小扰动方程处理,必须采用非线性控制方法处理耦合的运动方程,才能保证飞行安全。
滑模变结构控制[1]能够实现解耦控制,而且由于滑动模态的存在,使它对外界干扰和参数摄动具有强鲁棒性,已被用于非线性飞行控制系统的设计[2],但是系统的不确定性要满足匹配条件[1],而飞机在大机动时不确定性往往是不匹配的。
反步法[3]是20世纪90年代出现的自适应控制方案,是一种由前往后递推的设计方法,以Lyapunov能量函数的收敛性为目标,设计过程中保留了系统中有用的非线性特性,既可以处理匹配不确定性又可以处理非匹配不确定性,且具有良好的过渡过程品质,然而,反步法要求系统确定性满足可参数化表示的假设,且存在“计算膨胀”问题[3]。将滑模控制与反步控制方法相结合,既可以简化反步控制的“计算膨胀”问题[3],又增加了系统对非匹配不确定性的鲁棒性。
文中针对非线性飞机块严格反馈模型,将反步法与线性滑模相结合,设计了大机动飞行控制律。针对飞机模型中存在的气动参数不确定性、输入增益矩阵不确定性及未知有界干扰,基于Lyapunov稳定性理论,以一种递归的方式选取参数自适应律和滑模控制器。将所设计的飞控系统进行大机动仿真研究,结果证明该控制方案能控制飞机跟踪大机动指令飞行,且具有较强鲁棒性。
1 非线性飞机模型
本文的研究对象为战斗机六自由度非线性模型,控制目的是实现姿态输入指令φ,α,β的跟踪,因此主要考虑由φ,α,β,p,q,r,θ构成的姿态控制系统,数学模型如下[4]:

(2)
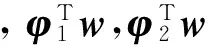
控制器设计的目的是在大机动时,在气动参数、控制增益矩阵未知及外界干扰存在的情况下,设计控制输入u,使得闭环系统的输出y(t)=(φ,α,β)T渐近跟踪期望的参考输入yd(t)=(φd,αd,βd)T。
2 控制器设计
为满足后续控制系统设计算法推导,在设计控制系统之前先给出如下的假设条件:


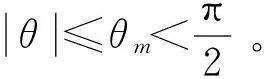
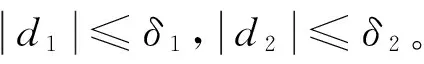
首先利用虚拟反馈定义跟踪误差状态变量,对于位置跟踪有
z1=y-yd=x1-x1d
(3)
z2=x2-x2d
(4)
其中,x2d为中间级虚拟控制变量。
对方程(3)求导得
(5)
为使每一状态分量具有适当的渐近特性,选择Lyapunov函数:
(6)
沿状态轨迹对式(6)求导得,
(7)
取中间级虚拟控制变量[5]
(8)
式中,k1是对称正定矩阵,a>0,ε>0。
将式(8)代入式(7)得
(9)
接下来与线性滑模相结合设计控制器,定义如下滑动流形
s=m1z1+z2,m1>0
(10)
对式(4)求导得
(11)
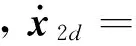
(12)
则
(13)
选择Lyapunov函数
(14)
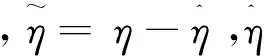
则
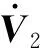
(15)
取参数自适应律为:
(16)
(17)
自适应滑模控制器:
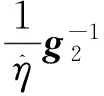
λsgn(s)+cs+m1v1s+v2s)
(18)
(19)
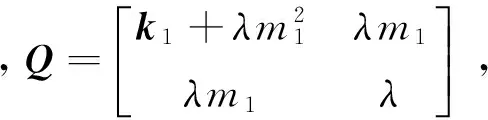
令
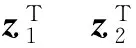
(20)
因此
(21)
对式(21)两边积分[6]得,
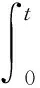
(22)
因此
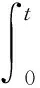
(23)
且
(24)
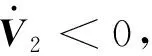
3 大机动飞行仿真


易见,即使存在较大的建模误差和外界扰动,控制系统仍能较理想地完成大机动动作,过渡过程良好,稳态侧滑小,鲁棒性强。图2是各个控制舵面偏转的仿真曲线,可见各个舵面变化均在限幅之内,未进入饱和状态。
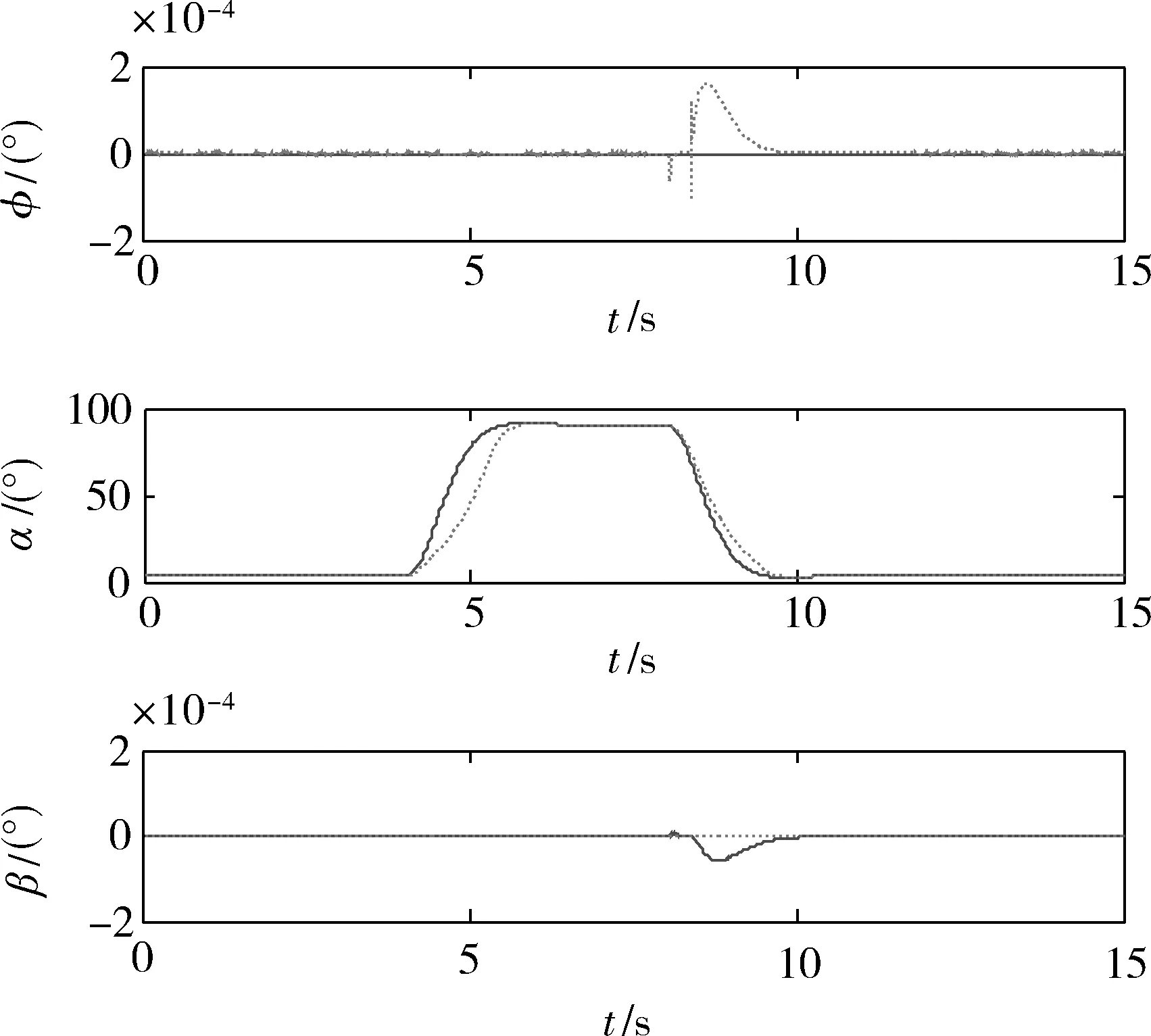
图1 φ,α,β响应曲线
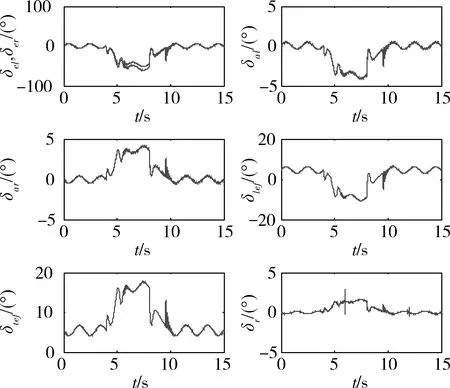
图2 控制舵面偏转曲线
注1:在大机动飞行时,常数空速的假设是不现实的,然而如果把空速也看作一个输出变量,油门控制可以添加作为一个控制输入来控制空速,文中的设计方法仍然适用。
注2: 由于滑模控制中不连续符号函数的引入,控制舵面存在抖振现象,可以在控制律式(18)中用sat函数取代符号函数消除控制抖阵。
4 结论
提出了一种基于反步法的鲁棒自适应滑模控制方法以解决大机动飞行时飞机非线性动力学模型具有的参数不确定性和不确定外部干扰问题。通过数值仿真,该控制系统可以理想地跟踪飞机大机动参考指令,具有较强的鲁棒性。
[1] 高为炳.变结构控制理论基础[M].北京:中国科学技术出版社, 1990,3.
[2] Shkolnikov I A, Shtessel Y B. Aircraft Nonminimum Phase Control in Dynamic Sliding Manifolds[J]. Journal of Guidance, Control and Dynamics, 2001,24 (3): 566-573.
[3] Krstic M, Kanellakopoulos I, Kokotovic P V. Nonlinear and Adaptive Control Design [M]. John Wiley & Sons Inc, New York, 1995.
[4] E R van Oort, L Sonneveldt, Q P Chu. A Comparison of Adaptive Nonlinear Control Designs for an Over-actuated Fighter Aircraft Model [C]. AIAA Guidance, Navigation and Control Conference and Exhibit,AIAA Inc, 2008.
[5] Ali J. Koshkouei, Alan S. I. Zinober. Adaptive Backstepping Control of Nonlinear Systems with Unmatched Uncertainty[C]. Proceedings of the 39thIEEE Conference on Decision and Control,2009: 4765-4770.
[6] 吴玉香,周东霞,胡跃明. 一类不确定非线性系统的鲁棒自适应控制[J].控制理论与应用,2008,25(6):1053-1058.(Wu Y X,Zhou D X,Hu Y M.Robust Adaptive Control of a Class Uncertain Nonlinear Systems[J].Control Theory & Applications,2008,25(6):1053-1058.)
[7] Slotine J E, Li W P. Applied Nonlinear Control[M]. Engle-wood Cliffs, New Jersey: Prentice Hall, 1991.
[8] S A Snell, D F Enns. Nonlinear Inversion Flight Control for a Supermaneuverable Aircraft[J]. Journal of Guidance, Control and Dynamics, 1992,15(4):976-984.
The Robust Adaptive Control for High Maneuvers Flight
ZHOU Zhijiu LIU Bo SUN Yong
Beijing Aerospace Automatic Control Institue,Beijing 100854, China
Arobustadaptiveslidingmodecontrollerbasedonbacksteppingisproposedforhighmaneuversflightregardingmodelparametersuncertaintiesandunknowndisturbance.TheuncertainparametersadaptivelawisobtainedrecursivelyviaanappropriatechoiceofLyapunovfunctionbasedonbacksteppingprocedure,andslidingmodecontrollerisdesignedwiththelinearslidingmodeinthelaststep.Thehighmaneuversflightsimulationresultsfornon-linear6-DOFaircraftmodelshowtheeffectivenessofthecontrolmethod.
Highmaneuversflight;Backstepping;Slidingmodecontrol
2013-01-25
周志久(1982-),男,烟台人,工程师,主要研究方向为控制系统综合设计;刘 波(1976-),男,山东青州人,高级工程师,主要研究方向为航天器控制系统综合设计;孙 勇(1984-),男,烟台人,工程师,主要研究方向为飞行器控制系统综合设计。
TP273;V249.1
A
1006-3242(2014)01-0035-05

