基于神经网络的再入自适应轨迹跟踪方法

张广勇 杨小龙 付维贤

北京宇航系统工程研究所，北京 100076



基于神经网络的再入自适应轨迹跟踪方法

张广勇 杨小龙 付维贤

北京宇航系统工程研究所，北京 100076

针对升力式再入飞行器的再入制导问题，根据设计得到的参考阻力加速度剖面，对动态逆阻力加速度跟踪原理进行分析，利用单隐层神经网络良好的非线性逼近能力，采用在线神经网络对逆误差进行补偿，并考虑气动参数偏差情况下的跟踪效果进行对比。针对参考阻力加速度变化剧烈而导致控制输入饱和的问题，本文引入PCH(Pseudo-control Hedging)思想，通过修正参考模型把参考信号限制在控制输入可实现的范围之内。仿真结果表明，该方法跟踪精度较高，可一定程度上缓解控制输入饱和。

再入制导；阻力加速度；神经网络；PCH

升力式再入飞行器再入制导分为纵向制导和侧向制导2个部分[1]。其中纵向制导主要通过航程预测来生成参考阻力加速度剖面，并通过跟踪参考阻力加速度得到控制量，阻力加速度的跟踪精度决定了飞行器的纵向制导精度。阻力加速度状态方程是一个强非线性的快时变系统，采用动态逆方法[2]设计跟踪控制律，可以跟踪参考阻力加速度得到倾侧角指令,且控制律对于环境参数变化有一定的自适应性，但是存在2个问题：1)鲁棒性较差，由于飞行参数的未知偏差以及不可预知的外部干扰，使跟踪效果变差；2)由于飞行器建模本身会存在误差，动态逆方法对模型的精确性依赖较强，逆误差会导致跟踪精度不高。

为了弥补上述不足，文献[3]考虑了常规的PID补偿，并分析了各型干扰下的跟踪误差，大幅提升了跟踪精度，但在文中提到了输入饱和导致跟踪误差的问题。文献[4-5]均采用神经网络对逆误差进行补偿，仿真结果表明该方法跟踪误差较小，但其参考阻力加速度均较光滑，并未遇到文献[3]中提到的问题。参考阻力加速度一般是离线设计或者在线规划得到的，无论哪种方式均有可能出现参考阻力加速度剧烈变化的情况，所以在设计跟踪控制律时必须考虑输入饱和的问题。PCH[6-8](Pseudo-control Hedging)思想是根据输入饱和状态修正参考模型使指令信号适应控制输入约束，达到缓解输入饱和的目的。

本文在基于动态逆阻力加速度跟踪的基础上，引入神经网络对动态逆误差进行补偿，并通过在线更新神经网络权值的方法来确保其动态补偿效果，最后采用PCH方法通过修正参考模型来防止控制机构进入饱和状态。仿真结果表明，基于神经网络的阻力加速度跟踪方法跟踪精度较高，鲁棒性能较好，PCH方案在一定程度上缓解了控制输入饱和问题。

1 阻力加速度再入制导原理

再入过程中，假设地球为圆球形，飞行器为刚体，仅受升力、阻力和重力的作用，飞行器运动方程组可表示为[9]

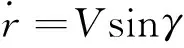
(1)

式中：r是飞行器地心径向距离，r=R0+h，h是飞行器当前高度，R0是地球平均半径；θ和φ分别是飞行器当前的经度、纬度；V是当前的速度；γ表示弹道倾角，ψ是航迹偏角；L和D分别是飞行器的升力加速度和阻力加速度;α和σ分别是攻角和倾侧角，作为控制输入量。

升力加速度和阻力加速度的表达式如下

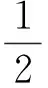
(2)

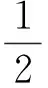
(3)

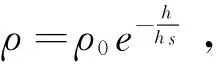
再入过程中射程的变化率为

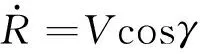
(4)

由式(1)可得

(5)

再入初期，由于飞行器的速度较大，速度倾角较小，故可认为γ为小量，有cosγ≈1,sinγ≈0，则

(6)

由式(6)可知，根据指定的射程要求，同时考虑再入过程中的热流、动压、过载、平衡滑翔等约束条件，可以在线给出参考的阻力加速度剖面，跟踪阻力加速度即可实现对射程的精确控制。

对式(3)求二阶导数

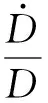
(7)

(8)

由式(1)可得

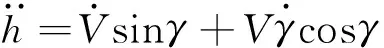
(9)

(10)

整理得

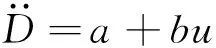
(11)

其中

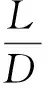
一般攻角α是根据飞行任务和再入约束事先给定的，因此控制量只有倾侧角σ。也可以将攻角α和侧滑角σ同时作为控制量进行协同控制，本文不对这种方法进行研究。考虑到建模过程中各项误差的存在，式(11)更准确的表达式应该为

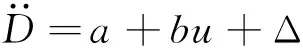
(12)

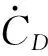
图1 基于神经网络的动态逆控制结构图

2 自适应跟踪控制律设计

根据动态逆控制原理，对式(11)的控制律可取为

u=b-1(υ-a)

(13)

其中，υ为伪控制量，代表系统期望的动态响应，与状态量之间有如下关系

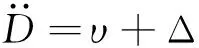
(14)

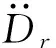
υ=υc+υk-υad

(15)

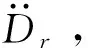
(16)

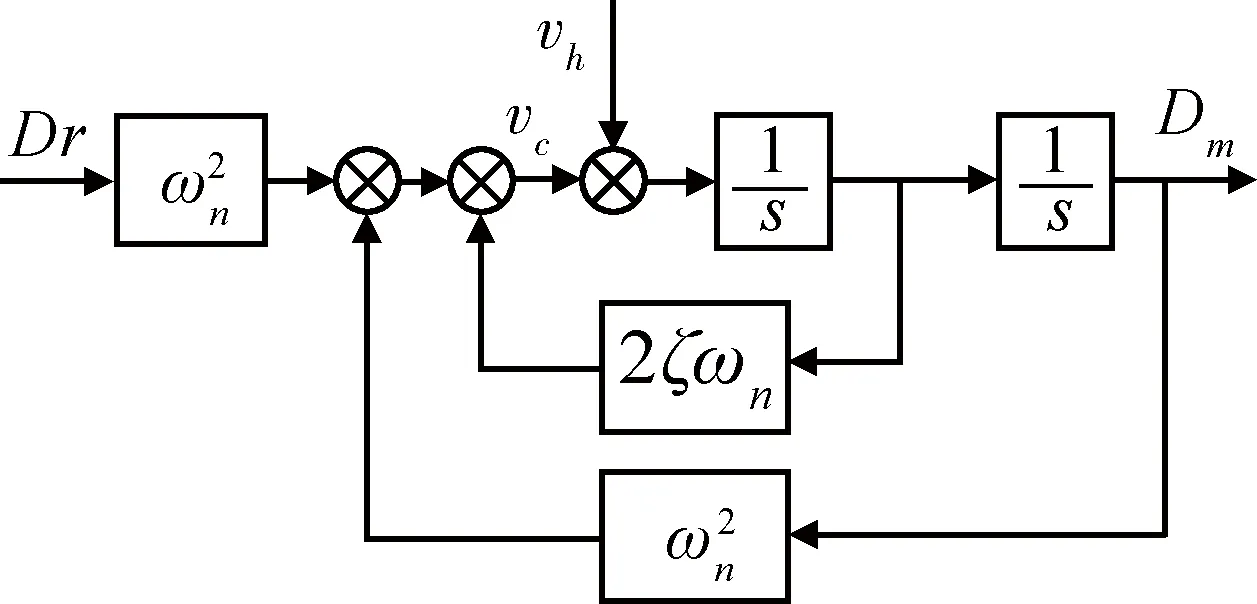
图2 参考模型结构图

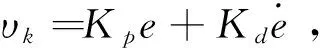
(17)

通过合理选择系数Kp,Kd，使矩阵A成为Hurwitz矩阵。理想情况下，若自适应项能够完全补偿逆误差，则系统跟踪误差以指数收敛于0。

单隐层神经网络结构图如图3所示。隐含层激励函数选择Sigmoid函数：

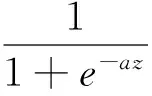
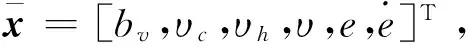
(18)

其中，W和V是相应维数的权值矩阵。

图3 单隐层神经网络结构图

定义矩阵Z和误差向量

其中，P为Lyapunov方程ATP+PA=-2I的正定解。选择鲁棒项为

(19)

为保证神经网络的实时控制特性，文献[8]采用在线更新神经网络权值方法，权值更新规则如下

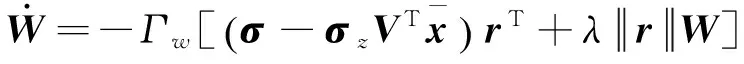
(20)

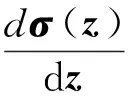
3 PCH控制律设计

PCH的概念最早是由Johnson提出的，旨在对于由控制机构位置限幅、速率限幅以及线性输入动态等输入特性引起的参考模型的不适应性进行修正来抑制或消除控制机构的饱和问题。PCH的一个优势是可使动态逆系统的相对阶降低一阶。动态逆方法可以对系统求逆，但是无法对以舵机为代表的输入特性求逆，PCH相当于给系统提供了一个额外的逆回路。

PCH方法的原理如下。对于动态系统动态逆控制律如下

δcomm=b-1(v-a)

得

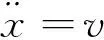
其中v为伪控制量。

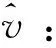
(21)

最终，可得PCH输出信号

(22)

该信号作为补偿信号反馈到参考模型中，则参考模型输出的指令信号变成

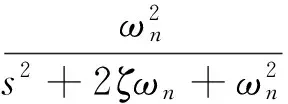
由上式可以发现，当控制指令在可实现范围内时，即vh=0，参考模型的输出会按照指定的动态性能跟踪指令信号；当控制指令超出可实现的范围时，通过PCH补偿可以对参考模型输出进行调整，将其控制在可实现的范围内。

4 仿真结果及分析

以X-33飞行器为对象进行再入制导仿真，以验证所研究方法的有效性。本文对仅含有PD补偿方案、含有PD和神经网络补偿方案以及含有PD、神经网络和PCH控制方案3种情况进行仿真。初始条件如下[r,θ,φ,V,ψ,γ]=[65km,0°,0°,6000m/s,0°,0°]。

式中，αmax，αmaxL/D分别为最大攻角和最大升阻比攻角；V0，Vf分别为再入点和滑翔段终点的速度；Va1，Va2为设计参数，由热约束与机动性权衡给出，文中选择Va1=5000m/s，Va2=3500m/s。

参考阻力加速度曲线如图4所示，其中细实线分别为动压、热流、过载和准平衡滑翔约束边界，粗实线为参考阻力加速度。容易看出，参考阻力加速度在3000m/s处有突变，此突变作用是验证PCH控制律的有效性。PD控制器的增益系数取为Kp=0.1，Kd=0.5。

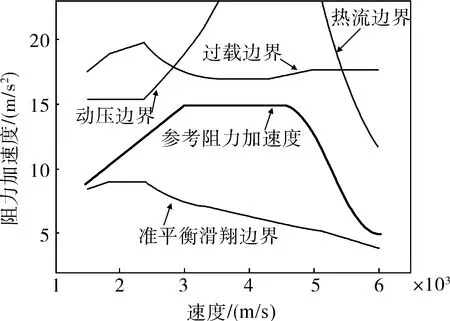
图4 参考阻力加速度曲线

不考虑气动偏差时仿真曲线如图5～7所示。图5为阻力加速度跟踪误差曲线1(Dm-D)，图6为阻力加速度跟踪误差曲线2(Dr-D)，图7为相应的倾侧角变化曲线。可以看出，加入神经网络补偿后，跟踪误差明显减小，但是在3000m/s处误差突然增大导致控制输入饱和，这是由于参考阻力加速度的突变造成的。加入PCH控制方案后图5中跟踪误差一直保持较小，图6中的跟踪误差变大，由于PCH在一定程度上修正参考模型的输出信号适应了控制输入的实际控制能力，但这是以牺牲跟踪精度为代价来换取控制机构的有效性和系统的稳定性。需要说明的是，本文考虑了初始误差，仿真结果也表明了所研究的方法收敛速度较快。

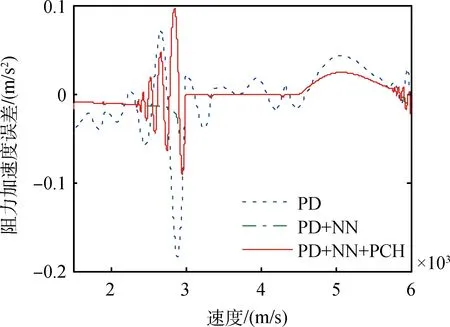
图6 阻力加速度跟踪误差曲线2

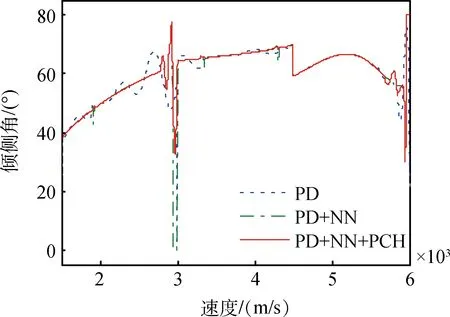
图7 倾侧角变化曲线

考虑气动参数40%的偏差，不考虑大气密度偏差的影响，仿真曲线如图9～10所示。其中图8为气动参数偏差情况下阻力加速度跟踪误差曲线1(Dm-D)，图9为气动参数偏差情况下阻力加速度跟踪误差曲线2(Dr-D)，图10为气动参数偏差下相应的倾侧角变化曲线。

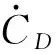
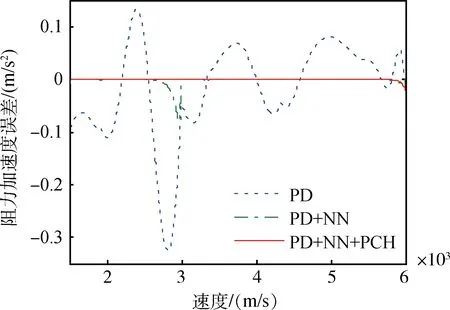
图8 气动参数偏差下阻力加速度跟踪误差曲线1

图9 气动参数偏差下阻力加速度跟踪误差曲线2

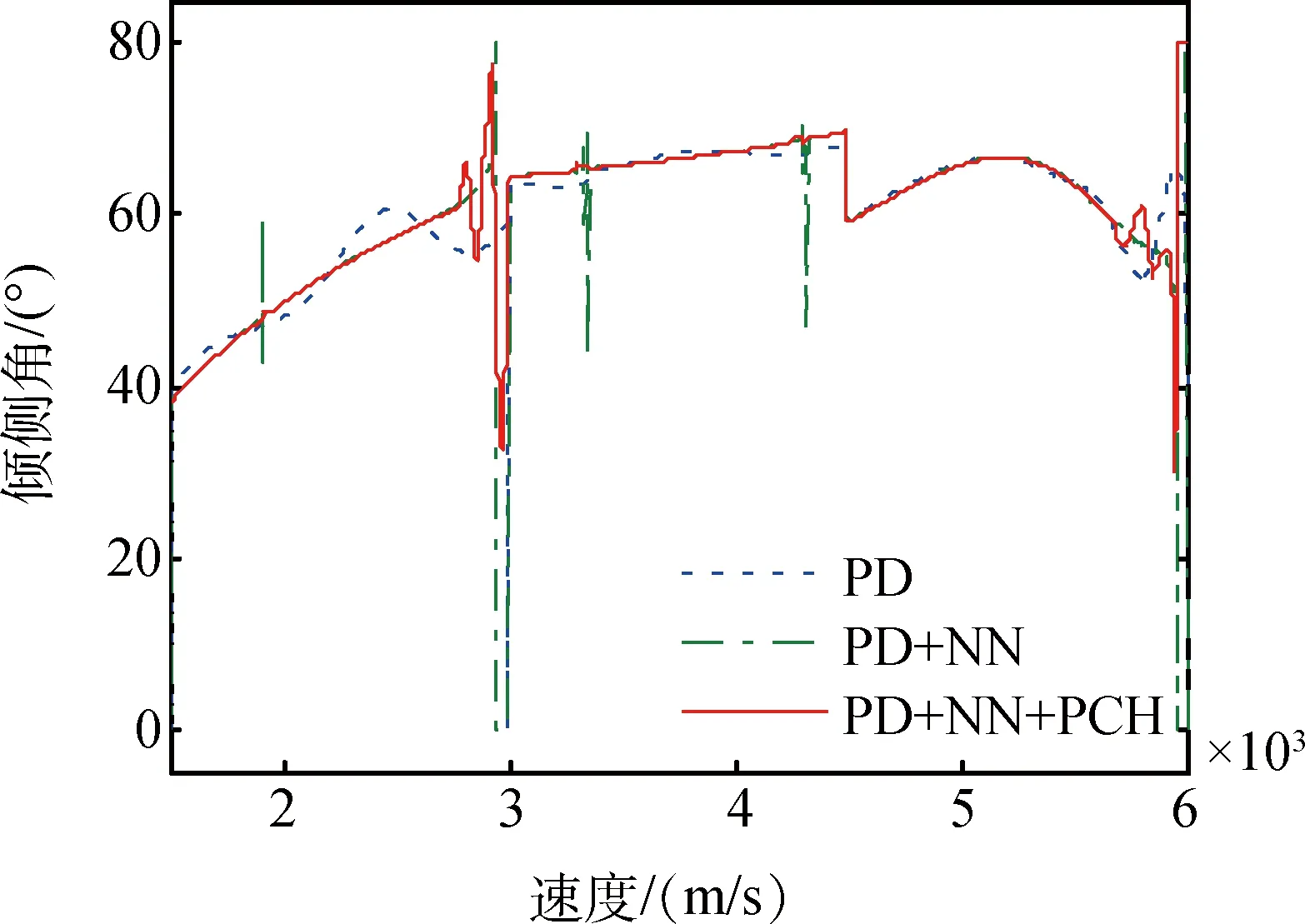
图10 气动参数偏差下倾侧角变化曲线

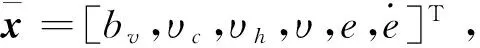
5 结论

研究了升力式再入飞行器的再入制导问题，针对动态逆方法依赖精确模型的问题，研究了基于神经网络的动态逆控制结构，利用神经网络对非线性函数的逼近能力和相应的控制律，实现了对参考阻力加速度的跟踪。针对参考阻力加速度剧烈变化而导致的控制输入饱和问题，本文引入了PCH控制方法。通过对X-33再入飞行器的阻力加速度跟踪制导仿真计算，结果表明本文所研究方法跟踪精度较高，PCH方案在一定程度上缓解了控制输入饱和问题。对于文中所提到的倾侧角出现高频振荡的问题，在后续的研究中需要更多关注神经网络输入项的选择。

[1] 赵汉元.再入飞行器动力学和制导[M].长沙：国防科技大学出版社，1997.(Zhao H Y. Dynamics and Guidance of Reentry Vehicle[M]. Changsha: National University of Defense Technology Press，1997.)

[2] Hall C E, Leavitt J A, Chen D T, et al. Design and Evaluation of an Acceleration Guidance Algorithm for Entry [J]. Journal of Spacecraft and Rockets, 2004, 41(6): 986-996.

[3] Yang Xiao-long,Mease K D.Entry Guidance and Trajectory Tracking Error Analysis[J].Journal of Astronautics, 2004, 25(3): 283-288.

[4] 郑总准，王永骥,等.基于FCMAC干扰观测器的动态逆再入制导[J].华中科技大学学报(自然科学版)，2010，38(1): 96-100.(Zheng Z Z, Wang Y J, et al. Dynamic Inversion Reentry Guidance Based on FCMAC Disturbance Observer for Lift Vehicle[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2010, 38(1): 96-100.)

[5] 吴浩，杨业.基于RCMAC网络的动态逆再入制导方法研究[J].空间控制技术与应用，2011，37(4): 49-53.(Wu H, Yang Y. Dynamic Inversion Reentry Guidance Based on RCMAC Network[J]. Aerospace Control and Application,2011, 37(4): 49-53.)

[6] Johnson E N, Calise A J. Pseudo-control Hedging: A New Method for Adaptive Control [C]. Advances in Navigation, Guidance and Control Technology Workshop, 2000.

[7] Johnson E N,Calise A J,J.Eric Corban.Adaptive Guidance and Control For Autonomous Launch Vehicles [J].IEEE,2001,(6): 2669-2682.

[8] Johnson E N,Calise A J.Neural Network Adaptive Control of Systems with Input Saturation [C].Proceedings of the American Control Conference, Arlington, Virginia,June 25-27, 2001: 3527-3532.

[9] Lu P and Hanson J M.Entry Guidance for the X-33 Vehicle [J].Journal of Spacecraft and Rockets, 1998, 35(3): 342-349.

[10] Lewis F L, Yesidirek A, Liu K. Multilayer Neural-net Robot Controller with Guaranteed Tracking Performance [J].IEEE Transactions on Neural Networks, 1996, 7(2): 388-399.

An Adaptive Reentry Trajectory Tracking Method Based on Neural Network

ZHANG Guangyong YANG Xiaolong FU Weixian

Beijing Institute of Space System Engineering，Beijing 100076，China

Aimingatthereentryguidanceproblemofliftreentryvehicle,thedynamicinversiondragaccelerationtrackingtheoryisanalyzedrestingonareferencedragacceleration-velocityprofiledesignedinadvance.Then,bytakingadvantageofthenonlinearapproximationability,onlineneuralnetworkisintegratedinthedynamicinversionmethodtocompensatetheinversionerror.Thetrackingabilityiscontrastedwiththatinthesituationofaerodynamiccoefficientdeviation.Byconsideringtheinputsaturationcausedbyabruptvariationofreferencedragacceleration-velocityprofile,thepseudo-controlhedging(PCH)methodisresearchedinthepaper.ThePCHcanhedgethereferencesignaldowntoalevelthatisachievablebytheactuatordynamics.Thesimulationresultsshowthatthismethodcantrackthereferencesignalpreciselyandhedgetheinputsaturationonacertainextent.

Reentryguidance；Dragacceleration；Neuralnetwork；PCH

2013-07-30

张广勇(1989-),男，河北邢台人，硕士研究生，主要研究方向为制导与控制系统总体设计；杨小龙(1967-)，男，山西阳泉人，主要研究方向为飞行器总体设计；付维贤(1960-)，女，北京人，研究员，主要研究方向为飞行器总体设计、控制系统总体设计与仿真。

V448.235

A

1006-3242(2014)01-0073-06