基于LMI的挠性航天器抗饱和补偿器设计及分析*
王明钊 刘金琨
北京航空航天大学自动化科学与电气工程学院,北京 100191
基于LMI的挠性航天器抗饱和补偿器设计及分析*
王明钊 刘金琨
北京航空航天大学自动化科学与电气工程学院,北京 100191

针对挠性航天器中输入受限问题,设计了基于LMI的抗饱和补偿器。理想情况下,挠性航天器采用LQG控制,保持系统闭环稳定;输入受限时,在不改变系统原有结构的前提下,设计基于LMI的抗饱和补偿器。抗饱和补偿器为静态补偿器,所以不增加系统阶数;它不仅保证系统能够闭环稳定,还能保证系统满足最优的L2指标。仿真表明,在理想情况和受限情况下,抗饱和补偿器均能保证系统闭环稳定,并且具有良好的鲁棒性。
输入受限;LMI;抗饱和;挠性航天器;补偿器
随着空间技术的不断发展与航天需求的不断增长,航天器的结构越来越复杂,尺寸也越来越大,但由于发射成本及运载能力限制的原因,航天器的重量成为一个严格的约束条件。在航天器姿态控制方面,飞轮等执行机构由于上述限制,只能提供有限的控制力矩,这就容易产生输入受限问题。该问题在某种程度上将影响航天器姿态控制精度,甚至使整个姿态控制系统不稳定。
近年来,国内外的学者对挠性航天器的抗饱和问题进行了深入研究,线性矩阵不等式(Linear Matrix Inequalities,简称LMI)作为一种有效的数学工具,被广泛应用于抗饱和控制领域中。文献[1]基于线性矩阵不等式法(LMI),针对线性系统提出了一种改进的抗积分饱和控制器来实现系统的稳定控制;文献[2]针对线性系统利用LIM方法设计补偿器,实现系统抗饱和目标。Mulder等[3]针对动态控制器,设计了静态补偿器,保证了系统全局稳定,并且降低了系统的L2增益。Grimm等[4]针对一般情况下的稳定模型系统设计了基于LMI的动态补偿器,保证系统稳定,并保证系统输出对外部干扰具有L2增益。Hu等[5-6]针对一般系统研究了L2增益的特性以及稳定区域。随后,Hu等[7]针对更普遍的稳定系统进行了补偿器的设计,并且对稳定区域和非线性性能指标进行了讨论。Hencey等[8-10]利用LMI区域法研究了抗饱和中D稳定问题。
针对挠性航天器中存在的输入受限问题,本文设计了基于LMI的抗饱和补偿器,保证了系统在输入受限情况下的闭环稳定。同时补偿器是静态的,没有增加系统的阶数。
1 挠性航天器控制系统描述
挠性航天器姿态角理想控制系统如图1所示。
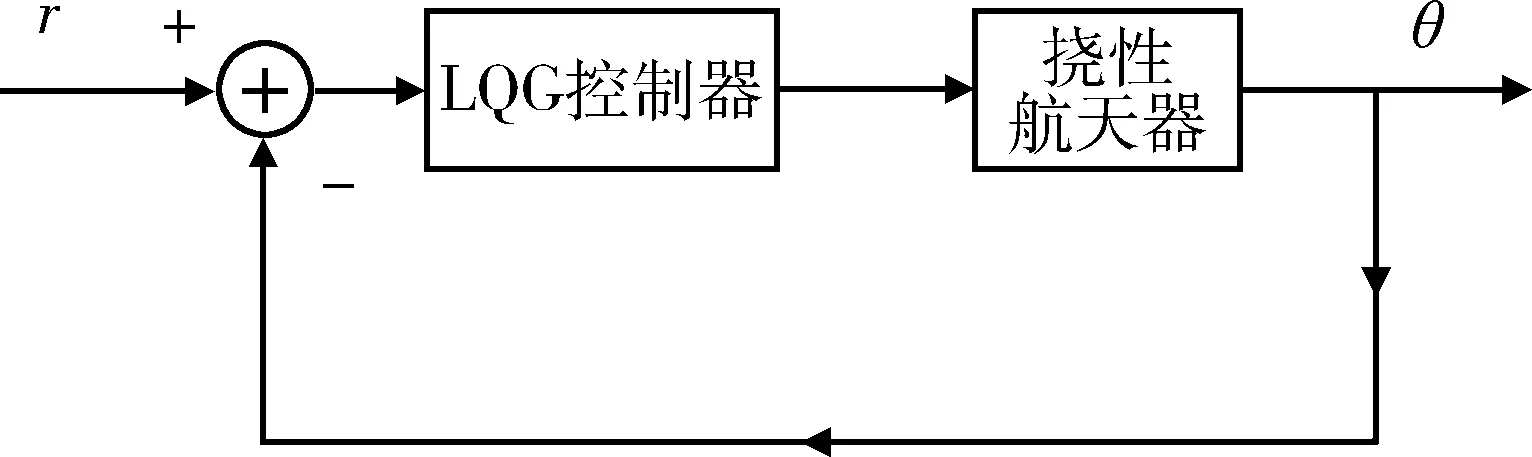
图1 挠性航天器理想控制系统图
挠性航天器的简化模型如下所示:
(1)

为了便于设计LQG控制器和补偿器,将式(1)写成状态方程、输出方程、误差方程标准形式:
(2)
根据式(2)设计挠性航天器的LQG控制器如下所示:
(3)
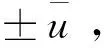
(4)
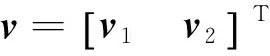
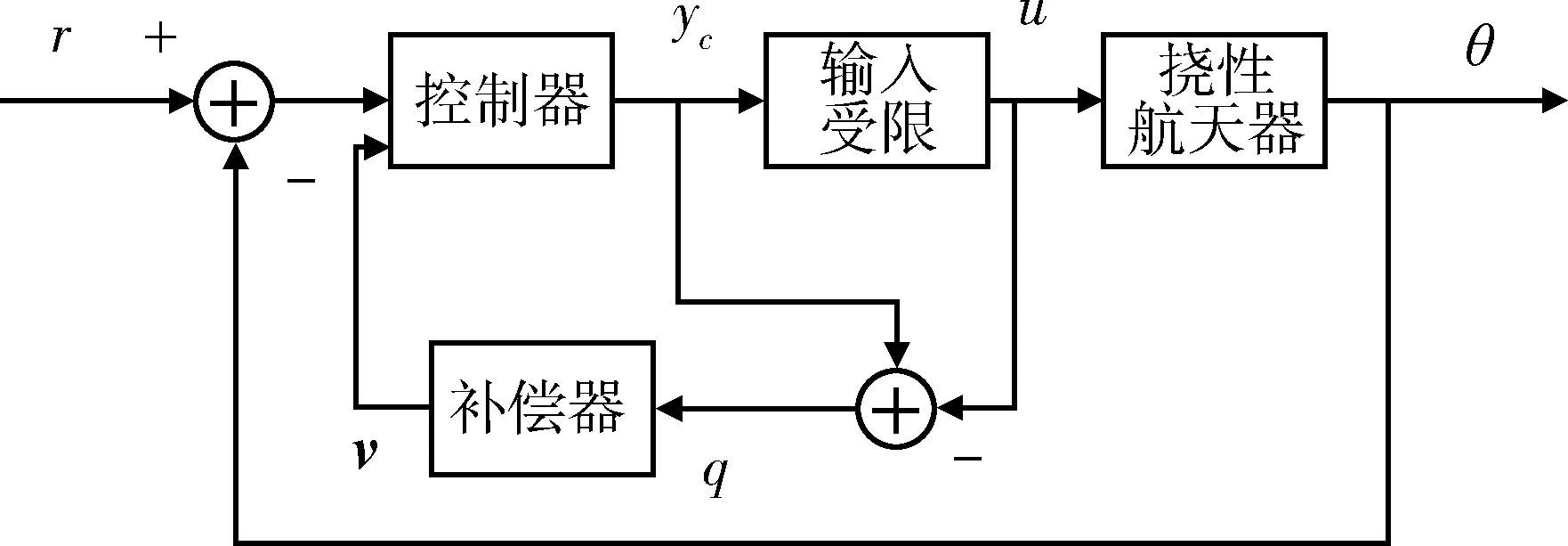
图2 挠性航天器输入受限控制系统
图2中受限系统的控制器如下所示:
(5)
2 基于LMI的补偿器设计
为了保证挠性航天器姿态角输入受限控制系统的稳定性,设计补偿器如下:
(6)
其中,q=yc-u。系统可表示成如下标准形式:
(7)
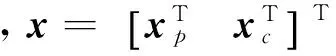
在本节中,将采用线性矩阵不等式(LMI)方法,证明存在补偿器,保证输入受限系统稳定。把补偿器(6)代入标准状态方程(7)中可得:
2.1 定义及引理
为了证明存在式(6)的补偿器,保证挠性航天器受限控制系统稳定,需要用到以下的定义和引理[6,11]。
定义1:设X为方形矩阵,则HeX:=X+XT。
引理1:对于系统(7),设矩阵Q∈Rn×n,Q=QT>0。
设γ>0,s>0。如果存在矩阵Y∈Rnu×n和对角矩阵U>0,满足以下条件:
(8)
(9)
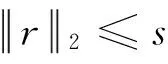
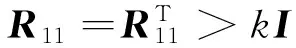
(10)
2.2 补偿器设计及存在性证明
根据下面的设计方法,利用MATLAB中的LMI工具箱,可以获得抗饱和补偿器式(6)。
(1)解不等式
利用MATLAB中的LMI工具箱,解下列不等式,得到解(R,Z,γ2)。其中,
(11)
(12)
(13)
(14)
(2)LMI求解补偿器
令m=n+nu+nr+nz,构造矩阵H∈Rnv×m,ΨR∈Rm×m和GU∈Rnu×m如下所示:
然后求解不等式:
(15)
其中,ΛU∈R(naw+nv)×(naw+nu),对角矩阵U∈Rnu×nu,U>0为不等式的未知变量。最后即可获得抗饱和补偿器:
Daw=AUU-1
(16)
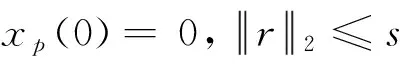
证明:根据设计方法中的第(1)步,LMI的解(R,Z,γ2)令式(12)成立。根据文献[4]的方法,构造一个特殊矩阵WH如下:
其中,WH的列向量分别为H零空间基向量组成,分块矩阵的前3×3块为(np+nw+nz)×n维。经过计算,式(12)可以写成如下形式:
令P=R-1,根据文献[4]方法可得:

根据文献[4]中的定理5,式(11)成立,当且仅当
同时成立。所以第(1)步中式(11)~(14)的解(R,Z,γ2)保证了式(15)必然有解。令Q=R,则式(9)与(15)相同,所以式(9)成立。
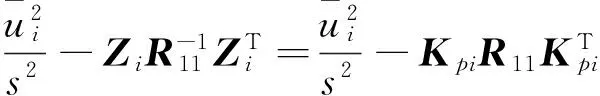
令Q=R,根据Schur补的性质,可以得到式(8)。
所以根据引理1,补偿器式(6)存在,且满足定理1的结论。
注:当模型(1)含有虚轴上的极点,且其余极点均在左半平面时,不等式(11)~(13)有解(R,Z,γ2)。由于系统是闭环指数稳定的,选择R=
RT>0满足
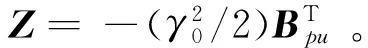
(17)
因此,对于任意s>0,可以选择足够大的R11满足式(17)及下式
当R11和Z满足上述条件时,总是能选择足够大的γ同时满足式(12)和(13)。
3 仿真结果
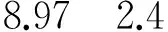

补偿器Daw如式(19)所示。此时闭环系统的有限L2增益为γ=1.9421。仿真结果如图3和4所示。

图3 挠性航天器姿态角输出(理想系统、输入受限系统、加入补偿器的受限系统)
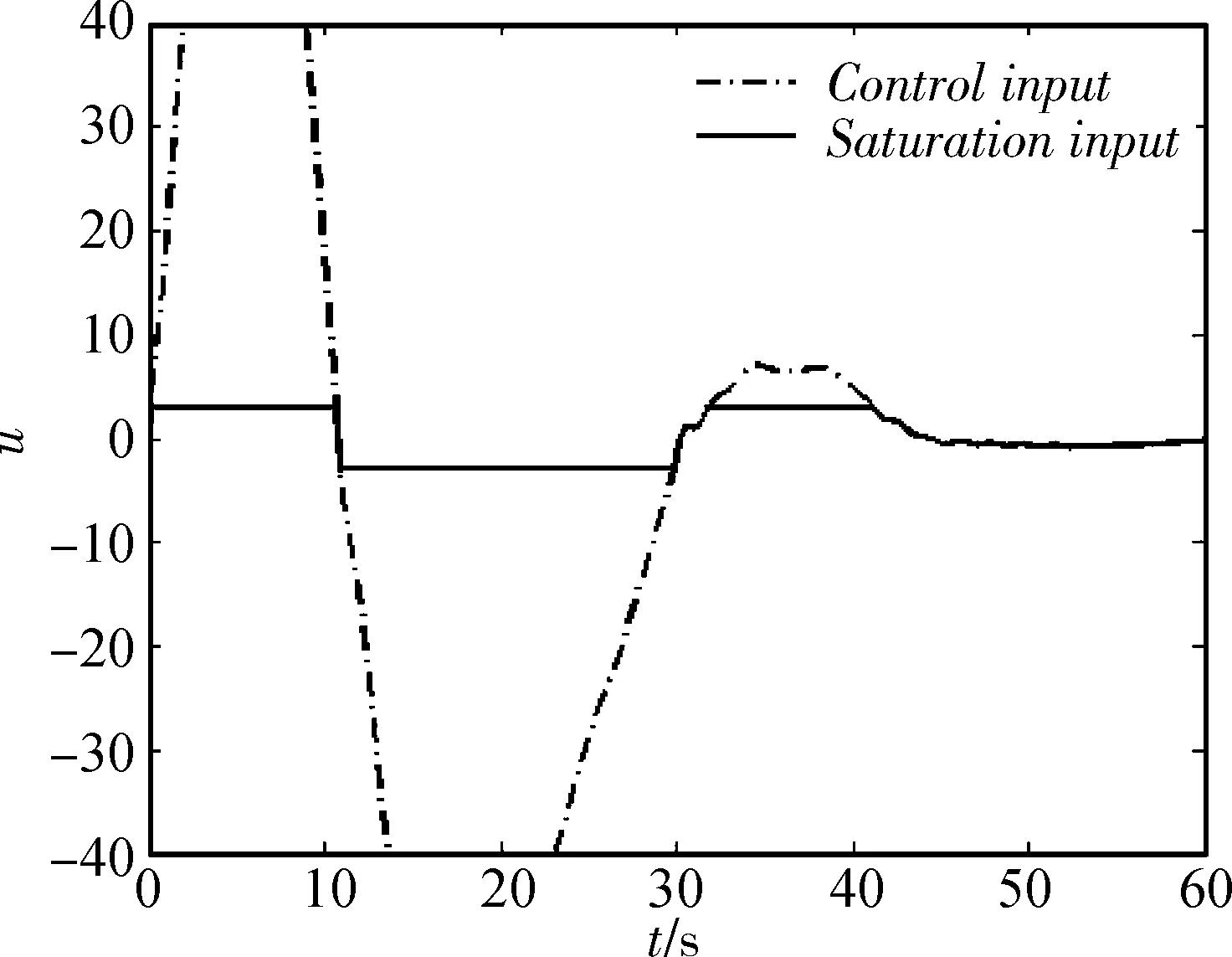
图4 LMI补偿器系统控制器输出及受限输出
根据图3,理想情况下,LQG能够保证系统的稳定性;存在输入受限时,系统无法保持稳定;加入LMI补偿器时,即使在受限情况下,系统仍能保持稳定。图4显示了理想情况下与受限情况下的控制信号变化情况。
4 结论
针对挠性航天器姿态角控制系统,设计了基于LMI的抗饱和补偿器。静态补偿器的设计,不仅没有增加系统固有阶数,还能保证系统在输入受限情况下的稳定。仿真结果表明,系统在输入受限情况下,抗饱和补偿器能够保证系统闭环稳定。
(18)
(19)
[1] Boyd S,Ghaoul L E, Feron E. Linear Matrix Inequalities in System and Control Theory[M]. Society for Industrial Mathematics, 1994.
[2] Miyamoto S,Vinnicombe G.Robust Control of Plants with Saturation Nonlinearity Based on Coprime Factor Representation[C].36thCDC.Kobe,Japan.1996:2838-2840.
[3] Mulder E,Kothare M,Morari M.Multivariable Anti-windup Controller Synthesis Using Linear Matrix Inequalities[J].Automatica,2001,37(9):1407-1416.
[4] Grimm G, Hatfield J, Postlethwaite I, Teel A, Turner M, Zaccarian L. Antiwindup for Stable Linear Systems with Input Saturation:An LMI-based Synthesis[J].IEEE Transactions on Automatic Control , 2003,48(9): 1509-1525.
[5] Hu T, Teel A, Zaccarian L.Nonlinear L2 Gain and Regional Analysis for Linear Systems with Anti-windup Compensation[C].American Control Conference,Portland (OR),USA.2005:3391-3396.
[6] Hu T,Teel A,Zaccarian L.Stability and Performance for Saturated Systems via Quadratic and Non-quadratic Lyapunov Functions[J].IEEE Transactions on Automatic Control , 2006,51(11): 1770-1786.
[7] Hu T,Teel A, Zaccarian L.Anti-windup Synthesis for Linear Control Systems with Input Saturation: Achieving Regional,Nonlinear Performance[J].Automatica, 2008,44: 512-519.
[8] Hencey B,Alleyne A.A Static Anti-Windup Compensator Design Technique for Robust Regional Pole Placement[C]. ASME International Mechanical Engineering Congress and Exposition Conference, 2006.
[9] Hencey B,Alleyne A.A KYP Lemma for LMI Regions[J].IEEE Transactions on Automatic Control, 2007, 52 (10): 1926-1930.
[10] Hencey B,Alleyne A.An Anti-Windup Technique for LMI Regions[J]. Automatica,2009,45: 2344-2349.
[11] Gomes da Silva J M,Jr.,Tarbouriech S.Anti-windup Design with Guaranteed Regions of Stability: An LMI-Based Approach[J].IEEE Transactions on Automatic Control, 2005, 50(1): 106-111.
The Anti-windup Compensator Design and Analysis for the Flexible Spacecraft Based on the LMI Method
WANG Mingzhao LIU Jinkun
Beihang University, School of Mechanical Engineering & Automation, Beijing 100191,China
Ananti-windupcompensatorbasedonthelinearmatrixinequalities(LMI)isdesignfortheinputsaturationincontrollingtheflexiblespacecraft.TheLQGcontrollercanguaranteethestabilityoftheclose-loopsystemintheidealconditionbutintheinputsaturationcondition.Therefore,thecompensatorbasedontheLMIisdesigned.Thecompensator,whichisstatewithoutincreasingthesystemorder,canguaranteeboththestabilityoftheclose-loopsystemandtheoptimalL2performanceofthesystem.Thesimulationresultsshowthatthecompensatorcanguaranteetheclose-loopstabilityandrobustnessnotonlyintheidealconditionbutalsointheinputsaturationcondition.
Inputsaturation; LMI;Anti-windup;Flexiblespacecraft;Compensator
*国家自然科学基金项目(61374048);高效博士点基金项目(20121102110008)
2013-06-08
王明钊(1989-),男,山东人,硕士,主要研究方向为航天器抗饱和控制等;刘金琨(1965-),男,辽宁人,教授,主要研究方向为滑模控制和自适应控制等。
TP273
A
1006-3242(2014)01-0063-05

