带旋转挠性太阳帆板卫星自适应控制

陆栋宁 刘一武

1. 北京控制工程研究所，北京 100190 2. 空间智能控制技术重点实验室，北京 100190



带旋转挠性太阳帆板卫星自适应控制

陆栋宁1,2刘一武1

1. 北京控制工程研究所，北京 100190 2. 空间智能控制技术重点实验室，北京 100190

为了应对航天器质量分布变化对姿态控制系统性能产生的影响，本文研究了带旋转挠性太阳帆板卫星的自适应姿态控制问题，其中对卫星本体转动惯量阵设计了参数自适应律，而惯量参数的不确定性是通过线性参数化方法表达的。基于类Lyapunov分析方法，这一时变系统的闭环稳定性和估计误差的有界性得到了证明。与PD控制的仿真对比表明，自适应控制对于卫星姿态和帆板驱动具有更好的性能。

对日定向太阳帆板；模态恒等式；自适应控制；参数估计

航天器的质量分布可能因为种种因素而发生很大变化，如燃料的消耗或意外泄漏，附件或内部元件的运动等等，这些因素将对姿控性能产生不利影响，而如果质量参数的变化过于激烈，甚至可能使系统失稳。为了应对这种情况，鲁棒控制和自适应控制是两类主要的解决方案。相比试图寻找不变的控制器以应对各种变化状况的鲁棒控制策略，自适应控制的基本思想是通过调节控制器来适应对象模型的变化，以较小的代价达到较高的系统性能。在航天器姿态自适应控制中，J. Ahmed 等人给出了适用于刚性航天器的自适应姿态跟踪控制律，其关键技巧是对星体转动惯量参数化以设计参数自适应律。通过周期指令对系统的激励，Ahmed 给出的自适应控制系统还能够辨识星体转动惯量[1]。此后，自适应控制技术被推广到了带有固定挠性附件的卫星姿态控制系统，并与其它一些先进控制策略巧妙地结合起来[2-3]，以获得更为优异的系统性能。

相比于具有固定挠性太阳帆板的卫星系统，本文研究了具有挠性旋转太阳帆板的卫星姿态跟踪问题，其中太阳帆板在驱动装置的作用下实现对日定向，使得电能获取效率最大化。由于太阳帆板的运动，系统动力学变得更复杂，此时航天器的转动惯量，以及航天器姿态运动与附件挠性振动之间的耦合系数阵都是连续时变的。一个早期的控制方案是针对某个特定太阳帆板位置，如45°下的卫星系统构型，设计鲁棒H∞控制器[4]。另外一些方法则是将系统动力学方程从本体坐标系投影到太阳帆板局部坐标系下，以实现多输入多输出耦合系统解耦为3个单输入单输出系统，在此基础上再设计LQG或H∞控制器[5]。直到近年来，伴随星载计算技术的进步，增益调度等自适应控制算法开始应用到这类复杂卫星之中[6]。

本文的主要目标是将自适应控制策略从附件固定的卫星系统推广到附件运动的系统中。与以往的结果不同的是，并不致力于针对由于太阳帆板转动引起的系统转动惯量阵变化设计自适应控制系统，因为通过对系统动力学的研究可以发现，太阳帆板旋转引起的转动惯量的变化是能够比较精确地计算出来的。而另一方面，如果考虑整个系统的参数变化问题，那么不可避免地要对挠性耦合系数阵的时变特性一起考虑，而挠性耦合系数阵规模巨大，这在目前的条件下设计自适应算法仍然存在困难。因此,转而致力于考虑航天器中心体转动惯量阵的不确定性，利用线性参数化技术设计了自适应姿态跟踪控制算法。利用类Lyapunov函数证明了闭环系统的稳定性，并讨论了惯量矩阵的估计误差。最后通过数值仿真，将本文的理论结果与经典PD控制进行对比，证实本文设计的控制器具有更好的性能。

1 数学模型

不失一般性，考虑如图1所示的具有单翼旋转挠性太阳帆板卫星模型。设ω= [ωxωyωz]T为卫星三轴姿态角速度，Ω为帆板转速，η=[η1η2…ηN]T为N阶挠性模态坐标，那么带有可控旋转挠性太阳帆板卫星动力学模型为[7]

(1)

(2)

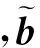
(3)

Cbs是向量从帆板固连坐标系到本体坐标系的坐标转换矩阵：

(4)

其中,α∈[0, 2π)是帆板沿俯仰轴的转角。Jbs是帆板转动对卫星姿态运动的刚性耦合系数阵，其表达式为

(5)

图1 带旋转挠性帆板卫星模型

与之相对，Hs和Hbs是挠性耦合系数阵，其中Hs是帆板振动对其自身转动的耦合系数阵，Hbs是帆板振动对卫星姿态运动的耦合系数阵，且

(6)

式中,Ps是帆板振动对其自身平动的耦合系数阵。显然，Hs和Ps是恒值矩阵，而Hbs和Jbs是周期时变矩阵，它们取决于帆板转角位置。这些矩阵具有如下一些重要性质，即

(7)

这些关系式称为模态恒等式[8-9]，它们在后续章节的控制器设计中具有重要作用。

具有受控帆板卫星的一个基本控制问题是卫星本体姿态对地定向，而帆板对日定向。定义本体姿态相对轨道坐标系的3个欧拉角为滚动角(ψ)，俯仰角(θ)，偏航角(φ)，那么在小角度假设下的姿态误差运动学方程可以表达为

(8)

其中Θ=[ψθφ]T,而

(9)

ωd=[0 -ωo0]T是期望的姿态角速度，而ωo是卫星轨道角速度。另一方面，帆板需对日定向，其跟踪误差方程为

(10)

式中，Δα=α-Ωdt且Ωd=ωo。因此，控制问题可以归结为:根据可测量输出Θ,ω,α和Ω设计自适应控制器T和τ使得

(11)

2 自适应控制系统设计

为了设计自适应控制器，设k1>0,k2>0并定义下述新变量

(12)

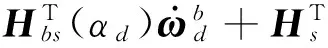
(13)

(14)

注意到J=Jb+Js，而Js和Jbs可由式(2)和(5)精确计算得到。假设本体转动惯量阵由于燃料消耗存在不确定性。为了对其进行估计，取

(15)

式中χ=[JbxxJbyyJbzzJbxyJbxzJbyz]T是本转动阵Jb的各分量，而算子

(16)

(17)

类似地，对于式(1)的第2个方程，有

TIs
τ-TIs

(18)

对于第3个方程，注意到式(13)可得

(19)

取k3>0，k4>0，考虑自适应控制器

(20)

其参数自适应律为

(21)

定理1 设中心刚体转动惯量阵缓慢变化或两次质量分布发生变化之间保持恒定。存在充分大ki>0 (i=1, … , 4)，自适应控制器(20)和(21)作用下的系统(1)、(8)和(10)是渐近稳定的，而对转动惯量阵Jb的估计误差有界。

证明 考虑如下类 Lyapunov 函数

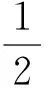
(22)

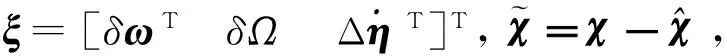
(23)

式中1是N×N单位阵。显然V的正定性取决于矩阵M。利用模态恒等式

(24)

其中,所有零矩阵都有适当的维数。那么，矩阵M的特征值就是本体转动惯量阵的特征值以及0, 1, …, 1, 且均为非负数。因此V≥ 0，即V有下确界。

考虑闭环系统(17)、(18)和(19)，对函数V求时间导数可得

(25)

(26)

其中,λm是阻尼阵D的最小特征值。存在如下不等式

(27)

其中ε>0,有

(28)

式中

(29)

(30)

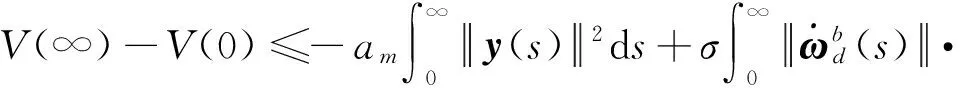
(31)

其中‖‖2是L2范数。因为V(t)≥0，进一步可以得到

(32)

(33)

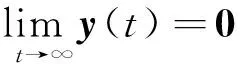
(34)

因此，由动力学关系可知，系统(1),(8)和(10)在自适应控制律(20)和(21)是渐近稳定的。但是，根据参数自适应律(21)，对本转动惯量阵Jb的估计伴随状态的收敛而收敛，但不一定是真值。因此其估计误差是有界的。证毕。

3 仿真研究

利用美国 GOES-8号气象卫星参数[7]，对自适应控制系统进行数值仿真，并与PD控制作对比。控制器增益设为k1=2，k2=0.5，k3=100，k4=80，参数估计增益矩阵为 Г = 5 × 105× 16×6，卫星姿态欧拉角以及帆板转角初值设为0。模态坐标初值设为 0.005×[1 1 1 1 1]T，而惯量估计初值为[1000 1000 1000 -10 -10 -20]Tkg·m2。其余状态变量初始值均为0。设本体主惯量在10s时发生大约20%的变化。

在上述条件下对闭环系统的自适应控制和 PD 控制利用 ode23 解算器进行了 25s仿真，其输入及输出响应如图2～7所示。仿真结果表明，两类控制器均达到了控制目标，且控制力矩都在合理范围内。由图6可知，转动惯量的自适应辨识在系统稳定后即停止，由于缺乏持续激励条件，并没有收敛到真值。但是相比 PD 控制，自适应控制下的状态变量经历更短的动态过程，姿态跟踪误差和振动抑制效果更好。

图2 卫星姿态欧拉角

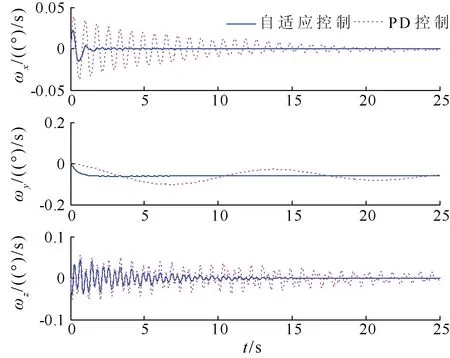
图3 卫星姿态角速度

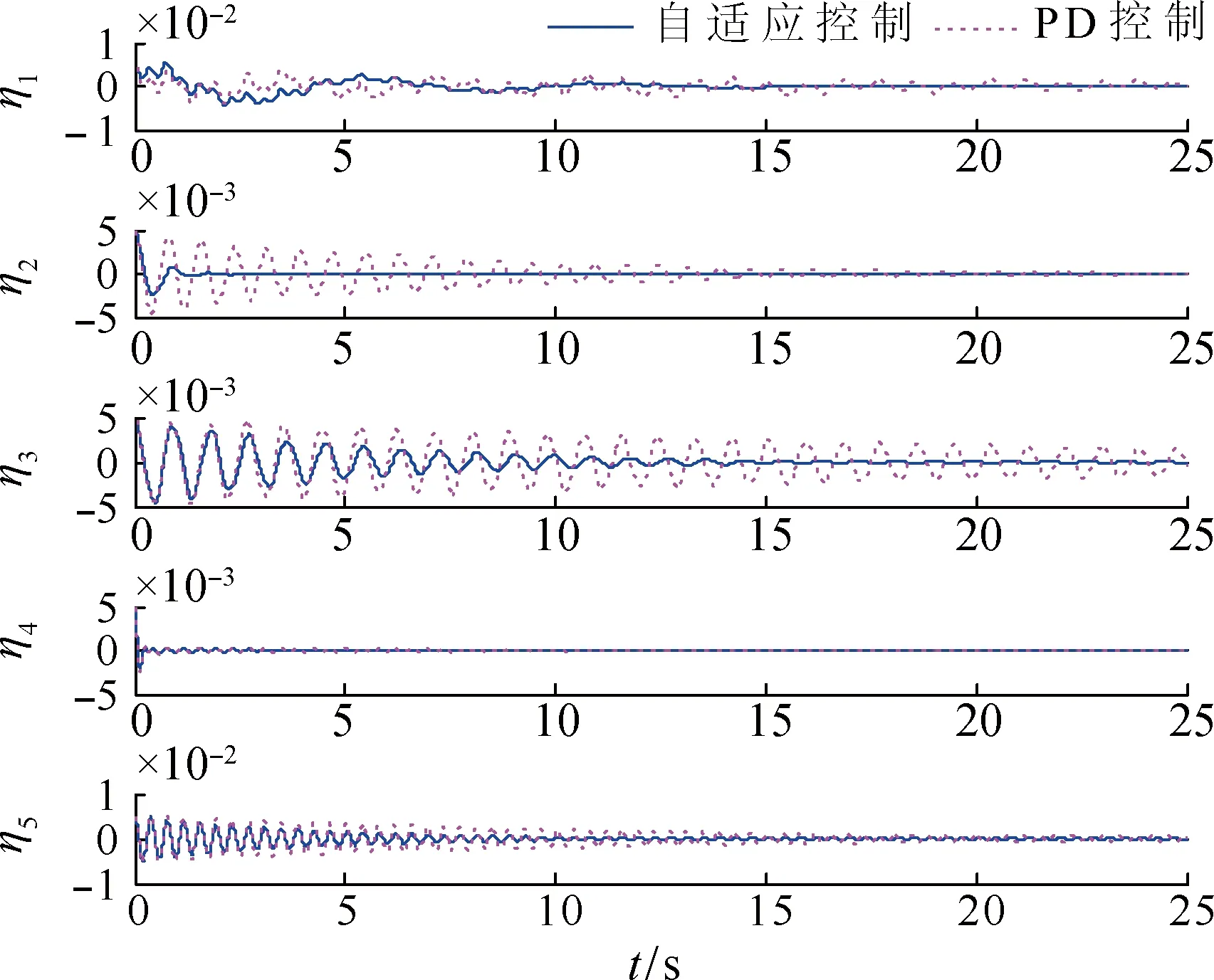
图4 帆板挠性振动模态坐标

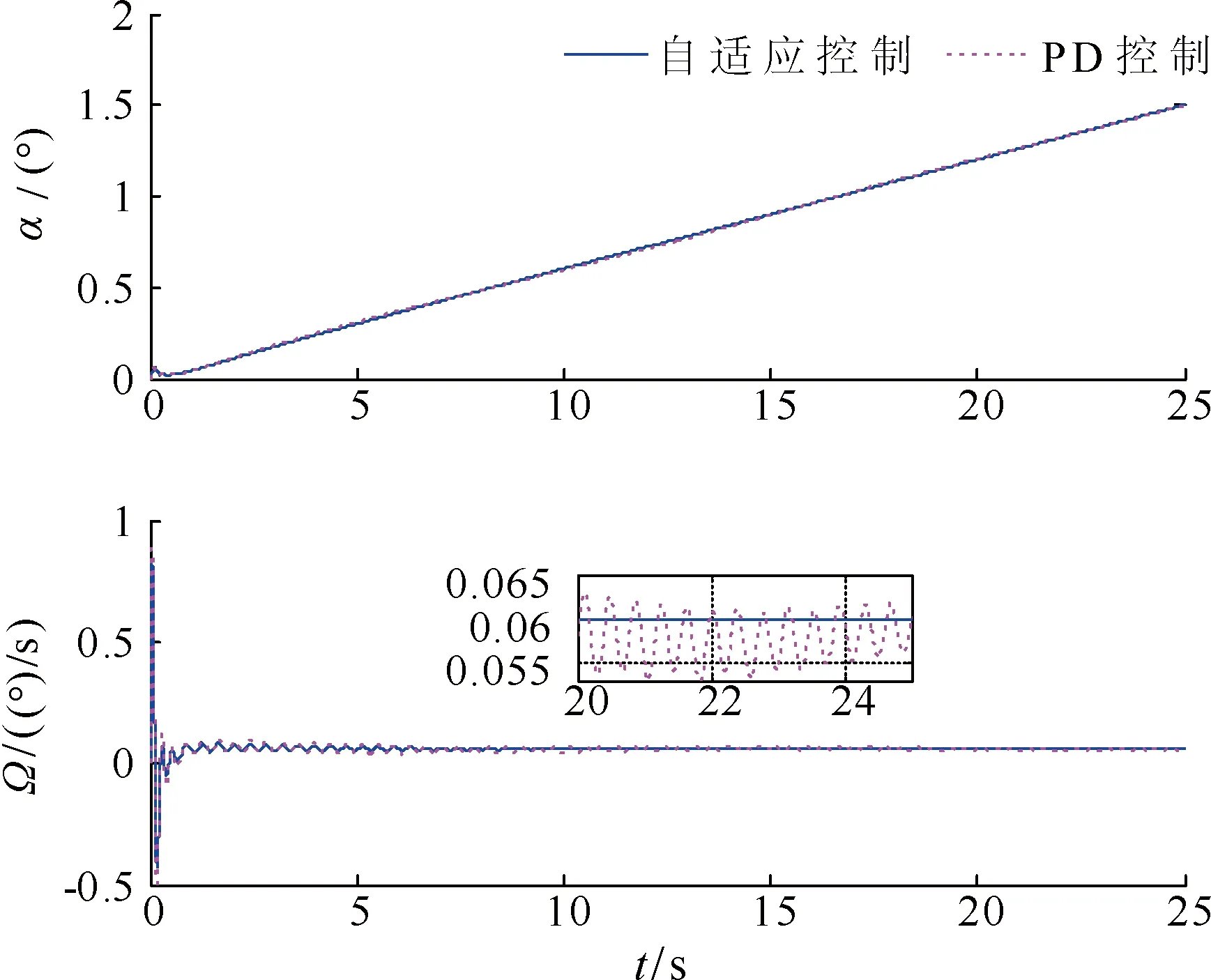
图5 帆板转速和转角

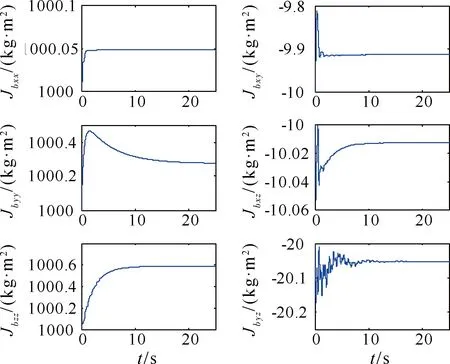
图6 卫星本体惯量参数估计

图7 姿态控制力矩和帆板转矩

4 结论

本文考虑了本体转动惯量阵在参数发生变化时的自适应控制问题，将线性参数化方法推广到了带有旋转挠性太阳帆板卫星的姿态控制中，基于 Lyapunov 理论对系统稳定性进行了数学证明，通过数值仿真验证了控制器的性能。但是，如果将这类参数化方法进一步推广到对整星质量参数作自适应控制时，由于需要辨识的参数过多，仍然存在很大困难，值得进一步研究。

[1] Ahmed J. Adaptive Asymptotic Tracking of Spacecraft Attitude Motion with Inertia Matrix Identification [J]. Journal of Guidance, Control, and Dynamics, 1998, 21(5): 684-691.

[2] 胡庆雷, 马广富, 姜野.控制受限的挠性航天器姿态机动自适应变结构输出反馈控制[J].宇航学报,2007, 28(4): 875-879. (Hu Q L, Ma G F, Jiang Y. Adaptive Variable Structure Output Feedback Maneuvering Control for Flexible Spacecraft with Input Constraints [J]. Journal of Astronautics, 2007, 28(4): 875-879.)

[3] 马广富, 周稼康, 胡庆雷, 等.卫星编队飞行输出反馈姿态协同跟踪控制[J].宇航学报, 2011, 32(10): 2133-2139. (Ma G F, Zhou J K, Hu Q L, et al. Output Feedback Attitude Synchronization Tracking Control for Formation Flying Satellite [J]. Journal of Astronautics, 2011, 32(10): 2133-2139. )

[4] Valentin-Charbonnel C, Duc G, Ballois S L. Low-order Robust Attitude Control of an Earth Observation Satellite [J]. Control Engineering Practice, 1999, 7: 493-506.

[5] Kida T, Yamaguchi I, Chida Y, et al. On-Orbit Robust Control Experiment of Flexible Spacecraft ETS-VI [J]. Journal of Guidance, Control, and Dynamics, 1997, 20(5): 865-872.

[6] Hamada Y, Ohtani T, Kida T, et al. Synthesis of A Linearly Interpolated Gain Scheduling Controller for Large Flexible Spacecraft ETS-VIII [J]. Control Engineering Practice, 2011, 19: 611-625.

[7] Tadikonda S S K. Articulated, Flexible Multibody Dynamics Modeling: Geostationary Operational Environmental Satellite-8 Case Study [J]. Journal of Guidance, Control, and Dynamics, 1997, 20(2): 276-283.

[8] Hughes P C, Skelton R E. Modal Truncation for Flexible Spacecraft [J]. Journal of Guidance and Control, 1981, 4(3): 291-297.

[9] Hablani H B. Modal Identities for Multibody Elastic Spacecraft [J]. Journal of Guidance, 1991,14(2): 294-303.

[10] Slotine J-J E, Li W. Applied Nonlinear Control [M]. Beijing, China Machine Press, 1991.

Adaptive Control of the Spacecraft with a Rotating Flexible Solar Array

LU Dongning1,2LIU Yiwu1

1. Beijing Institute of Control Engineering, Beijing 100190, China 2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China

Inordertoattenuatetheinfluencecausedbythevariationofthemassdistributionofsatellitestotheattitudecontrolsystem,thispaperisconcernedwiththeadaptiveattitudecontrolproblemofasatellitewitharotatingflexiblesolararray.Anadaptivecontrolschemeisdesignedtoadjustthevariationsofthemassdistributionsofthespacecraftcentralbody.Theuncertaininertiaparametersareisolatedbylinearparameterizationmethod.BasedontheLyapunov-likeanalysis,closed-loopstabilityandboundednessofidentificationerrorsofthistime-varyingsystemareensured.NumericalsimulationscomparedwithPDcontrolareperformedtoshowthattheadaptivecontrolforthespacecraftandthesolararrayhasbetterperformances.

Sun-trackingsolararray;Modalidentity;Adaptivecontrol；Parameterestimation

2013-03-12

陆栋宁(1982-),男，广东人，博士研究生，主要研究方向为复杂航天器姿态动力学与控制；刘一武(1968-)，男，湖南人，研究员，主要从事航天器导航、制导与控制研究。

TP316.2

A

1006-3242(2014)01-0049-06