捷联惯导系统初始对准可观测性分析
杨建锋
燎原无线电厂,成都610100
陀螺漂移和加速度计零偏都是随机的,因此捷联惯导系统是随机系统。初始对准误差是捷联惯导系统的主要误差来源之一。因此,在开始惯性导航之前,必须完成初始精对准,使导航初值误差最小。初始对准的本质是应用Kalman 滤波器将失准角和惯性仪表的随机误差作为状态量,通过最优估计的方法估计出来,达到消除失准角和随机误差的目的。实际上由于仪表误差和外界干扰的存在,上述误差是不能被完全补偿的。利用Kalman 滤波器进行初始精对准时,对可观测状态量,Kalman 滤波收敛可以估计出这些状态量,而对不可观测状态量,Kalman滤波器无法估计出来。秩相同的矩阵,Kalman 滤波器效果也不相同,这是由于状态量的可观测性不同。因此,研究系统状态量的可估计性,首先必须研究系统的可观测性。
文献[1]提出了利用Kalman 滤波协方差矩阵分析系统的可观测性,以协方差矩阵的特征值大小来衡量观测性的强弱。但是该方法只能在设计Kalman 滤波器时通过仿真来预估,不能直接通过系统的状态方程和观测方程来分析。文献[2]先用奇异值判别法与Кузовков 方法结合,确定不可观测状态量的选择,然后利用找出的3 种情况7 阶子系统,通过比较子系统奇异值的大小来确定最佳的可观测性组合。这种方法要求先对系统进行初步的分析,通过分析缩小不可观测状态量的范围,不能直接判断每个状态量的可观测性。本文应用奇异值分解理论证明了一个关于不完全可观测线性定常系统状态量判别的定理,应用定理直接分析了每个状态量的可观测性。
在SINS 初始对准设计过程中,应用Kalman 滤波器进行状态量的最优估计,系统不完全可观测,有3个状态量无法估计。为分析出不可观测的状态量,证明了一个可用于定量分析的定理,应用这个定理得出了SINS 初始对准最佳观测状态的组合。通过应用定理可以看出,该方法简单且直观。
1 初始对准误差方程
研究捷联惯导系统静基座初始对准问题,由于是静基座,因此所考虑的系统是线性定常系统,捷联惯导系统初始对准的误差模型为:
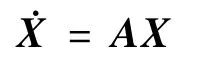
状态变量选择:
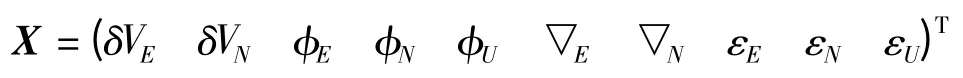
在上述模型中选用东北天(East -North -Up)坐标系为导航坐标系,δV 和φ 分别代表速度和姿态误差;▽和ε 分别代表加速度计零偏和陀螺漂移;式中,05×5和I5×5分别为指定维数的零矩阵和单位矩阵。
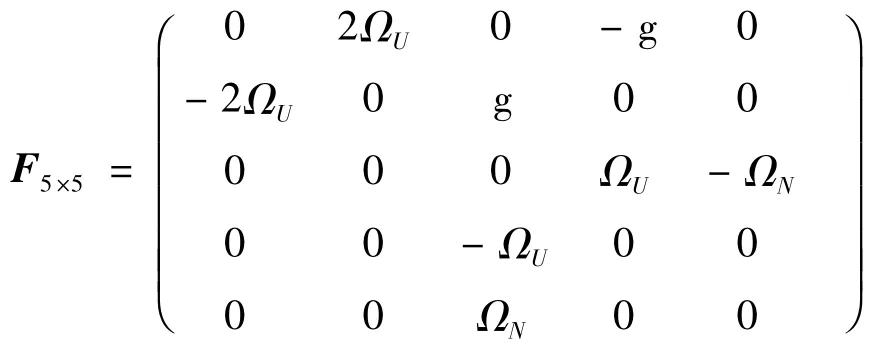
式中,ΩU= ωiesinβ,ΩN= ωiecosβ 为地球自转角速度在东北天坐标系下的2个分量,g = 9.8 m/s2和ωie= 7.292115 ×10-5rad/s 分别代表重力加速度和地球自转角速度,β 为惯导系统推算的地理纬度(取β = 45° ),惯导系统的Kalman 滤波模型为:

式中,W 为系统噪声阵,W = (wδVEwδVNwφEwφNwφU0 0 0 0 0)T,wδVE,wδVN,wφE,wφN和wφU均为零均值的高斯白噪声。
采用水平速度误差作为量测信号,则系统的观测方程为:
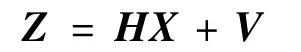
其中,Z = (ΔVEΔVN)T表示量测阵,观测噪声阵V =(V1V2)T为零均值的高斯白噪声过程,观测矩阵H = (I2×202×8)。
分析系统的可观测性矩阵:
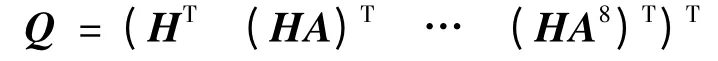
由于rankQ = 7 <10 ,因此系统不是完全可观测的,有3个状态量不可观测,但不知是哪3个状态量,下面首先证明一个定理,然后应用这个定理直接判断每个状态量的可观测性。
2 用奇异值判断状态量的可观测性
定 义 设A∈Cm×n,非负定阵AHA 的第i个特征值(i = 1,2,…,n)为λi(λi≥0 ),则称σi=为A 的奇异值。
引 理(矩阵的奇异值分解) 设A ∈Rm×n,则存在正交矩阵U ∈Rm×n和V ∈Rm×n,使得A =其中∑= diag(σ1,σ2,…,σr),对角元素按σ1≥σ2≥σ3…≥σr>0 顺序排列,而σi(i = 1,2,…,r)为矩阵A 的全部非零奇异值。
通过分析系统可观测阵的奇异值,可以得到系统的可观测性。奇异值越大,对状态量的估计精度越高;当系统的某个奇异值为0 时,估计问题就变成一个奇异问题,估计是无界的,状态量不能由测量值确定,系统状态量不可观测。并且根据奇异值的大小,可以判断状态量的可观测程度。奇异值越大,状态量的可观测性越好。
定 理 不完全可观测的线性定常系统,状态量为n个,可观测阵的秩为r(r <n),逐一判断状态量的可观测性:若去掉该状态量后的子系统可观测阵的秩仍为r,则该状态量不可观测;否则,该状态量可观测。
证明:先证命题的前半部分,反证,假设该状态量可以观测,由已知去掉该状态量的子系统可观测阵的秩仍为r,该子系统具有r个可观测的状态量,则由假设可知原系统具有r +1个可观测的状态量,这与可观测阵的秩为r 相矛盾,因此假设不成立。该命题的前半部分成立。
若去掉该状态量后的子系统可观测阵的秩不是r,则一定小于r,子系统不可观测的状态量数目又增加了,说明该去掉的状态量可以观测,证明命题后半部分成立。
综上所述,该命题成立。
矩阵秩的大小与所选精度eps有关,即当矩阵中元素小于精度时,可将其视为0。如果精度选择不当,秩就不能说明问题。在具体问题中,选取动态系统中最小元素的10-4倍作为标准,小于标准的数视为0。
系统可观测阵的秩和奇异值见表1,应用定理,可以得出系统不可观测的状态量为:▽E,▽N,εE,εN。
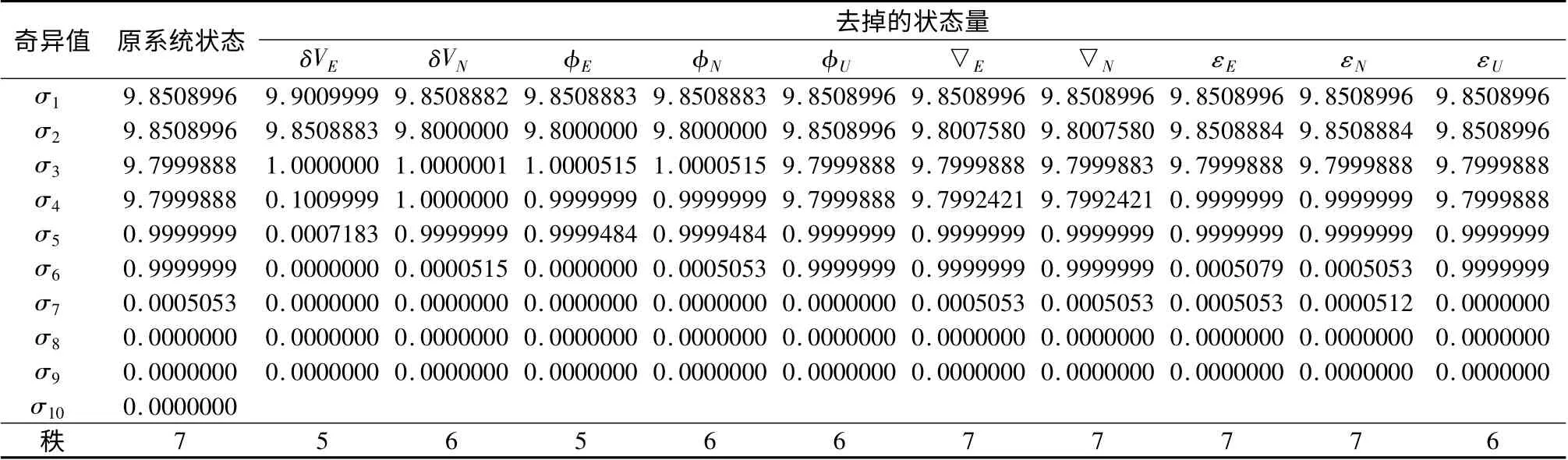
表1 系统可观测阵的秩和奇异值(eps =5 ×10 -8)
共有4个状态量不可观测,这4个不可观测的状态量与文献[3]得出的不可观测状态量是一致的。但这与判断的只有3个状态量不可观测相矛盾,说明这4个状态量可观测性不一样,即Kalman滤波器状态估计收敛程度和精度不一样。当出现不可观测的状态量个数大于根据原系统可观测阵得出的不可观测状态量个数时,可选取适当精度eps,结合系统可观测阵的秩与非零奇异值个数相等原理,应用定理,分析出可观测性较差的状态量,得出一组可观测性最佳的状态量组合,使得系统状态的可估计效果最好。
为比较出这4个状态量的可观测性,可以提高eps,由表1 中去掉的状态量奇异值栏中最后3个奇异值分析,εN的第7个奇异值比其它3个的第7个奇异值小1个数量级,因此选取eps为1 ×10-4,小于该数则将其视为0,结合系统可观测阵的秩与非零奇异值个数相等原理,由表1 中的数据可以判断出去掉εN的子系统,由秩为7 的子系统降为秩为6 的子系统。根据定理得出εN由不可观测状态量变为可观测状态量,只是可观测性较差。根据以上分析,由表1 中数据判断出系统有3个不可观测状态量,分别为▽E,▽N和εE。因此,当选取eps为1 ×10-4时,系统的可观测性最高,也即系统的可估计效果最好。通过分析,系统有3个状态量完全不可观测,有1个状态量的可观测性很差,近乎为不可观测。
应用该定理分析线性定常系统的可观测性时,设定一个适当的eps,可以直观和快捷判断出哪个状态量可以观测,哪个状态量不可以观测,而且适当选取eps,还可以比较不可观测状态量的可观测性,得出最佳的可观测状态量组合。
本文研究的可观测性分析方法适应性为:
1)对于线性时不变系统,由于它的系统方程和量测方程系数矩阵均为常数矩阵,因此可以适用;
2)对于线性时变系统的可观测性,可以先将时变系统分段定常化,建立分段式定常系统PWCS(Piece -Wise Constant System)模型,应用本文的方法来分析各状态量的可观测性;
3)在工程应用上,本文方法可应用于惯组标定工程实际问题,以及组合导航设计中的Kalman 滤波设计,通过系统方程和量测方程直接实现系统可观测性分析,无需进行Kalman 滤波运算,也不用进行仿真。
3 结论
针对传统奇异值分解理论定量分析系统可观测性需要结合其它理论的缺点,本文提出了使用奇异值分解理论直接分析系统的可观测性。证明了一个关于线性定常系统可观性判断的定理,应用这个定理定量分析了捷联惯导系统初始对准每个状态量的可观测性,该分析法简单、直观,可以对任意线性定常系统直接进行可观测性分析,而无需了解该系统的内部结构和关系。
[1]Ham F M,Brown R G. Observability,Eigen - values and Kalman Filtering[J]. IEEE Transaction on Aerospace and Electronic Systems ,1983,19(2):269 -273.
[2]王丹力,张洪钺.几种可观性分析方法及在惯导中的应用[J].北京航空航天大学学报,1999,25(3):342 -346.(Wang Danli,Zhang Hongyue. Methods for the Analysis of Observability and Their Application to INS Initial Alignment[J]. Journal of Beijing University of Aeronautics and Astronautics,1999,25(3):342-346.)
[3]万德钧,房建成.惯性导航系统初始对准[M]. 南京:东南大学出版社,1998.
[4]朱绍箕.姿态角传递对准研究[J].海军航空工程学院学报,2003,18(6):636-638.(Zhu Shaoji. Study on Attitude Transfer Alignment[J]. Journal of Naval Aeronautical Engineering Institute,2003,18(6):636-638.)
[5]库索夫可夫.控制系统的最优滤波和辨识方法[M].章燕申,译.北京:科学出版社,1984.
[6]Bar-Itzhack I Y,Berman N. Control Theoretic Approach to Inertial Navigation Systems[J]. Journal of Guidance and Control ,1988,11(3):237 -245.
[7]Jiang Y E and Lin Y P. Error Estimation of INS Ground Alignment through Observability Analysis[J]. IEEE Transaction on Aerospace and Electronic Systems ,1992,28(1):92 -97.
[8]付梦印,邓志红,闫莉萍. Kalman 滤波理论及其在导航系统中的应用[M].北京:科学出版社,2010.
[9]郑大钟.线性系统理论[M].北京:清华大学出版社,2002.
[10]程向红,万德钧,钟巡. 捷联惯导系统的可观测性和可观测性研究[J].东南大学学报,1997,27(6):6 -10.(Cheng Xianghong,Wan Dejun,Zhong Xun. Study on Observability and Its Degree of Strapdown Inertial Navigation System[J]. Journal of Southeast University,1997,27(6):6 -10.)
[11]程云鹏. 矩阵论[M]. 西安:西北工业大学出版社,2004.

