基于模糊控制器的热相移辅助超流体陀螺研究*

聂 威 赵 伟 郑 睿 刘建业

南京航空航天大学导航研究中心，南京 210016



基于模糊控制器的热相移辅助超流体陀螺研究*

聂 威 赵 伟 郑 睿 刘建业

南京航空航天大学导航研究中心，南京 210016

基于热相移辅助的超流体陀螺理论上的测量灵敏度能达到10-7rad/s，具有发展为高精度陀螺的潜力。但由于热相移注入过程中存在一定惯性，会使得超流体陀螺的测量精度急剧下降。为消除热相位注入惯性给系统带来的影响，本文提出了基于Fuzzy-PID的智能控制方案，该方案能针对大惯性产生的温度失调进行抑制，具有鲁棒性好、精确度高和不需要对对象精确建模等优点。本文根据该系统特性设计了超流体陀螺热相移模糊控制器，且通过仿真验证表明本文设计的Fuzzy-PID控制器有效减小了热相位注入惯性对超流体陀螺测量精度的影响。

超流体陀螺；模糊控制器；热相移

新型的超流体陀螺是当前惯性陀螺器件的重要研究方向，该陀螺的研究基础是基于波色爱因斯坦凝聚态理论形成的无粘性特殊物质—氦4流过弱连接时产生的交流约瑟夫森效应[1]。由于该原理在发展高精度陀螺方面具有巨大的发展潜力，因而引起了国内外研究者的极大关注，并且在该方面开展了卓有成效的工作[2-4]。目前已有研究者提出了基于幅值锁定的超流体陀螺的检测方案[5-7]，该方案在一定程度上扩展了系统测量量程，且在理论上可以实现10-7rad/s的灵敏度测量[6]。但目前通过对热相位注入方式进行的研究发现，该方式在补偿相位注入时存在惯性环节[8]，使得超流体陀螺测量输出的稳定性和解算精度严重下降，严重影响了超流体陀螺的高精度输出。

Fuzzy-PID的控制方法是一种智能控制方法，该方法不依赖于系统的精确数学模型，适用于非线性时变系统。而且该控制器在鲁棒性和适应性上也要优于PID控制器，能够很好的抑制大惯性产生的温度失调[9]。同时该控制器具有响应速度快，控制精度高等优点，适合复杂系统和高精度伺服系统的控制[10]。因此为解决热相移注入惯性导致的超流体陀螺测量稳定性和精度急剧下降问题，本文提出了基于Fuzzy-PID的超流体陀螺热相位注入控制方案，并进行了相应控制器设计和仿真验证。

1 基于热相移辅助的超流体陀螺工作原理

基于幅值锁定的角速度检测系统方案是通过加热反馈装置将系统当前的补偿量反馈到超流体环形腔内，以补偿外部转动引起的相位变化，从而使流体的幅值锁定在某一固定工作点[6]。该检测系统和超流体干涉仪的原理图如图1和2所示。

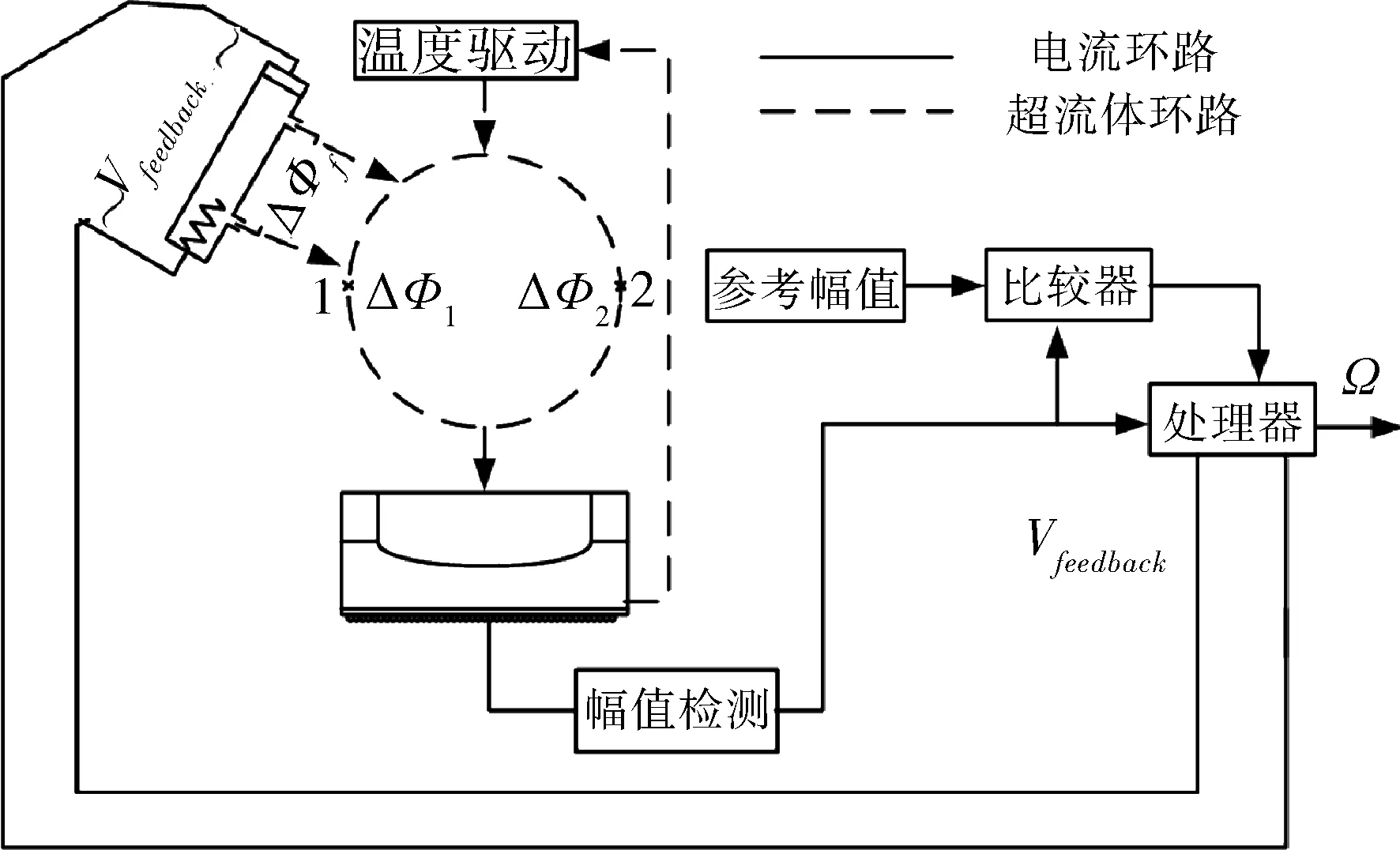
图1 幅值锁定原理图

图2 超流体干涉仪示意图

超流体陀螺的核心部分是基于交流约瑟夫逊效应的超流体干涉仪，超流体干涉仪主要包括2个对称布置的弱连接所形成的超流体环路，通过环路上方腔体内热源装置的加热，使得管内的超流体产生恒定的驱动势差Δμ，该势差使流过两弱连接的超流体分别产生Ic 1sin(Δφ1)和Ic2sin(Δφ2)的物质波，Δφ1和Δφ2分别为弱连接两端因热驱动产生的物质波相位。I(t)为此时管内超流体的总流量(kg/s)，表示为I(t)=Ic 1sin(Δφ1) +Ic2sin(Δφ1)[3]。为简化分析，假设两弱连接的特性是相同的，则此时有Ic0=Ic1=Ic2，故而管道里的总体流量为[11]

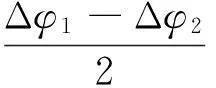
(1)

而外部旋转角速度Ω造成的弱连接的相位差为Δφrot=4πm4/h*Ω*A，考虑到注入的热相位Δφheat，则总的物质波相位差Δφ的表达式为[1]

Δφ=Δφ1-Δφ2=4πm4/h*Ω*A+Δφheat

(2)

对式dφ/dt=-Δμ/h[1]沿干涉环路积分得环路内总的物质波相位Δφ1+Δφ2=-4πΔμ*t/h[11]，由上述等式可得到环路内总的流体流量为

I(t)=2Ic0cos(Δφ)sin(-2πΔμ*t/h) (kg/s)

(3)

环路中超流体流量由上部薄膜位移所调制，因此利用高灵敏度的超导量子干涉仪实现对薄膜位移的测量，即可实现超流体流量的测量，如图2所示。

系统中热相位补偿锁定环节的结构如图3所示，管道内的物质波相移补偿主要由超流体部分特性变化产生。

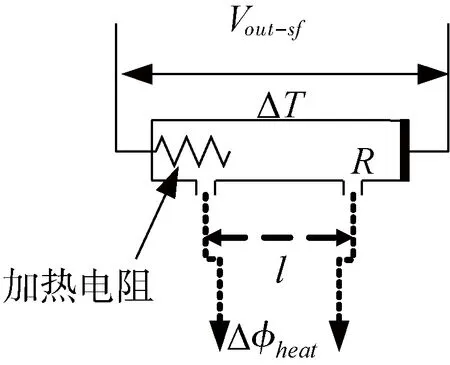
图3 相位补偿锁定环节示意图

在长度为l，半径为R的管道内，普通流体的流速vn与管路压力的变化量Δp的关系为vn=R2Δp/8ηl[12]，η为普通流体的粘度。管内的压力变化量Δp与管内温度变化ΔT的关系为Δp=kΔT[12]。对管道内的流体由质量守恒定律有vnρn=vsρs[12]，式中vs为超流体流速，ρs为超流体密度，ρn为普通流体密度。管路内超流体物质波的相位变化Δφ与vs的关系有Δφ=m4vs/h[1]，故注入的热相移与管内温度的关系可以表示为[12]：

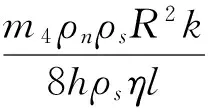
(4)

目前热相位的注入采用的是铜镍合金的加热电阻，文献[8]表明加热电阻的温升过程可以近似看作传递函数为1/(1+TQs)的惯性环节，惯性时间常数TQ为0.5ms。式(4)表明注入的热相位与管道内温升正相关，因此热相位的注入也存在惯性。

根据幅值锁定方案，若热相位的注入是实时注入，环路内因外界旋转造成的相位差与注入的热相位的和会实时保持在某一固定值。通过对实时注入的热相位进行测算即可测得外界旋转角速度。但是由于加热电阻的温升存在惯性环节，热相移不能实时注入，导致在采样时间内，流体的幅值不能锁定在预定的工作点，使得该采样时刻内超流体陀螺的解算误差产生剧变，这一过程会随着每次采样中对上次采样进行补偿而逐渐减小，直到温升稳定。同时对于整个超流体陀螺检测系统，热相移注入的惯性相当于给系统加入了一个闭环零点，而该闭环零点的加入减小了系统阻尼，加大了系统的输出振荡，降低了该检测系统的稳定性。因此，为减小热相移注入惯性给系统带来的不利影响，保证超流体陀螺能够实现稳定、连续高精度测量，本文针对无噪声影响的超流体陀螺模型设计了相应的控制器。

2 超流体陀螺模糊控制器设计

超流体环路中薄膜位移的变化与超流体流量的关系为[6]:

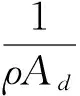
(5)

综合式(3)～(5)可以看出，该检测系统是包含了一阶惯性环节和积分环节的非线性时变系统。由于Fuzzy-PID复合型控制器具有不需要对受控系统进行精确的数学建模、灵活性高、广泛适用于复杂控制系统和高精度伺服系统等优点，因此对于超流体陀螺中的非线性时变系统的控制，本文采用Fuzzy-PID复合型控制器，旨在能使得超流体陀螺快速、准确地锁定在预定工作点。

根据超流体陀螺检测和工作的要求，以实时的薄膜位移偏离预定工作点的偏差量e和偏差变化率ec为输入量，以PID的参数Kp，Ki，Kd为输出量，设计二维Fuzzy-PID控制器。基于二维Fuzzy-PID控制器的超流体陀螺的结构如图4所示。

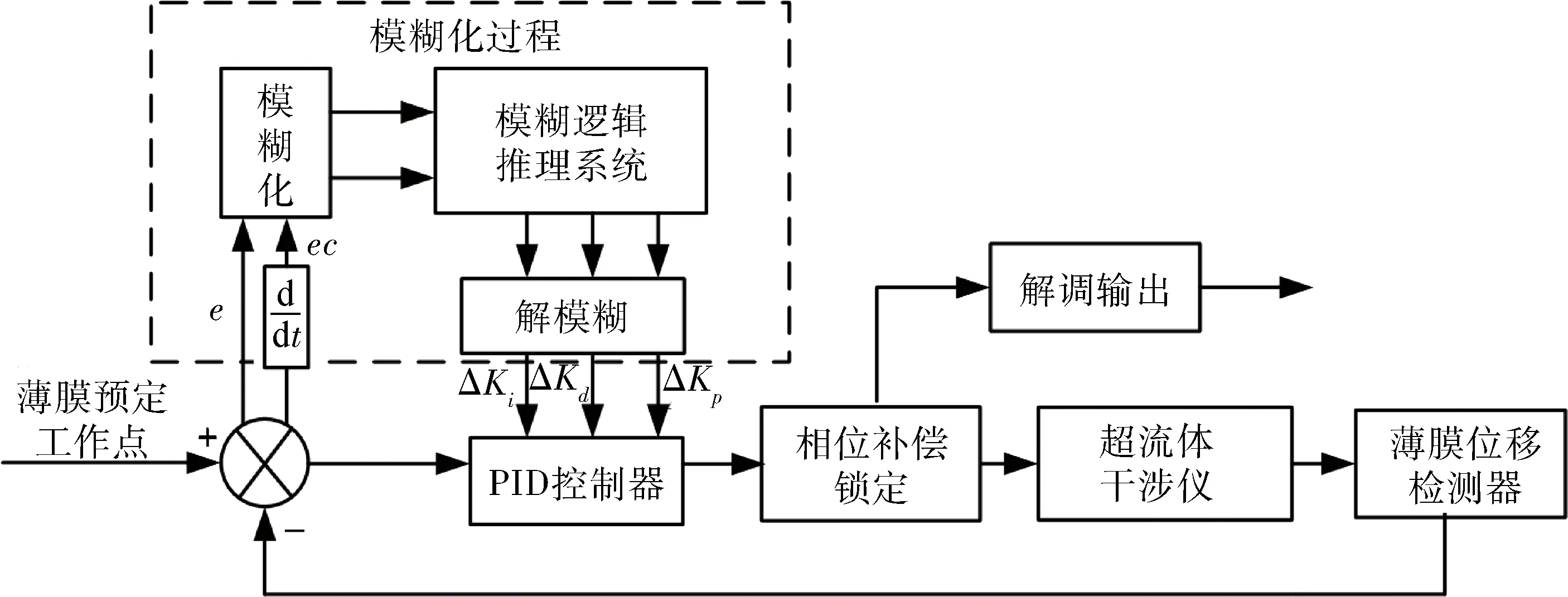
图4 带控制器的超流体陀螺结构示意图

通过Fuzzy-PID控制器的输出参数可以表示为[9]：

Kp=Kp′+ΔKp
Ki=Ki′+ΔKi
Kd=Kd′+ΔKd

(6)

式中，Kp′，Ki′，Kd′为预定的PID控制器参数，ΔKp，ΔKi，ΔKd为在线自整定参数。在线自整定参数是通过模糊控制器实现调整的，模糊控制器主要包括模糊化接口、知识库、解模糊化过程。在本控制器的设计中，首先通过仿真观察分析输入量的变化和变化率的范围，各变量的模糊子集为：e，ec={NB，NM，NS，N0，Z0，PS，PM，PB}，Kp={Z0，PS，PM，PB}，Ki={Z0，PS，PM，PB}，Kd={Z0，PS，PM，PB}。选取本控制器中的e的模糊论域为{-7 3}，量化因子为108；ec的模糊论域为{-3 3}，量化因子为103；Kp，Ki，Kd的模糊域分别为：{0 5}，{0 2}，{0 0.001}。量化因子分别为：10，10，2.5；各变量的隶属度函数均服从三角隶度函数分布。

由于3个参数对输出特性的影响不一样，比例增益的增加有利于减小系统偏差，但是过大的比例增益又会造成系统的不稳定；积分增益的主要作用是用来消除系统的静态偏差，提高系统精度，改善系统静态特性；微分增益的主要作用是用来控制被调量的振荡，减小超调量，减小调节时间，用来改善系统的动态特性。因此，模糊控制规则设计如下：

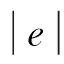
通过上述的分析和一些经验的总结，可以得到Kp，Ki，Kd的初始模糊整定表如表1所示。

3 仿真结果和分析

为验证本文设计的Fuzzy-PID控制器对超流体陀螺性能上的改善，利用MATLAB仿真工具对本系统进行仿真分析，仿真过程中主要的陀螺结构和运行参数均参考国外基于双弱连接的超流体干涉仪的实验数据[13]，角速度输入分别选择Ω=0.01sin(2π*10t)(单位：rad/s)和Ω=0.8t(单位：rad/s)，仿真时间0.1s，采样时间间隔为10-5s，热相位注入的惯性时间常数为0.5ms[8]。

通过设计好的模糊器结构和建立的模糊控制规则，建立一个完整的模糊PID控制器，其在MATLAB环境下的simulink图如图5所示。

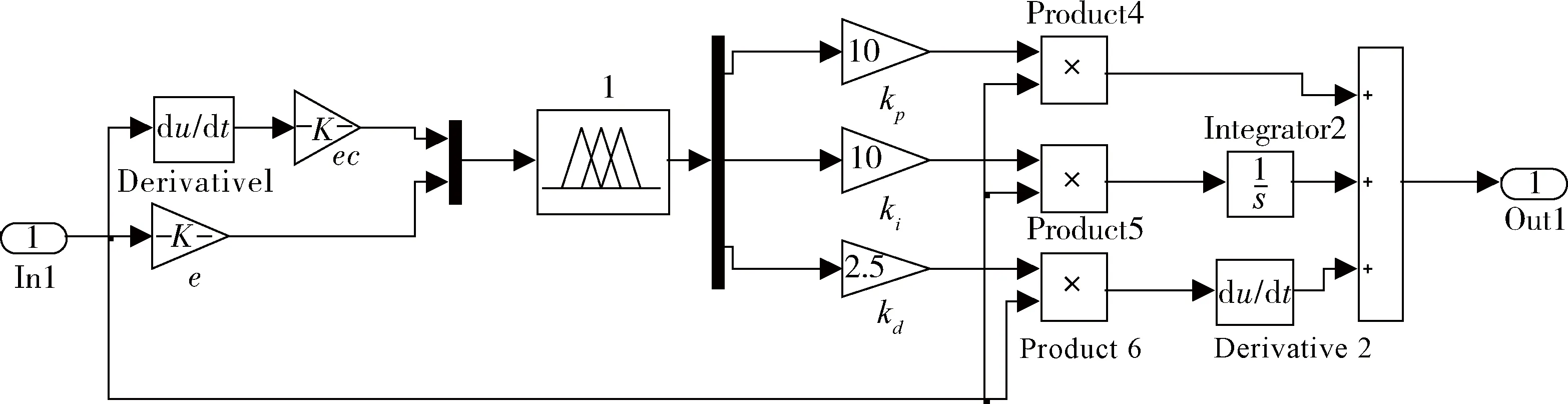
图5 模糊控制器的simulink图

由于热相位注入的惯性使得超流体幅值不能实时锁定在预定工作点，影响了基于幅值锁定的超流体陀螺性能，为验证Fuzzy-PID控制器对超流体幅值工作点的改善效果和调整Fuzzy-PID控制器，首先对超流体陀螺幅值变化进行仿真，仿真结果如图6和7所示。

图6 变角加速度输入下薄膜位移偏离工作点的位移曲线

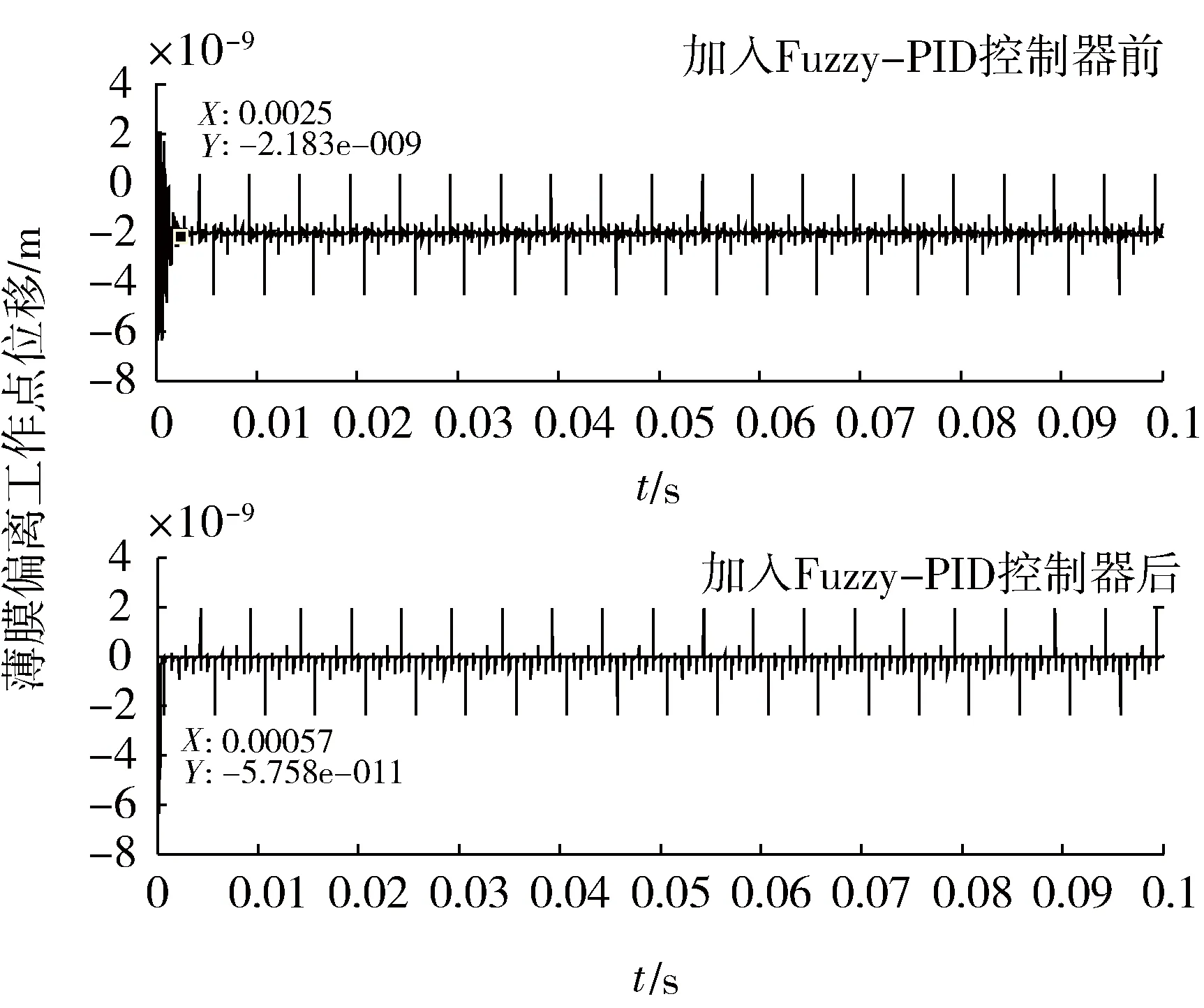
图7 恒定角加速度输入下薄膜位移偏离工作点的位移曲线

通过图6和7的仿真结果可以看出，无论是恒定角加速度输入还是变角加速度输入，加入Fuzzy-PID控制器后，超流体陀螺中流体幅值锁定在工作点的速度加快了，而且薄膜位移偏离预定工作点的稳态偏差值也降低了40倍左右。图6和7中曲线的毛刺主要是由于采用幅值锁定技术中因积分近似造成的偏值误差[6]，此处可以忽略不计。

在仿真验证Fuzzy-PID控制器对超流体幅值锁定工作点改善的基础上，为进一步研究该控制器对超流体陀螺性能的具体影响，本文针对加入Fuzzy-PID控制器后的系统解算误差进行了进一步的仿真，仿真结果如图8和9所示。

通过图8和9可以看出，加入Fuzzy-PID后，对于变角加速度的输入，超流体陀螺的解算误差收敛时间由加入控制器前的1.53×10-3s缩短到加入控制器后的2.4×10-4s，角速度解算误差稳态值也由加入控制器前的约10-4数量级降低到10-7。对于恒定角加速度的输入，超流体陀螺的解算误差收敛时间由加入控制器前的1.52×10-3s缩短到加入控制器后的3.1×10-4s，并且加入控制器后的角速度解算误差稳态值比加入控制器前的误差降低了近103倍。

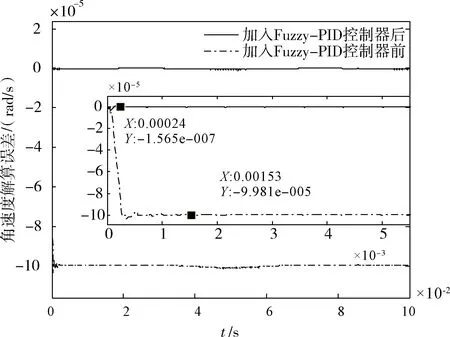
图8 变角加速度输入的解算误差曲线

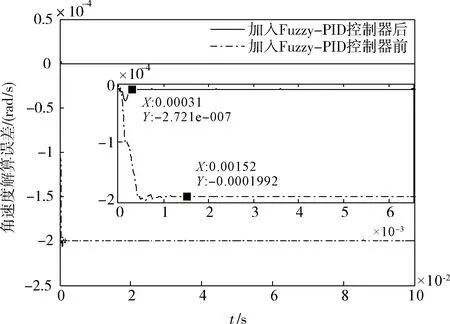
图9 恒定角加速度输入的解算误差曲线

综上可知，针对热相移注入惯性引起的超流体陀螺精度的下降，Fuzzy-PID控制器的加入有效改善了基于热相移辅助的超流体陀螺的稳态误差和响应时间，提高了超流体陀螺的测量精度。

4 总结

在基于热相移辅助的超流体陀螺测量方案基础上，本文研究了超流体陀螺原理和热相移的注入方式存在的惯性环节导致超流体陀螺的测量精度急剧下降的问题，针对超流体陀螺的非线性时变特性，提出了基于Fuzzy-PID的控制方案，采用该方案对超流体陀螺检测环路的控制器进行了设计仿真验证，结果表明Fuzzy-PID控制器有效改善了热相位注入惯性对超流体陀螺解算误差的影响，提高了超流体陀螺的测量精度。但本文未考虑相关噪声的影响，噪声对本系统的影响还待进一步的研究。

[1] Hoskinson E, Sato Y, Packard R. Superfluid 4He Interferometer Operating Near 2K[J]. Physical Review B, 2006,74(10):100509.1-100509.8.

[2] 谢征，等.双弱连接结构的高精度超流体陀螺的量程分析[J].中国惯性技术学报, 2011,19(1): 79-83.(XIE Zheng, et al. Analysis and Simulation of Measure Range of Souble Weak-links Structured High Sensitivity Superfluid Gyroscope[J]. Journal of Chinese Inertial Technology, 2011,19(1): 79-83.)

[3] Sato Y, Packard R.Superfluid Helium Quantum Interference Devices: Physics and Applications[J]. Reports on Progress in Physics, 2012, 75(1): 016401.

[4] Yuki, Sato And Richard Packard. Superfluid Helium Quantum Interference Devices: Present Status and Future Prospects[J]. Journal of Physics: Conference Series, 2012, 400(5): 052030.

[5] Sato Y, Joshi A, Packard R. Flux Locking a Superfluid Interferometer[J].Applied Physics Letters, 2007(074107):1-3.

[6] 冯铭瑜,等.双弱连接超流体陀螺信息提取与量程扩展技术[J].现代电子技术, 2012，35(2): 94-99.(FENG Ming-yu,et al.Information Extraction and Range Expanding Technology of Double Weak-link Structured Superfluid Gyroscope[J].Modern Electronics Technique, 2012，35(2): 94-99.)

[7] Narayana S, Sato Y. Compact Miniature High-Resolution Thermometer, Applied Superconductivity[J].IEEE Transactions on, On page(s): 2402-2405, Volume: 20, Issue: 6, Dec. 2010.

[8] 谢征.基于物质波干涉效应的新型低温超流体陀螺关键技术研究[D].南京:南京航空航天大学，2012:117-119.(XIE Zheng.Research on the Key Technology for New Cryogenic Superfluid Gyroscope Based on Matter Wave Interference Effect[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2012:117-119.)

[9] 屈毅，等.基于模糊PID控制的温室控制系统[J].计算机应用, 2009,29(7): 1996-1999.(QU Yi, et al .Greenhouse Control System Based on Fuzzy PID Control[J]. Journal of Computer Application, 2009,29(7): 1996-1999.)

[10] 冯斌,龚国芳,杨华勇.大流量液压系统的油温控制[J].浙江大学学报(工学版), 2011,45(4): 741-746.(FENG Bin，GONG Guofang，YANG Huayong.Oil Temperature Control of Large Hydraulic System[J].Journal of Zhejiang University, 2011,45(4): 741-746.)

[11] Packard R E, Vitale S. Principles of Superfluid-helium Gyroscopes[J].Physical Review B, 1992, 46(6): 3540-3549.

[12] Landau L D and Lifahitz E M.Fluid Mechanics [M]. Pergamon Press,1959:507-508.

[13] 冯铭瑜.基于双弱连接结构的超流体陀螺关键技术研究[D].南京:南京航空航天大学,2012.(Feng Mingyu.The Simulation Research on the Superfluid Gyroscope Effect Based on Double Weak-Links Structure[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2012.)

Research on Superfluid Gyroscope Aided by Heat Phase Shift Based on Fuzzy-PID

NIE Wei ZHAO Wei ZHENG Rui LIU Jianye

Navigation Research Center, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China

Theaccuracyofsuperfluidgyroscopeaidedbyheatphaseshiftcanbereached10-7rad/s,whichhasthepotentialofdevelopinghigh-precisiongyro.Buttheinertiaexistedintheheatphaseshiftinjectionprocessleadstotheaccuracyofsuperfluidgyroscopedramaticallyreduced.Inthispaper,anintelligentcontrolschemeknownasFuzzy-PIDisappliedtoeliminatetheinfluencewhichbroughtbyheatphaseshiftinjectionprocess.Themethodcaninhibittheoffsetoftemperatureforlargeinertiaandhasmanyadvantages,suchasgoodrobustness,highprecisionandneedlessprecisemodeling.TheproposedcontrollerbasedonFuzzy-PIDinthispaperisdesigned.Thesimulationshowsthatthecontrollercanreducetheimpactonmeasureaccuracyofsuperfluid-gyrowhichresultsfromtheprocessoftheheatphaseshiftinjectioneffectively.

Superfluidgyroscope; Fuzzy-PID；Heatphaseshift

*国家自然科学基金(61074162)；教育部博士点基金(200802870011)

2013-04-22

聂 威(1990-),男，湖北人，硕士研究生，主要从事新型陀螺技术研究；赵 伟(1971-)，男，山东人，博士，副教授，主要从事惯性技术、卫星定位和组合导航系统研究；郑 睿(1980-)，男，安徽人，博士研究生，讲师，主要从事惯性技术和新型惯性传感器研究；刘建业(1957-)，男，浙江人，教授，博士研究生导师，主要从事惯性技术、卫星定位和组合导航系统研究。

V241.5;U666.1

A

1006-3242(2014)01-0021-05