变后掠翼制导炸弹滑翔弹道优化设计*

赵 日 孙瑞胜 沈坚平

1.南京理工大学能源与动力工程学院，南京 210094 2.中国人民解放军95856部队，南京210028



变后掠翼制导炸弹滑翔弹道优化设计*

赵 日1孙瑞胜1沈坚平2

1.南京理工大学能源与动力工程学院，南京 210094 2.中国人民解放军95856部队，南京210028

为了探究影响变后掠翼制导炸弹滑翔增程能力的主要因素，采用粒子群优化算法分别对亚、跨、超三种投放条件下的滑翔弹道进行优化设计。固定外形与变后掠外形的优化对比结果表明：在超音速投放条件下采用变后掠翼外形具有明显增程效果，在亚音速投放条件下采用变后掠翼外形增程效果不明显。研究结果可为变后掠翼制导炸弹的总体设计提供参考。

制导炸弹；弹道优化；变后掠翼；粒子群算法

国外航空兵器的发展以及近年来的多场局部战争都已表明，制导炸弹正日益凸显其重要作用。变后掠翼制导炸弹作为制导炸弹中新的一员，相比固定翼制导炸弹具有射程远、机动突防能力强、毁伤效果好等许多优势[1]。早在1987年NASA就针对变后掠翼飞行器在亚跨音速下的气动特性进行了分析，得到了升阻特性随机翼后掠角的变化规律[2]。在此基础上，文献[3]将最优控制理论与粒子群算法相结合，分析了变后掠翼制导炸弹相对固定翼制导炸弹的滑翔增程能力。但目前还没有针对变后掠翼制导炸弹滑翔增程能力与投放条件之间关系的研究。为此，本文利用一种改进的粒子群算法得到了不同投放条件下变后掠翼制导炸弹的最优控制规律，并分析了变后掠翼制导炸弹在不同投放条件下的滑翔增程能力。

1 设计方案

对于变后掠翼制导炸弹而言，其滑翔增程能力不仅与攻角α(t)的变化规律有关，还与后掠角χ(t)的变化规律密切相关，这是因为后掠角的变化显著改变了制导炸弹的气动特性，从而影响到其飞行控制性能。因此为了获得变后掠翼制导炸弹的最优滑翔控制规律，可设计变外形方案为：后掠角χ(t)、攻角α(t)均作为待设计的控制变量，采用改进的粒子群算法进行优化。

对于固定翼外形制导炸弹，其滑翔增程能力由攻角α(t)的变化规律决定。作为对比可设计固定外形方案为：后掠角χ(t)=35°、攻角α(t)作为待设计的控制变量，采用改进的粒子群算法进行优化。

2 粒子群(PSO)算法

粒子群算法(PSO)是一种基于迭代的进化优化算法，易于实现且精度高，克服了局部寻优方法优化结果对初值敏感的缺陷问题，可实现全局寻优。

标准的PSO方程[4]如下：

(1)

其中，pin为粒子历史最好位置，xin为粒子当前位置，pgn为种群历史最好位置；vin为粒子在解空间中的飞行速度；c1，c2分别为社会系数和认知系数；r1n，r2n为[0,1]之间的随机数；W是惯性权重因子。

已有理论研究表明，基本的PSO算法不是一种全局优化算法[5]。为了获得全局最优解并使算法具有较好的收敛性，本文采用具有线性递减惯性权重的PSO算法[6]。

由于PSO算法属于直接法中的参数优化方法。因此，在应用时需要将控制规律参数化。通常控制变量的变化规律被设计成分段的线性函数形式或者指数函数形式，该形式的控制规律参数较少且结构简单[7]。控制变量的离散方法如下：

1)引入参数T=tf-t0；令τ=t/T，τ∈[0,1],并且将无因次时间区间m等分，得到m+1个节点；

2)引入参数向量ui，使控制变量u参数化，其中i=0,...,m；

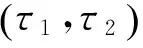
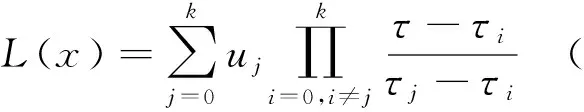
(2)

3 优化模型

3.1 弹道模型

为简单起见，本文采用制导炸弹在纵向平面内的质点弹道方程作为优化的弹道模型。方程形式为：

(3)

式中，θ为弹道倾角；X，Y为制导炸弹的阻力和升力，它们与动压q、参考面积S以及气动力系数Cx，Cy有关；而Cx，Cy则是攻角α、后掠角χ及马赫数Ma的函数；ε1(α,χ)=0,ε2(α,χ)=0为攻角和后掠角的控制方程。

3.2 约束条件

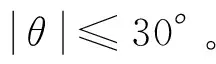
(4)

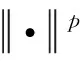
3.3 目标函数

滑翔段弹道优化的首要目标是使制导炸弹的射程最大化，同时还要满足各种姿态角的约束，因此可得综合目标函数为：

maxfu(x)=x(tf)-Pλ(x)

(5)

3.4 算法流程

结合上述模型构建方法及控制变量离散化方法，整个弹道优化迭代算法的基本流程[9]如下：

1)初始化模型：将弹道参数、粒子群算法参数等初始化；

2)根据式(1)更新粒子速度、位置信息；

3)根据式(2)生成一元三点不等距插值曲线，作为控制量；

4)代入控制量，解算弹道模型式(3)；

5)计算综合目标函数式(5)，调整个体最优适应度和种群最优适应度；

6)如果满足终止条件，则停止计算，输出最优个体位置及最优适应度；否则，返回步骤3)继续迭代。

4 仿真算例

以某变后掠翼制导炸弹为例进行优化设计，初始投放高度y0=12km，初始马赫数分别为Ma0=0.6，1.2，2.0，初始弹道倾角θ0=-arctan(4/V0)，结束高度yf=4km。本文计算时所取粒子群算法参数为：方案1的粒子维数为21，方案2的粒子维数为41；每次迭代过程中的粒子个数即种群规模N=100，社会系数和认知系数c1=c2=1.8，惯性权重由1.0线性递减到0.4，最大迭代次数为100次。

图1～4为不同优化方案时的滑翔段弹道对比曲线；图5和6为各方案弹道阻力、升力对比曲线。表1为各个条件下不同方案弹道优化结果。图表中方案1表示固定外形方案，方案2表示变后掠外形方案。

由优化结果分析可知：1)在亚、跨声速条件投放时，2种优化方案的射程差别不大。且由图3可知,在亚声速投放时方案2优化出的结果即为全展开状态χ(t)=35°，这可作为一个特例，说明在亚声速投放条件下变后掠翼外形增程效果不明显；2)在超声速投放时，变后掠翼方案的射程比固定外形制导炸弹的射程增加17km，增程效果明显。且由图5和6可知，超音速投放时，采用变后掠翼方案的阻力在初始阶段较固定外形方案明显要小，而升力却有较为显著的增加，这可以从物理意义上解释变后掠翼制导炸弹射程较远的原因；3)在变后掠翼弹道优化中，制导炸弹的后掠角大多在35°～55°之间变化，说明小后掠角时气动增程性能较优。

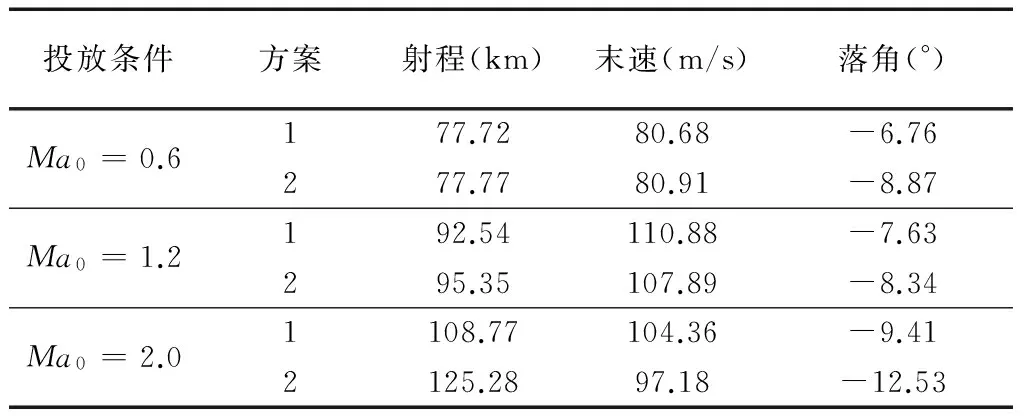
表1 各个投放条件下末端指标比较

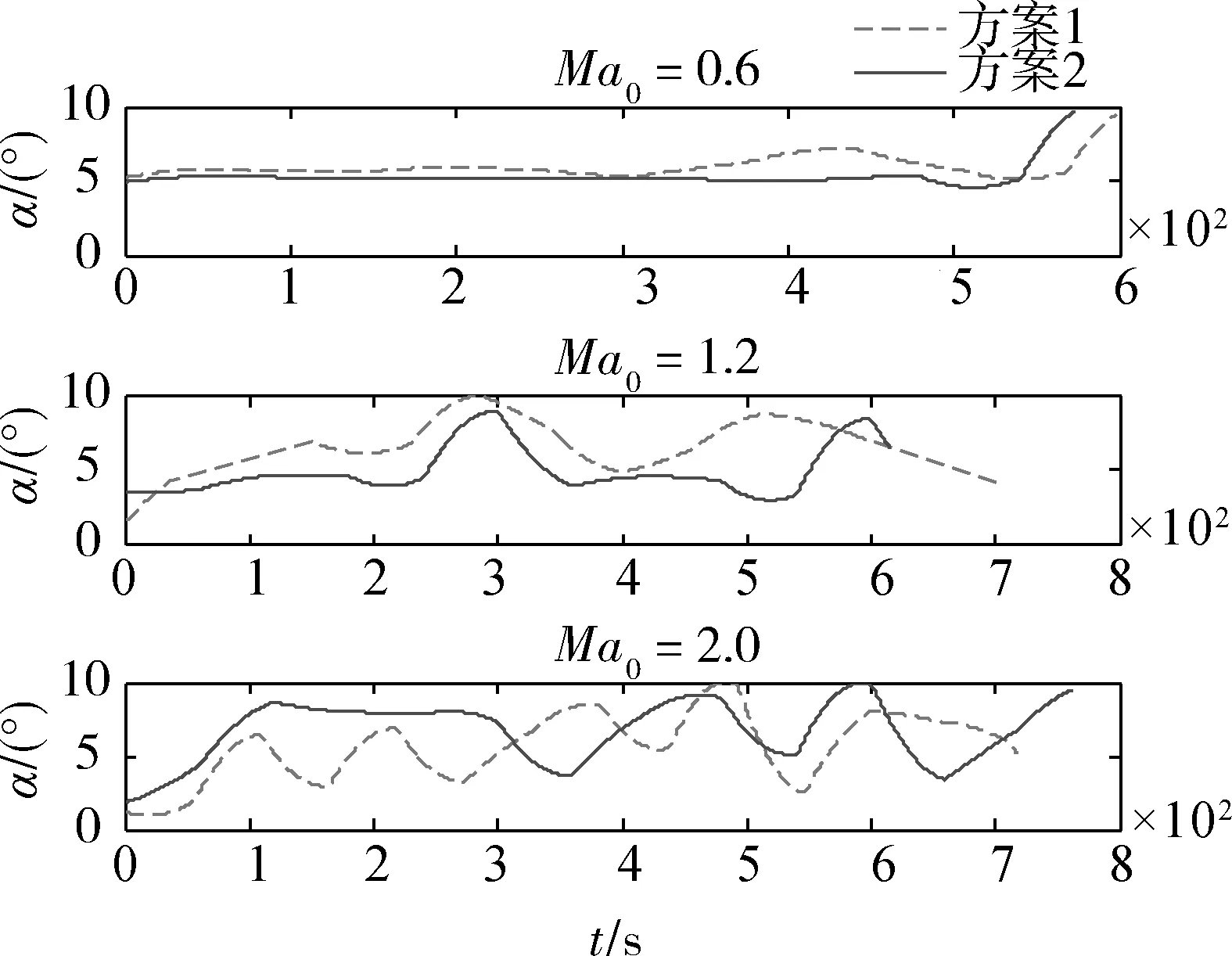
图2 攻角变化曲线

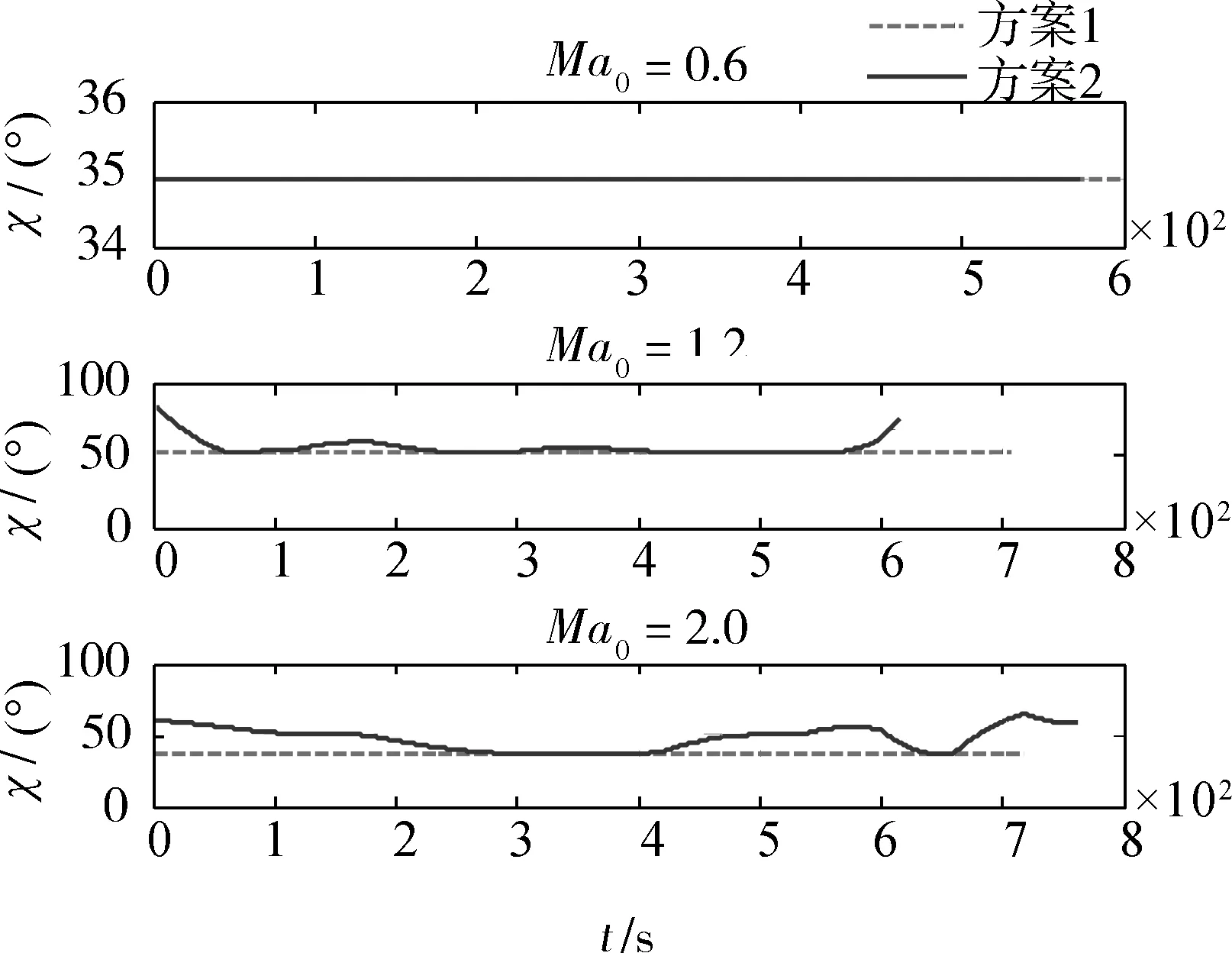
图3 后掠角变化曲线

图4 飞行速度变化曲线

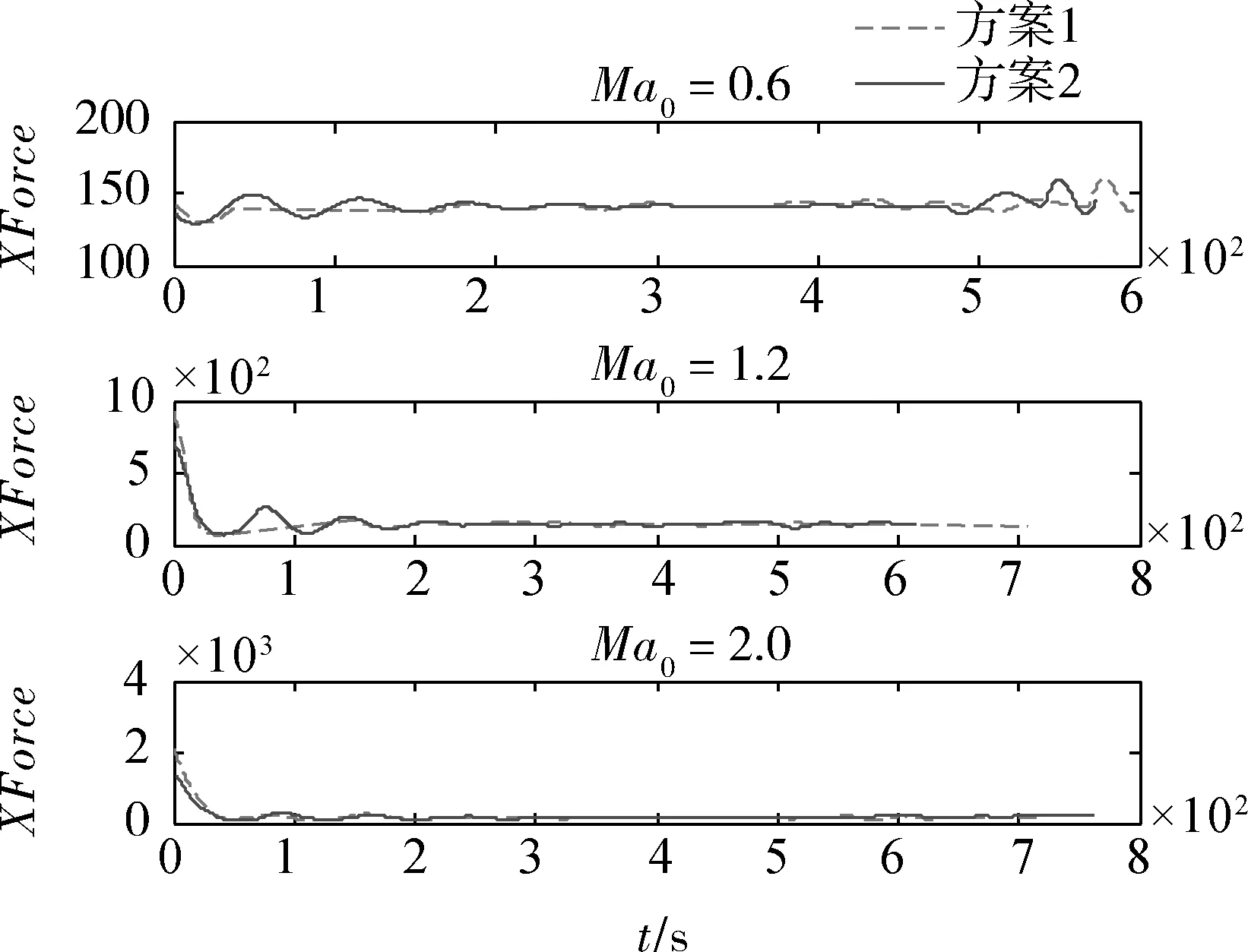
图5 阻力变化曲线

图6 升力变化曲线

5 结束语

针对某机载变后掠翼制导炸弹滑翔段弹道进行研究，结合粒子群优化算法进行弹道优化，分析了变后掠翼制导炸弹在不同投放速度下的滑翔增程能力，给出了后掠角及攻角控制量在滑翔段的控制规律，通过仿真对比说明了变后掠翼制导炸弹在超音速投放时具有良好的增程效果，结果可为变后掠翼制导炸弹的弹道设计及作战使用提供参考。

[1] T Takahashi，R J Spall，D C Turner, et al. A Multi-disciplinary Assessment of Morphing Aircraft Technology Applied to Tactical Cruise Missile Configurations[R]. AIAA，2004-1725.

[2] F Manie, C Rehbach. Study of a Variable Sweep Wing in Sub or Transonic Flow[R].NASA Technical Translation.

[3] 李伟明，孙瑞胜，吴军基，刘鹏云.变后掠翼航弹滑翔弹道优化设计[J].弹道学报，2012，42(2):6-10. (Li Weiming，Sun Ruisheng，Wu Junji，Liu Pengyun. Optimization of Glide Trajectory for Aerial Bomb with Morphing Swept Wings[J].Journal of Ballistics，2012，42(2): 6-10.)

[4] 崔志华，曾建潮.微粒群优化算法[M].北京:科学出版社，2011.(Cui Zhihua，Zeng Jianchao. Particle Swarm Optimization[M].Beijing:China Social Science Press，2011.)

[5] 张慧斌，王鸿斌，胡志军.PSO算法全局收敛性分析[J].计算机工程与应用，2011，47(34):61-63.(Zhang Huibing，Wang Hongbin，Hu Zhijun. Analysis of Particle Swarm Optimization Algorithm Global Convergence Method[J]. Computer Engineering and Applications，2011，47(34):61-63.)

[6] 姚灿中，杨建梅.基于变惯性权重及动态邻域的改进PSO算法[J].计算机工程，2011，11:20-22.(Yao Canzhong，Yang Jianmei. Improved PSO Algorithm Based on Variety Inertia Weight and Dynamic Neighborhood[J]. Computer Engineering，2011，11:20-22.)

[7] 林国华，胡朝江.序列二次规划法解最优控制问题[J].飞行力学，1994，12(4):45-50.(Lin Guohua，Hu Chaojiang. Sequential Quadratic Programming Method for Solving Optimal Control Problems[J].Flight Dynamics，1994，12(4):45-50.)

[8] 周浩，陈万春，殷兴良.高超声速飞行器滑行航迹优化[J].北京航空航天大学学报，2006，32(5):513-517.(Zhou Hao，Chen Wanchun，Yin Xingliang.Optimization of Glide Trajectory for a Hyper-sonic Vehicle[J].Journal of Beijing University of Aeronautics and Astronautics，2006，32(5): 513-517.)

[9] 郭杰，唐胜景，李响，杨春雷.基于改进粒子群算法的方案飞行弹道优化设计[J].北京理工大学学报，2010，30(6):688-692．(Guo Jie，Tang ShengJing，Li Xiang，Yang Chunlei.Optimum Design of the Project Trajectory Based on an Improved Particle Swarm Optimization[J].Transactions of Beijing Institute of Technology，2010，30(6):688-692．)

The Optimization Design of Glide Trajectory for Guide Bomb with Morphing Swept Wings

ZHAO Ri1SUN Ruisheng1SHEN Jianping2

1. School of Energy and Power Engineering，NUST，Nanjing 210094,China 2. Unit 95856, PLA of China, Nanjing 210028，China

Inordertoimprovetheglidingabilityoftheguidebombwithmorphingsweptwings，animprovedparticleswarmoptimization(PSO)methodisadoptedtoachievetheoptimizationtrajectoryunderthedifferentinitialconditionsofsubsonic,transonicandsupersonic.Theoptimizationresultsbetweenfixedshapeandvariableshapeshowthatthemorphingsweptwingshassignificantextended-rangeeffectundertheinitialconditionsofsupersonic，buttheyhardlyextendrangeundertheinitialconditionsofsubsonic.Theresultscanserveasareferencetotheoveralldesignofguidebombwithmorphingsweptwings.

Guidebomb；Trajectoryoptimization；Morphingsweptwings；Particleswarmoptimization

*国家自然科学基金项目(11176012)；航空科学基金项目(20110159001)

2013-04-28

赵 日(1990-),男，安徽蚌埠人，硕士研究生，主要研究方向为先进弹道理论与控制技术；孙瑞胜(1978-)，男，江苏盐城人，博士，副教授，主要研究方向为先进弹道理论与控制；沈坚平(1962-)，男，上海人，博士，高级工程师，硕士生导师，主要研究方向为航空弹药总体论证、设计和使用。

TJ761.6

A

1006-3242(2014)01-0016-05