捷联惯组历次测试数据分布特性研究

张焕鑫 李学锋

北京航天自动控制研究所，北京 100854



捷联惯组历次测试数据分布特性研究

张焕鑫 李学锋

北京航天自动控制研究所，北京 100854

针对捷联惯组历次测试数据小样本的特点，提出将随机加权法与最大熵法结合应用于捷联惯组历次测试数据的验前分布研究。在总体分布参数形式已知的情况下，根据已有的先验信息，采用随机加权最大熵法获得捷联惯组历次测试数据总体参数的验前分布。结合当前样本信息，利用贝叶斯方法给出捷联惯组历次测试数据的验后分布，揭示捷联惯组历次测试数据的统计特性，减少小样本情况下的统计分析误差。

捷联惯组;随机加权法;最大熵法;历次测试数据;验前分布;小样本

捷联惯导系统已在航天、航空、航海、陆地运输工具等领域得到广泛应用。但捷联惯组的寿命有限，测试程序复杂，测试、标定一次需要较长时间，所以测试次数较少，所得到的历次测试数据均为小样本，使经典的统计分析方法无法满足分析的要求，为后续的统计推断带来一定困难。贝叶斯方法能够充分利用现有信息，解决小样本条件下验前分布的确定问题为后续的建模补偿工作提供分析基础。

在小样本情况下，常利用一些非参数的统计方法，如Bootstrap方法[1]、随机加权法[2]等确定先验分布。文献[3-4]分别利用Bootstrap方法和随机加权法确定捷联惯组历次测试数据总体参数的验前分布，但Bootstrap方法、随机加权法难以直接确定验前分布的参数，大多数情况下，都是直接利用某一分布拟和直方图估计分布参数；而最大熵方法能够较好地处理不完全验前信息的不足和尽量避免主观因素的影响，可以求解连续概率密度函数以替代经典统计学中通过直方图确定概率分布的方法，便于估计分布参数[5]。

因此，本文将随机加权法和最大熵方法相结合应用于对捷联惯组历次测试数据的统计特性分析。首先利用随机加权法对小样本的惯组历次测试数据进行重复采样，然后在二阶矩等式约束下，利用最大熵方法确定验前分布的参数，再结合当前样本利用贝叶斯方法确定验后分布，最后对统计分析结果进行基于验后分布的统计推断，确定其合理性。

1 捷联惯组验前信息的获取

捷联惯组测试数据主要包括3部分：1)出厂前稳定性试验数据；2)交接转运过程的测试数据；3)使用单位的正常测试数据。也就是本文的研究对象:历次测试数据(或者称为当前测试信息)。捷联惯组性能相对比较稳定，在一段时间内，在没有经过检修、长途运输，而且环境因素没有显著变化的情况下，其历次测试数据一般符合正态分布[3]。因此，可以设捷联惯组历次测试数据的总体分布形式为正态分布。

捷联惯组验前信息的获取主要依靠前2部分测试数据，通称为验前测试数据(或验前信息)。本文根据实际状况采用第一部分的测试数据作为验前信息。捷联惯组测试次数较少，因此验前信息的使用非常重要。由于捷联惯组已经得到广泛应用，积累了大量的验前测试数据和历次测试数据，这都为捷联惯组历次测试数据验前分布的研究和确定提供了充足可靠的依据。

2 验前分布确定

设x1,x2,…,xn是来自正态分布N(θ,σ2)的一个样本观察值，其中均值θ未知，σ2已知，Bayes方法认为总体均值θ为随机变量。如果可以提供关于θ的历史数据，那么θ的分布可以确定。

2.1 最大熵验前密度

熵是衡量一个随机变量取值的不确定性程度。随机变量θ的概率密度π(θ)的信息熵可以定义为:

(1)

式中,R为随机变量θ的变化空间。

概率密度π(θ)满足以下约束条件：

(2)

(3)

其中，式(3)中gi(θ)为已知函数，mi为参数θ的i阶样本矩。在此约束下，令熵取最大值，此时的π(θ)作为θ的验前密度。这就是所谓最大熵验前密度的确定方法。θ的验前密度(最大熵验前分布)可表示为：

(4)

其中，待定系数λi可由方程(2)和(3)确定。特别地，当i=2时，验前函数可表示为一元正态分布，即在二阶矩等式约束下只要确定参数θ的期望和方差就可以确定验前的具体形式[6]。

2.2 随机加权最大熵验前分布的确定

在二阶矩等式约束下，利用随机加权最大熵法确定验前分布，可采用下列步骤：

1) 考虑总体均值θ的估计偏差：

(5)

2) 分别构造并产生N组Tn的随机加权统计量：

(6)

其中v(i)=(v1(i),v2(i),…,vn(i))是取自Dirichlet分布的随机变量。

3) 以Dn(i)，i=1,…,N作为Tn的估计，由此得到参数θ的一组随机加权估计：

(7)

3 验后分布确定

在没有样本信息时，只能根据验前分布对θ作出推断。在有了样本(历次测试数据)之后，就要将样本与验前分布π(θ)进一步综合，设x1,x2,…,xn是来自正态分布N(θ,σ2)的一个样本观察值。其中σ2已知。此样本的似然函数为：

(8)

由于已知θ的先验分布为正态分布N(μ,τ2)：

-∞<θ<+∞

(9)

其中μ与τ2为已知，由此可以写出样本x与参数θ的联合密度函数：

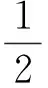
(10)

则有

(11)

(12)

上面两式相除，即得θ的后验分布

(13)

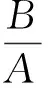
这说明了正态均值(方差已知)的共轭先验分布是正态分布。

4 贝叶斯统计推断

未知参数θ的后验分布π(θ|x)是集3种信息(总体，样本和先验)于一身，它包含了θ的所有可供利用的信息，所以有关θ的估计和假设检验等统计推断都按一定方式从后验分布π(θ|x)中提取信息。

4.1 贝叶斯估计

参数θ的贝叶斯估计有3种：最大后验估计、θ的后验中位数估计和θ的后验期望估计[6]。在一般场合下，这3种贝叶斯估计是不同的，当后验密度函数为对称时，这3种贝叶斯估计重合，是相同的。

(14)

4.2 假设检验

H0:θ=θ0，H1:θ≠θ0

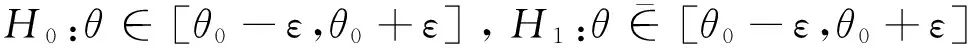
其中ε是很小的数，使得[θ0-ε,θ0+ε]与θ=θ0难以辨别。

对简单假设H0:θ=θ0作贝叶斯检验时不能采用连续密度函数作为先验分布，因为任何这种先验将使θ=θ0的先验概率为0，从而后验概率也为0，所以一个有效的方法是对θ=θ0给一验前概率π0，而对θ≠θ0给一个加权的密度π1g1(θ)，g1(θ)～N(μg,v2)，θ的先验密度为

π(θ)=π0Iθ0(θ)+π1g1(θ)

(15)

其中Iθ0(θ)为θ=θ0的示性函数，π0为近似的实际假设H0:θ∈[θ0-ε,θ0+ε]上的先验概率。

(16)

其中

则有

(17)

其中

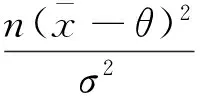
利用正态分布的正则性，可得

(18)

从而简单原假设与复杂备选假设(记为Θ1={θ≠θ0})的后验概率分别为

后验机会比为

从而贝叶斯因子为

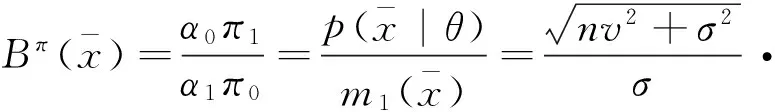
(19)

对于H1:θ≠θ0上的先验密度g1(θ)，一般地，参数θ接近于θ0比远离θ0更为可能，所以一般取μg=θ0，v2一般可以取2σ2，则有

(20)

5 实例分析

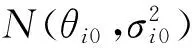
表1 验前历次测试数据

表2 验前分布参数

已知该此4套捷联惯组同一误差系数的验后测试样本如表3所示。

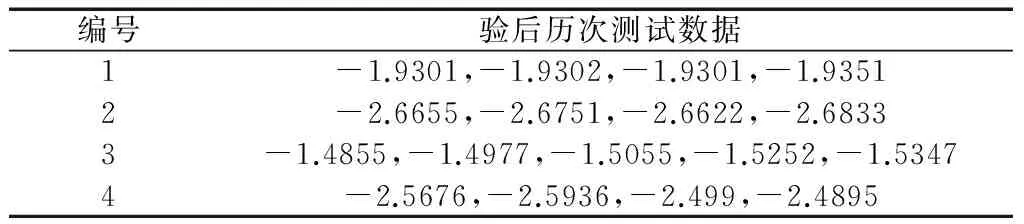
表3 验后历次测试数据

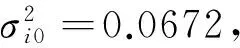
表4 验后分布参数

由这4套惯组得到的用于假设检验的当前测试样本如表5所示。

表5 当前历次测试数据

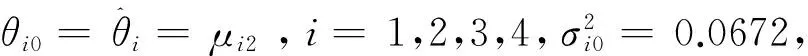
表6 贝叶斯因子

由于贝叶斯因子均大于1，所以接受原假设：H0:θ=θi0，i=1,2,3,4，这表明此误差系数总体分布的参数符合正态分布，不同惯组其分布参数不同，同时分析结果也表明此误差系数总体分布设为正态分布的合理性。

6 结论

将随机加权最大熵法应用于对捷联惯组历次测试数据的统计特性分析，既能利用随机加权法有效扩充测试次数的样本信息，也能采用最大熵法充分利用样本信息，尽量避免主观因素的影响，有效减小验前信息不确定性的影响，在验后分布的基础上进行统计推断，可为进一步的捷联惯组历次测试数据时间序列建模与预报提供分析基础。

[1] Efron B, Stein C.The Jackknife Estimate of Variance [J]. Operations Research,1981, (9):586-596.

[2] 郑钟国. 随机加权法[J].应用数学学报,1987,10(2):247-253.(ZHENG Zhongguo. Random Weighting Method[J]. Acta Mathematicae Applicatae Sinica,1987,10(2):247-253.)

[3] 徐军辉,肖正林,钱培贤.基于Bootstrap 方法的捷联惯组历次测试数据验前分布研究[J].宇航学报,2006,27(3):407-411. (XU Junhui, XIAO Zhenglin, QIAN Peixian. The Prior Distribution Study of SIMU Successive Test Data Baesd on Bootstrap Method[J]. Journal of Astronautics, 2006,27(3):407-411.)

[4] 徐军辉,钱培贤，李辉.基于随机加权法的捷联惯组历次测试数据验前分布研究[J]. 战术导弹技术, 2007,(3):71-73.( XU Junhui, QIAN Peixian, LI Hui. The Population Parameter Prior Distribution Study of Successive Test Data of SIMU Based on Random Weighting Method[J]. Tactical Missile Technology,2007,(3):71-73.)

[5] 张守玉, 刘博强.小样本下装备平均维修时间验前分布确定方法研究[J].装备指挥技术学院学报, 2010,5(21):353-360.(ZHANG Shouyu,LIU B0qiang. Study on Ascertainment Method of Prior Distribution for MTTR on Small Samples[J]. Journal of the Academy of Equipment Command and Technology, 2010,5(21):353-360.)

[6] 凌光, 戴怡, 王仲民.面向数控系统可靠性评估的最大熵先验信息解[J].机械工程学报,2008,48(6):157-161.(LING Guang, DAI Yi, WANG Zhongmin. Maximum Entropy Prior Information Solution for Numerical Control System Reliability Assessment[J]. Journal of Mechanical Engineering, 2008,48(6):157-161.)

The Analysis of SIMU Successive Test Data Based on Combined Model

ZHANG Huanxin LI Xuefeng

Beijing Aerospace Automatic Control Institute, Beijing 100854, China

Aimingatthesmallsamplefeaturesofstrapdowninertialmeasurementunit(SIMU)successivetestdata,therandomweightingmethodandmaximumentropymethodareusedtogetthepriordistributionofpopulationparameterofsuccessivetestdataofSIMUwithpriorinformation,whenthedistributionformofpopulationparameterisknown.TheBayesianmethodisadoptedtodeterminetheposteriordistributionwiththepriorinformationandcurrentinformation,andthestatisticalcharacteristicofSIMUsuccessivetestdataarerevealedandtheerrorsofstatisticalanalysisinthecaseofsmallsamplesarereduced.

SIMU;Randomweightingmethod;Maximumentropymethod;Successivetestdata;Priordistribution;Smallsample

2013-02-04

张焕鑫(1984-),男，山东昌邑人，博士研究生，主要研究方向为控制系统综合与小样本建模；李学锋(1966-)，男，陕西汉中人，研究员，博士研究生导师，主要研究方向为导航、制导与控制。

TJ765.1

A

1006-3242(2014)01-0040-04