考虑气弹稳定性的无人飞行器结构和稳定系统协同设计

范奎武

海军驻航天一院代表室, 北京 100076



考虑气弹稳定性的无人飞行器结构和稳定系统协同设计

范奎武

海军驻航天一院代表室, 北京 100076

针对带自动控制系统的机动无人飞行器，介绍考虑气动弹性稳定性需求时结构和稳定系统协同设计的求解问题，描述了实现这种设计理念的模型和方法，给出了求解协同设计问题的例子以及保证带自动控制系统的机动无人飞行器气动弹性稳定性的建议。

无人飞行器;结构;自动控制系统;稳定回路;气动弹性;稳定性

在设计机动无人飞行器时，除了考虑强度、刚度、稳定性这些机身结构的传统限制外，还应该考虑由飞行控制系统的工作条件引出的限制[1～3]。

机动无人飞行器结构弹性对控制系统工作的影响首先表现在“弹性飞行器自动控制系统”回路中出现自振，导致自动控制系统的通道被信号的高频分量“堵塞”，从而对飞行器的可控性产生不利影响，破坏机上设备的正常工作状态，使其运行品质明显降低直至损坏。随着飞行器速度、升限和机动过载的增长、控制系统快速性的提高，以及刚度较小舵机的使用和发动机工作形成的大振动过载，在“弹性飞行器自动控制系统”回路中出现自振的危险性还在增长[4～5]。

当控制系统参数已知时，飞行器气动弹性稳定性问题已有比较好的解决方法。但是飞行器结构和自动控制系统协同设计在工程应用中仍存在许多问题需要解决，因此研究该领域内的新方法尤为迫切，本文就介绍一种方法[6]。

1 问题的提出与通用求解方法

机动无人飞行器自动控制系统和结构协同设计，指在已知无人机机体的基准设计(工艺方案和控制系统的总体特征、稳定回路的精度、快速性、飞行状态参数、结构强度、稳定性需求、气动弹性稳定性需求和限制)的条件下，获得针对无人机的结构以及结构参数、稳定系统参数的协调解决方案。

采用一种迭代方法解决结构与控制系统的协同设计问题，它包含3个阶段：

1)选择控制系统的结构和稳定回路的主要参数；

2)飞行器结构和稳定系统分开设计。该阶段的目的是获取无人飞行器的设计(工艺方案)，以最优的方式满足结构和工艺完善的需求，以及从飞行器稳定与控制规律、质量、尺寸、造价的角度出发，设计合理的自动稳定系统。在遵守第一阶段形成的需求前提下，在第二阶段用传统的最可以接受的方法进行子系统的设计；

3)协调无人飞行器结构参数和稳定系统参数，以满足带自动控制系统的飞行器气动弹性稳定性的需求。

2 结构和主要参数选择

稳定回路包括飞行器自身、反馈、计算和执行装置，主要用途是改进机动无人飞行器对控制指令的响应品质：增加快速性、减小超调量和过渡过程的阻尼时间。

大多数机动无人飞行器结构的扭转刚度很高，滚动通道内出现自振的问题不像俯仰、偏航通道内的那么严重，因此对轴对称飞行器而言，可以只研究相类似的俯仰和偏航通道。由于舵面上的升力较小，可以忽略。对于轴对称飞行器，不考虑主发动机喷射流束作用下机体旋转时出现的哥氏加速度，可以写出刚性飞行器俯仰通道内针对角速度ω和线性加速度W的传递函数(在安装角速度传感器和线性加速度传感器位置处)：

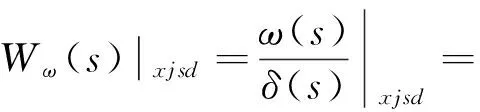
(1)

(2)

现代“面—空”类机动无人飞行器典型俯仰(偏航)通道稳定系统通常包含角速度反馈回路和线性加速度反馈回路，图1所示为典型的两层反馈稳定系统，对静稳定和静不稳定飞行器均可适用。由角速度ω反馈组成的回路通常称为阻尼回路，由线性加速度W反馈组成的回路称为稳定回路。

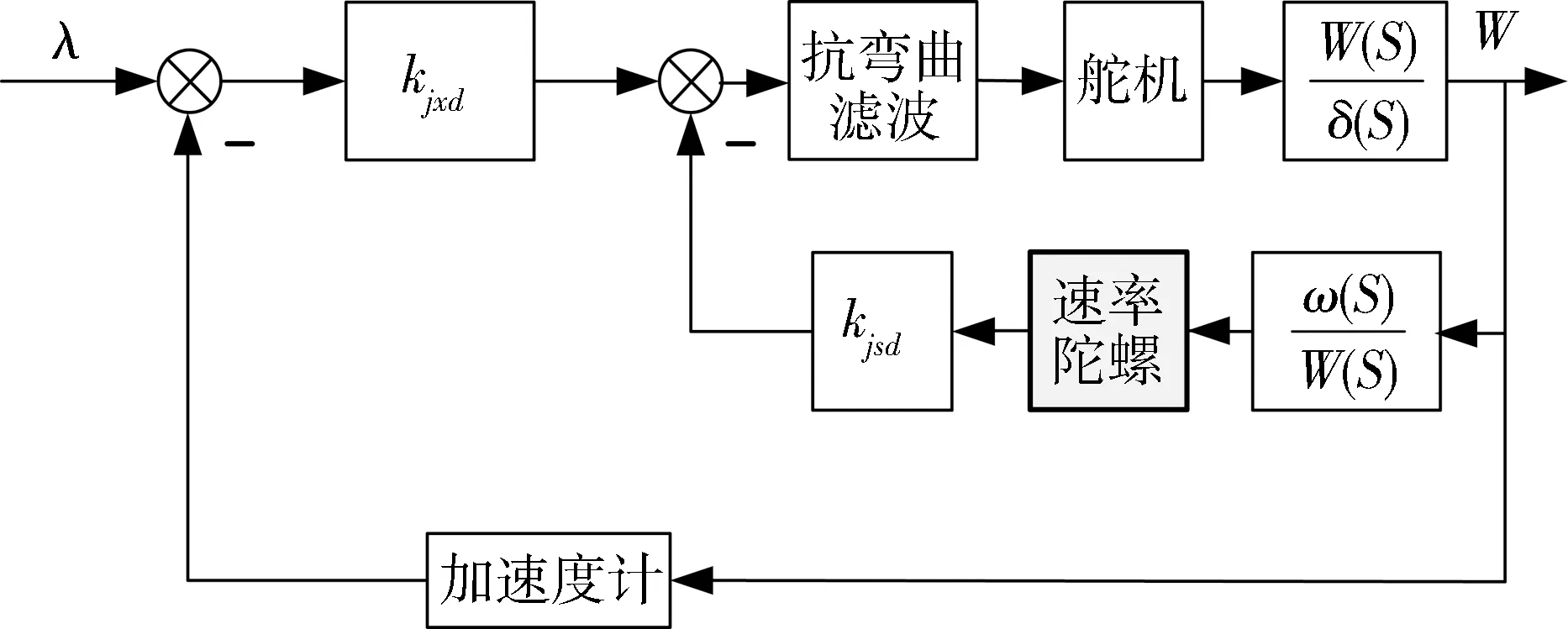
图1 飞行器稳定系统结构图(λ为控制指令；kjsd,kjxd分别为速率陀螺反馈回路和加速度计反馈回路的放大系数)

闭环稳定系统(见图1)的传递函数可以表示成放大系数为kwd、阻尼指标ξwd和时间常数Twd的振荡环节形式：

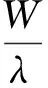
(3)

闭环稳定系统的固有频率ωwd和阻尼指标ξwd确定其对阶跃式控制指令的响应时间τ和超调量Δ1的大小(过渡过程的参数τ和Δ1在无人飞行器研制任务书中给出)。通过选择合适的参数kjsd和kjxd，可以影响传递函数Wwd(s)的参数和闭环系统响应特性，从而使无人飞行器的动态特性得到改进。因此，根据无人飞行器的动态特性和稳定系统自身稳定性这两方面的需求来选择参数kjsd和kjxd。

为保证稳定系统在机体弹性振动频率上的稳定性 ，引入抑制幅值的滤波器，其传递函数为

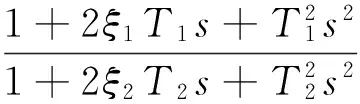
(4)

时间常数T2/T1的比值通常位于0.5～2之间，阻尼系数ξ1=0～0.2和ξ2=0.3～1。抗弯曲滤波器往抑制无人飞行器机体弯曲振动一阶振型频率上调整，必要时往二阶振型频率上调整。

3 结构参数与稳定系统之间的匹配

飞行器气动弹性的计算模型与最重要的运动形式的选择有关。机动无人飞行器的这类运动主要是舵面的弯曲和扭转振动及机体的一阶和二阶弯曲振动，通过机体的弯曲振动考虑机翼的低阶振动。

根据自由梁-机体(带翼)自身承载与机体弹性联结的其它梁-舵的计算方案，考虑到所选择的振型，按照给定振型方法组成的方程组如下：

(5)

式中，mij,hii和gii分别为结构的惯性、阻尼和刚度系数；dij和bij分别为阻尼和刚度的空气动力系数；广义坐标q1和q2分别表示舵面的弯曲和扭转；q3和q4分别为机体的一阶和二阶弯曲。

广义坐标q2是舵偏角，记为δ，由方程组(5)可以确定它到广义坐标矢量q的任意一个分量qi的传递函数。

(6)

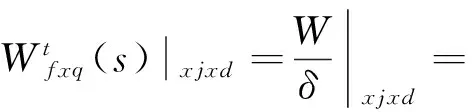
(7)

求解上述问题的迭代方法步骤如下。

在第一阶段，研究飞行器与自动控制系统的相互作用，在不满足气动弹性稳定性需求的情况下，制定能保证稳定性的措施，这些措施既可以是无人机结构方面的，也可以是稳定系统方面的。在第一种情况下调整无人飞行器结构的质量—惯性、阻尼和刚度特性，在第二种情况下调整稳定系统的参数。

为了在考虑由控制系统施加的限制条件下求解无人飞行器结构的合理设计问题，采用结构—参数最优化方法，该方法使用空气自弹性系统(弹性飞行器与自动控制系统联合)标准，在考虑由结构与自动控制系统相互影响决定的工作限制情况下，实现飞行器结构中质量与刚度的最优分配。利用该方法解决如下问题：

1)在一般情况下，使用结构工作的一组数学模型和一组静态的和动态的使用限制(强度、稳定性等)，求解多层最优化问题，根据求解结果，形成飞行器的结构标准；2)把飞行器结构的标准变换成新的标准即气动自动弹性系统标准；3)把无人飞行器机身设计-工艺方案与新标准结合，选择合理的方案对它们进行优化。

既然结构自身的振动对带自动控制系统的飞行器气动弹性稳定性起确定性作用，那么作为由弹性飞行器和自动控制系统联合工作带来的附加限制，使用对飞行器固有振动特征的限制，通常是对频率的限制：flmin≤fl≤flmax,l=1,2,…,L*(fl为飞行器的第l阶固有振动频率；flmin,flmax为fl变化范围的边界；L*为所研究的频率数量)。

自动控制系统的参数调整与传感器沿无人飞行器机体长度安放位置的最优化有关，与抑制无人飞行器最危险振型的新型滤波器的参数调整或者是设置有关，与舵机频率特性的变化有关。

与无人飞行器机体设计(工艺方案或者是稳定系统参数调整)有关的问题，在飞行器结构和自动控制系统稳定系统参数协调设计的第二阶段解决，在此之后对带自动控制系统的飞行器气动弹性稳定性进行迭代研究。当满足需求时，就结束迭代设计过程。

4 协同设计实例

对某正常式气动布局的机动无人飞行器，使用所提出的迭代方法来解决弹性机体结构和稳定系统的联合设计问题，以说明方法的有效性和设计结果的可信性。其空气动力控制机构是全动舵，控制系统的结构如图2(a)所示。稳定系统的角速度传感器和加速度传感器安装在飞行器机体一阶弯曲振动弹性线的腹点附近。

图2(a) 无人飞行器的外型

图2(b) 固有弯曲振动的振型

无人飞行器固有弯曲振动的特征见图2(b)：

带燃料的无人飞行器(273千克):一阶频率33.3Hz，振型为曲线1；二阶为80.3Hz，曲线3。

无燃料的无人飞行器(185千克):一阶频率39.5Hz，振型为曲线2；二阶为96.7Hz，曲线4。

在2种情况下，弯曲振动的对数衰减量相同，都是0.05。

图3 “弹性飞行器自动控制系统”回路稳定性保证措施的有效性研究

5 结论

本文介绍了考虑气动弹性稳定性需求的弹性无人飞行器和自动控制系统结构协同设计问题和迭代求解方法，给出了描述问题的数学模型，叙述了既考虑对机身结构传统的强度和稳定性的需求、也考虑与保证有控飞行器气动弹性稳定性有关的附加限制的机身结构参数最优化方法。最后给出了求解弹性无人飞行器结构参数和自动控制系统协同问题的设计实例，确认了所提出方法的有效性和设计结果的可信性。

在所得到的求解无人飞行器机体的设计，即工艺方案参数和稳定系统参数协同问题的基础上，给出了保证带自动控制系统的机动无人飞行器气动弹性稳定性的具体建议：1)安装针对机体弯曲振动的滤波器；2)更合理地配置自动控制系统的传感器； 3)修正舵机的频率特性； 4)为了以必要的方式变化飞行器结构的固有振动频率，对其进行补充加工。

[1] 周慧钟,李忠应,王谨玫,编著.有翼导弹飞行动力学[M].航空专业教材编审组，1983.

[2] 陈士橹，等.合编 近代飞行器飞行力学[M].西北工业大学出版社，1987.

[3] HW伏欣，沈克杨，译.气动弹性力学原理[M].上海科学技术文献出版社，1982.

[4] 杨超.飞行器气动弹性原理[M].北京航空航天大学出版社，2011.

[5] В.И.Морозов，А.Т.Пономарев，О.В.Рысев.Матема- тическое моделирование сложных аэроупругих систем [M].М：Физматлит 1995.

[6] С.Г.Парафесь.Совместное проектирование констру- кциии системы стабилизации беспилотного летательн-ого аппарата с учётом требований аэроупругой устой- чивости [J]. Полёт 2012(8): 35-42.

A Collaborative Designing of the Structure and Stabilization System of Unmanned Aircraft with the Requirements of Aeroelastic Stability

FAN Kuiwu

Representatives Office of Navy of CALT, Beijing 100076, China

Anapproachtothesolutionofthecollaborativedesignofthestructureandstabilizationsystemofthemaneuverunmannedaircraftwiththerequirementsofaeroelasticstabilityisintroduced,andtheimplementationofmodelsandmethodsaredescribed.Acasestudyofsolvingtheproblemofcollaborativedesignaswellastherecommendationstoprovidetheaeroelasticstabilityofthemaneuverunmannedaircraftwiththeautomaticcontrolsystem(ACS)aregiven.

Unmannedaircraft;Construction;Automaticcontrolsystem；Stabilizationloop;Aeroelasticstability；Design

2014-03-12

范奎武(1964-),男，山东冠县人，博士后，高级工程师，主要研究方向为飞行器总体设计、制导与控制。

TP316.2

A

1006-3242(2014)03-0066-05