基于模糊控制的有限时间收敛制导律

赵海斌 李 伶 孙 胜

北京航天自动控制研究所,北京 100854



基于模糊控制的有限时间收敛制导律

赵海斌 李 伶 孙 胜

北京航天自动控制研究所,北京 100854

针对有限时间收敛制导律中非线性控制项参数的调节，提出了一种基于模糊控制理论的改进有限时间收敛制导律。该方法结合模糊控制理论和有限时间收敛制导规律，首先给出制导参数在有限时间收敛的前提下需要满足的范围，分析参数变化对系统收敛的影响效果；其次根据模糊控制理论设计模糊控制器实现参数自适应调节。数学仿真结果表明此设计可以有效地提高系统收敛速度并且抑制末端过载的高频抖振。

导引律；有限时间收敛；模糊逻辑

采用准平行接近方法设计的导引规律只能保证当时间趋于无穷时视线角速率趋于0，从理论角度讲是不完善的，因此研究有限时间收敛的制导规律很有价值[1]。文献[2]基于有限时间稳定性定理，给出了有限时间稳定的高阶滑模导引规律；文献[3]基于二维平面目标—导弹相对运动模型，根据非线性控制系统有限时间稳定性理论，研究有限时间收敛导引方法，但是视线角速率收敛速度以及收敛的稳态效果对参数的依赖性很强。因此，寻求一种合理的自适应有限时间收敛制导律具有研究价值。

本文采用模糊控制算法实现参数自适应调节。该方法具有适应被控对象非线性和时变性的特点，不需要控制系统精确的数学模型。模糊推理本质上是将给定输入空间通过模糊逻辑的方法映射到特定输出空间的计算过程。最常见的模糊推理系统有三类，其中具有模糊产生器和模糊消除器的模糊逻辑系统(Mamdani)设计方法在工程应用中最为广泛[4]。根据有限时间收敛理论中参数所需要满足的范围以及参数变化对导引效果的影响，通过合理化设计模糊控制器，自适应调节导引参数，有效减小收敛时间、抑制控制量抖动，从而保证命中精度。最后通过一个数学仿真实例验证该制导规律设计的正确性。

1 有限时间收敛制导律

图1 弹目相对运动关系

由上图可以推导弹目相对运动方程

(1)

(2)

对上两式分别求导，并代入整理得到

(3)

(4)

其中，导弹加速度在视线方向上的分量为

(5)

导弹加速度在法向上的分量为

(6)

(7)

文献[3]提出了一种基于Lyapunov意义下的有限时间稳定性定义，并基于该定义推导了一种有限时间收敛制导律，其形式如下：

(8)

(9)

其中x(0),R(0)分别代表初始时刻视线角速度与相对距离，详细证明可见参考文献[3]。从形式上可以看出该制导律实际上可以理解成比例导引与非线性导引的复合导引，是一类非光滑控制律。符号函数的加入使得导引律具有Bang-Bang控制快速调节的特点；指数函数的加入使得导引律具有平滑收敛的特点。当η=0时该导引律是滑模变结构形式，证明可见文献[5]。如果参数设计不当，调节速度过快容易诱发系统控制量高频抖动。在抑制高频抖动方面提出了许多改进方法，如边界层设计、连续函数近似、滤波方法等[6]。本文不同于上述方法，而是从参数调节入手，抑制高频抖动。

下面从数学角度分析参数变化对收敛效果产生的影响。通过分析收敛时间tc满足的不等式(9)可以得出，在给定初始状态下，参数β,η对收敛时间产生重要影响。定义

(10)

图2 不同ν条件下g(ν)随a的变化曲线

2 模糊控制器设计

Mamdani系统(结构如图 3所示[7])包括模糊化、模糊推理和清晰化3个环节。

图3 模糊控制器系统框图

2.1 模糊化

(11)

(12)

图4 输入输出变量隶属度函数

2.2 模糊推理

根据第1节中参数β,η对收敛时间tc的影响分析，可以制订模糊控制规则库。例如，如果视线角速率正大并且视线角加速率也正大，缩短收敛时间的策略为增大非线性控制项系数，因此β应增大，η应减小。表1和2分别列出了参数β和η的模糊控制规则。

表1 参数β模糊控制规则

表2 参数η模糊控制规则

2.3 清晰化

本文采用加权平均法，即重心法。该方法既突出了主要信息，又兼顾了其它信息，贴近实际情况，从而应用较为广泛。计算方法如下：

(13)

其中，n=15为模糊控制规则条数，βk,ηk为各参数的第k条模糊推理结果，νk为模糊推理规则库中的第k条模糊规则的条件真值。

3 仿真分析

图5和 6分别反映了过载和视线角速率在整个导引过程和导引末端的变化曲线，比较2种方法，可以看出通过自适应调节后的这两个物理量在导引前期快速收敛到0附近、在导引后期有效抑制控制量抖动。图 7反映了模糊控制器的输入和输出在整个导引过程中的变化曲线，按照模糊逻辑正确调节参数。

图5 过载、视线角速率随时间变化曲线

图6 导引末端过载、视线角速率随时间变化曲线

图7(a) 模糊控制器参数归一化能量随时间变化曲线

图7(b) 模糊控制器参数归一化能量变化率随时间变化曲线

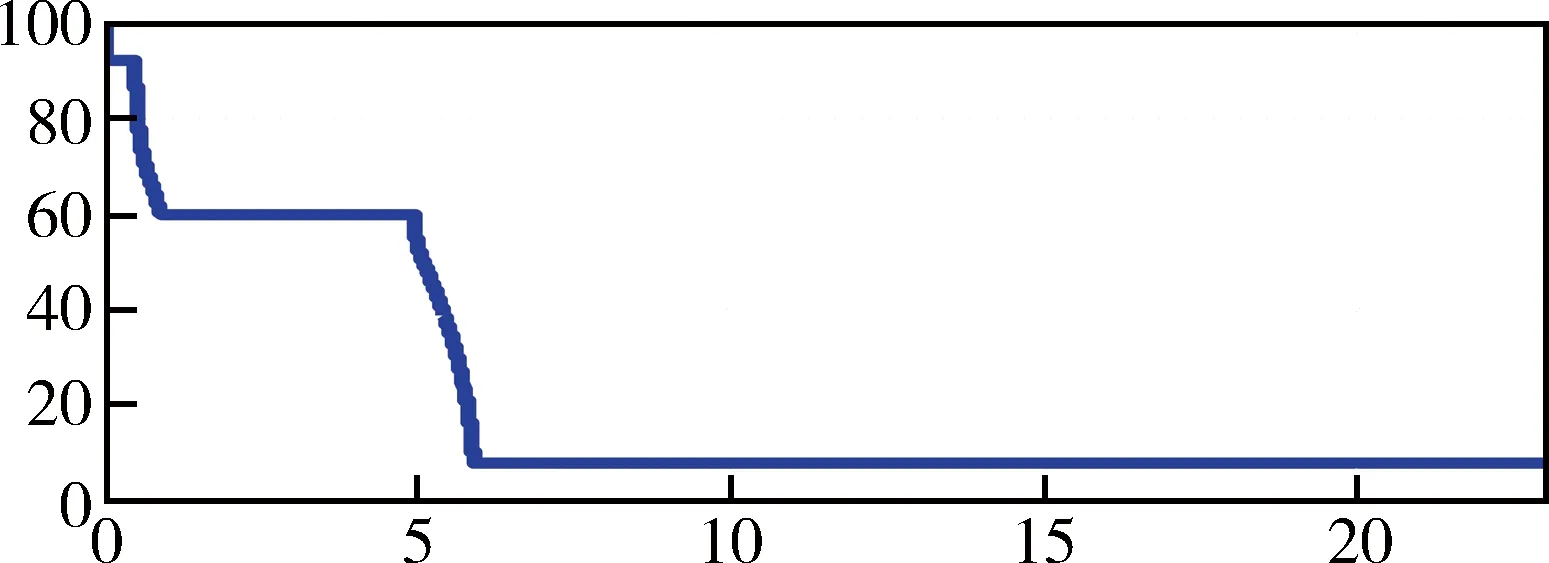
图7(c) 模糊控制器参数β随时间变化曲线

4 结论

提出了一种基于模糊控制理论的有限时间收敛制导律。首先明确参数需要满足的范围，根据能量与能量变化率的变化，通过模糊控制理论来调节参数。仿真结果表明，该制导律通过自适应地调节参数，可以充分利用好控制变量，加快制导系统收敛速度的同时抑制末端抖动，从而有效提高制导系统性能。通过以上研究表明，在初始状态一定、控制量不饱和的条件下，设计一个确保制导系统有限时间收敛且应用方便、参数具有自适应的智能导引律更具有工程应用价值。

[1] 孙胜,张华明,周荻.末端导引律综述[J].航天控制,2012，30(1):86-96.(Sun Sheng, Zhang Huaming, Zhou Di. A Survey of Terminal Guidance Law[J]. Aerospace Control,2012，30(1):86-96.)

[2] Shtessel Y,Shkolnikov I. Integrated Guidance and Control of Advanced Interceptors Using Second Order Sliding Models[C]. IEEE Conference on Decision and Control, Maui, USA, 2003.

[3] 孙胜.有限时间收敛寻的导引律[D].哈尔滨:哈尔滨工业大学,2010.

[4] 易继锴,侯媛彬.智能控制技术[M].北京:北京工业大学出版社,1999.

[5] 周荻.寻的导弹新型导引规律[M].北京：国防工业出版社，2002.

[6] K.David Young, Vadim I.Utkin, Ümit Özgüner. A Control Engineer’s Guide to Sliding Mode Control[C]. IEEE Conference onVariable Structure Systems, Calif, USA, 1996.

[7] 吴晓莉,林哲辉，等.MATLAB辅助模糊系统设计[M].西安：西安电子科技大学出版社，2002.

Guidance Law with Finite Time Convergence Based on Fuzzy Logic

ZHAO Haibin LI Ling SUN Sheng

Beijing Aerospace Automatic Control Institute, Beijing 100854, China

Anewmethodbasedonfuzzylogicisintroducedtoadjustparametersofnonlinearcontrolinguidancelawwithfinitetimeconvergence.Afinitetimeconvergencetheoryisusedtoobtainboundofparameters,andthentheinfluencesforconvergencearediscussed.Onthebasisoffuzzylogic,anadaptivecontrollerisdesigned,whichisaccordingtoboundandinfluencesmentioned.Thesimulationresultsshowthattheconvergenceofthisimprovedguidancelawiseffectiveandhighfrequencychatteringofaccelerationisrestrained.

Guidancelaw;Finitetimeconvergence;Fuzzylogic

2013-03-12

赵海斌(1989-)，男，北京人，硕士研究生，主要研究方向为飞行器制导与控制；李 伶(1972-)，女，湖北赤壁人，博士，研究员，主要研究方向为飞行器制导与控制、仿真技术；孙 胜(1982-)，男，江西高安人，博士，工程师，主要研究方向为飞行器制导与控制。

V448.133

A

1006-3242(2014)03-0033-05