基于观测方程的捷联系统工具误差可观测性分析

高叶叶 李华滨 李 伶 宋维军

北京航天自动控制研究所,北京 100854



基于观测方程的捷联系统工具误差可观测性分析

高叶叶 李华滨 李 伶 宋维军

北京航天自动控制研究所,北京 100854

针对捷联导航系统工具误差可观测性问题，建立相对较完整的激光惯组误差模型，并在惯性系中推导了捷联惯导工具误差的观测方程。利用奇异值分解理论(SVD)分析误差系数的可观测性，并以仿真程序生成的弹道为例说明了分析捷联系统工具误差可观测性的过程及特点。

捷联惯导；工具误差；可观测性；奇异值分解

随着计算机技术和惯性器件的飞速发展，捷联惯性导航系统在上世纪80年代已逐渐进入实际应用阶段。捷联惯导系统最大的特点是用数学平台代替物理平台,避免了平台式惯导系统复杂的物理实体平台,且捷联惯导系统的可靠性高，体积小，成本低,还可通过冗余技术提高系统的容错能力[1]。因此，捷联系统在导弹惯性导航领域得到了广泛应用。

对于应用捷联惯性导航系统的导弹来说，影响其命中精度的因素有很多，如制导工具误差、方法误差、初始对准误差等，其中，制导工具误差影响最大。实践证明，对惯性测量元件的工具误差进行补偿是提高导弹命中精度切实可行的方法。捷联系统工具误差系数的可观测性是进行工具误差系数分离、实现误差补偿的基础。捷联系统中用姿态解算矩阵代替物理平台，而姿态阵解算过程与陀螺仪输出密切相关，因此陀螺仪误差密切耦合于捷联系统解算出的各物理量中，同时加速度计的测量输出也存在误差，使工具误差项的可观测性更为复杂。误差的可观测性直接影响误差项的估值效果，因此开展针对捷联系统的工具误差可观测性研究很有必要。

本文通过建立激光捷联惯组的误差模型，推导计算了捷联系统工具误差与遥外差之间的线性关系，即得到工具误差的可观测矩阵。介绍了奇异值分解理论(SVD)在捷联系统误差系数可观测性方面的应用；最后选取一段仿真程序得到的弹道应用SVD分析捷联系统工具误差的可观测性。为捷联系统误差分离的研究工作提供了参考。

1 建立惯组工具误差模型

本文以2个两轴陀螺仪正交安装的捷联惯组为研究对象，利用其2个双敏感轴构成三轴正交系，其敏感轴与飞行器坐标轴平行，敏感测量飞行器角速度在弹体坐标系3个轴方向的投影，其误差主要包括陀螺零次项漂移、一次项误差及安装误差，其中安装误差为3个敏感轴安装不垂直引起的输出误差。因此，建立激光捷联惯组陀螺仪误差模型如下：

(1)

其中，αx,αy,αz为陀螺仪输出值的偏差在弹体系坐标轴方向的投影；ωx1,ωy1,ωz1为飞行器角速度在弹体系坐标轴方向的投影；egij(i,j=x,y,z)为陀螺仪一次项误差及安装误差系数。

捷联系统中，加速度计测量值为弹体系视加速度，其误差模型主要包括零次项误差、一次项误差、安装误差项与二次项误差。建立误差模型如下：

(2)

2 计算观测矩阵

理论论证与飞行实践表明，捷联系统工具误差与遥外差之间可近似认为是线性关系，利用该关系建立观测方程。

捷联系统中通过求解飞行器体轴转动的运动学方程，得出姿态转换矩阵，从而建立起数学平台，实现弹体系到惯性系的转换。姿态阵解算过程与陀螺仪输出相关，因此陀螺仪误差密切耦合于捷联系统解算出的各物理量中。另外，除陀螺仪引起的误差外，加速度计本身存在漂移，加速度计在安装时存在不对准情况，也导致视加速度的测量值存在误差。

综上，由陀螺仪测量误差间接引起及加速度计测量误差直接导致的捷联系统视加速度偏差总和可表示为：

(3)

其中，陀螺仪引起的视加速度测量偏差为：

(4)

(5)

(6)

其中，D为27×1维工具误差系数矩阵，式(6)即为遥外差与误差系数的线性关系式，SV为捷联系统工具误差的观测矩阵。

3 误差系数可观测性

观测矩阵包含了工具误差可观测性的全部信息，因此研究误差的可观测性即研究其可观测性矩阵。文献[2]通过对捷联系统误差状态进行可观测性的研究，表明动态系统的可观测性矩阵奇异值的大小能用于定量分析系统可观测性,定性分析系统可观测度的大小。分别计算奇异值对应的误差项的值，可具体分析每一项误差的可观测性，对应的奇异值越小，则该项误差系数的可观测性越差。

矩阵的奇异值分解：

设A∈Cm×n,rankA=r>0，则A有奇异值分解：

(7)

其中，U为m阶酉矩阵，V为n阶酉矩阵，∑=diag(σ1,σ2,…,σr),σ1≥σ2≥…≥σr>0是A的r个正奇异值。

将该方法应用到捷联系统工具误差可观测性研究，对前文所得可观测性矩阵的奇异值分解如下：

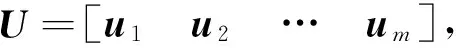
(8)

则有：

(9)

若σn>0，则：

(10)

选取

(11)

认为σi对应的误差项不可观测。其中α为实数，其值根据工程需要确定。

4 仿真算例

利用仿真程序生成一段弹道，其弹体系角速度与视加速度分别如图1和2所示。

图1 弹体系角速度

图2 弹体系视加速度

利用捷联系统六自由度弹道仿真程序仿真遥、外测数据，计算该弹道对应环境函数。对环境函数进行奇异值分解，得奇异值见表1。

表1 观测矩阵的奇异值

根据奇异值整体情况，选取奇异值

即σi(i=19,20,…,27)对应的误差项为不可观测项。将σi由小到大排列，根据式(10)分别计算这9个奇异值对应的误差系数值。下面以图3(a)，即σ27=0.02191为例说明奇异值与误差系数项可观性的关系，其对应项为第10项误差，该项误差系数对应的奇异值极小，认为该项误差系数不可观测。如此类推，图3(b)中奇异值对应的不可观测误差系数项为第20和21项，即egxy和egxz。综合奇异值对应的误差系数值，不可观测项为kayy，kayz，kazx，kazy，kazz，egxx，egxy，egxz，egyy，egyz，egzy，egzz。

另外，在上述误差项中，对于第20与21项，即egxy和egxz，该两项误差在同一个奇异值计算结果中，总是数值基本相等，符号相反，因此，可判断该两项误差对应的观测向量为线性相关关系。同理还有egyy与egyz，egzy与egzz，kayy与kayz，kazy与kazz。

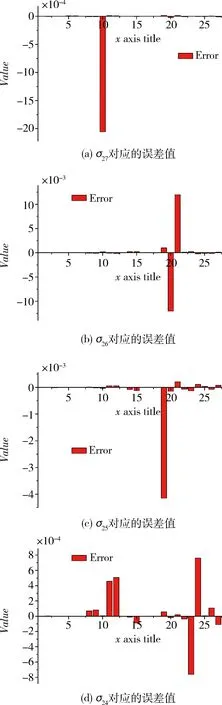
图3 奇异值对应的误差系数值

利用仿真弹道得到遥外差并计算观测矩阵。首先，直接利用最小二乘估计得出27项误差系数估计值，其中前文提及的不可观测项其估计值与真值偏离大，甚至完全不可信。然后，去掉完全不可观测的误差项，将线性相关项合并后重新计算，其估计值更接近真值，整体估值效果得到明显改善，验证了前文可观测性结论的正确性。表2为前文得出的12项不可观测误差项估值与真值的对比。表中陀螺仪误差系数单位为(°)/h，表中误差项的单位均为1.0×10-5。

同时，图3(d)中σ24=0.55905对应的误差项有第11，12，23和24项，即该4项误差的观测矩阵相关性极强，其中既有加速度计误差又有陀螺误差项，即加速度计误差与陀螺误差耦合紧密，前文只对加速度计误差、陀螺误差分别进行简单合并，没有考虑加速度计与陀螺的耦合关系，加之最小二乘法在处理复共线性较强的问题时有很大的局限性，估计值与真值仍有较大偏差，可以考虑应用贝叶斯估计、主成分估计等算法改进估值效果。

表2 误差项真值与估计值对比

5 结论

在捷联系统工具误差可观测性分析过程中，分别计算观测矩阵的奇异值对应的误差项的值，可具体分析每一项误差的可观测性，对应的奇异值越小，则该项误差系数的可观测性越差；且同一项奇异值对应的误差项具有线性相关关系，可为误差项的取舍、合并提供依据。

[1] David H T-itterton,Jhon L Weston.Strapdown Inertial Navigation Technology[M]. 2nd ed. UnitedKingdom: The Institution of Electrical Engineers,2004:29-33.

[2] 柴卫华,杜亚东,张树侠.捷联惯导系统可观测性的研究[J].哈尔滨工程大学学报, 2000，21(2)：10-14.(Chai Weihua,Du Yadong,Zhang Shuxia.The Study of Observability of Strapdown Inertial Navigation System[J].Journal of Harbin Engineering University, 2000,21(2):10-14.)

[3] 徐延万.弹道导弹、运载火箭控制系统设计与分析[M].北京: 宇航出版社, 1999.

[4] 程向红，万德钧，仲巡.捷联惯导系统的可观测性和可观测度研究[J].东南大学学报，1997，27(6)：6-10.(Cheng Xianghong,Wan Dejun,Zhong Xun.Study on Observability and Its Degree of Strapdown Inertial Navigation System[J].Journal of Southeast University,1997, 27(6)：6-10.)

[5] 吴俊伟，孙国伟，张如，等.基于SVD方法的INS传递对准的可观测性能分析[J].中国惯性技术学报，2005，13(6)：26-30.(Wu Junwei,Sun Guowei,Zhang Ru，et al.Analysis on Observability of INS Transfer Alignment Based on SVD Method[J].Journal of Chinese Inertial Technology, 2005,13(6):26-30.)

The Observability Analysis of SINS Instrumental Error Based on Observation Equations

GAO Yeye LI Huabin LI Ling SONG Weijun

Beijing Aerospace Automatic Control Institute, Beijing 100854, China

RegardingtheproblemofSINSerrorobservation,establisharelativelycompletelaserSIMUmodelisestablishedandtheformulasofSINSobservationequationarederivedininertialreferenceframe.Then, SVDisusedtostudytheobservationoftheinstrumentalerror.Finally,atrajectorysimulationisusedasaninstancetodemonstratetheSINSerrorobservabilityandfeatures.

SINS;Instrumentalerror;Observation; SVD

2014-01-15

高叶叶(1989-)，女，河北保定人，硕士研究生，主要研究方向为导航与制导；李华滨(1966-)，男，广西蒙山县人，研究员，主要研究方向为飞行器导航、制导与控制；李 伶(1972-)，女，湖北赤壁人，研究员，主要研究方向为飞行器制导与控制；宋维军(1979-)，男，山东日照人，高级工程师，主要研究方向为飞行器导航、制导与控制。

V249.32+2

A

1006-3242(2014)03-0029-04