Weitzenbock不等式的一个有趣隔离猜想的解决
2014-08-09 03:35
中学教研(数学) 2014年4期
●
(广雅中学 广东广州 510160)

当且仅当△ABC为等边三角形时,等号成立.文献[1]从新的角度给出它的一个有趣隔离如下:
定理1[1]在△ABC中,设a,b,c分别为BC,CA,AB的边长,相应于顶点A,B,C的中线长为ma,mb,mc,内角平分线长为wa,wb,wc,高线长分别为ha,hb,hc,△ABC的面积记为S,则
当且仅当△ABC为等边三角形时,等号成立.
进而提出如下猜想:
猜想[1]在△ABC中,设a,b,c分别为BC,CA,AB的边长,相应于顶点A,B,C的中线长为ma,mb,mc,内角平分线长为wa,wb,wc,高线长分别为ha,hb,hc,△ABC面积记为S,则
当且仅当△ABC为等边三角形时,等号成立.
经探讨发现,左边不等式不成立,中间和右边不等式成立.
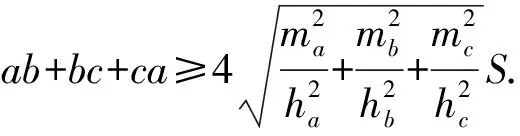
在△ABC中,取a=b=5,c=2,则
ab+bc+ca=5×5+5×2+2×5=45,
下证中间不等式成立,为此,将其加强为
定理2在△ABC中,设a,b,c,s分别为BC,CA,AB的边长和半周长,相应于顶点A,B,C的内角平分线长为wa,wb,wc,高线长分别为ha,hb,hc,△ABC的面积记为S,则
当且仅当△ABC为等边三角形时,等号成立.

(ab+bc+ca)2≥a2(a+b+c)(b+c-a)+b2(a+b+c)(c+a-b)+c2(a+b+c)(a+b-c)
⟺a4+b4+c4-a2b2-b2c2-c2a2≥0⟺2a4+2b4+2c4-2a2b2-2b2c2-2c2a2≥0
⟺(a2-b2)2+(b2-c2)2+(c2-a2)2≥0.
参 考 文 献
[1] 秦庆雄,范花妹.Weitzenbock不等式的一个有趣隔离[J].中学教研(数学),2014(1):41-42.
猜你喜欢
中学生数理化·七年级数学人教版(2021年9期)2021-11-20
中学生数理化·七年级数学人教版(2020年9期)2020-11-16
中学生数理化·七年级数学人教版(2019年9期)2019-11-16
中学数学杂志(初中版)(2019年6期)2019-01-14
学生天地·小学低年级版(2018年9期)2018-12-03
——书写要点(三)
学生天地(2018年33期)2018-11-08
学生天地·小学低年级版(2018年11期)2018-01-05
中学生数理化·七年级数学人教版(2017年2期)2017-03-25
科技创新导报(2016年24期)2017-03-13
浙江共产党员(2017年4期)2017-01-24

