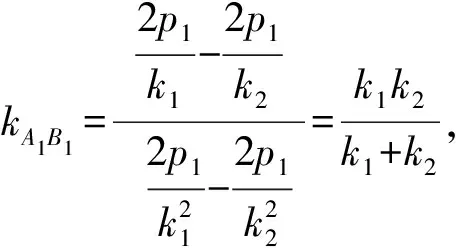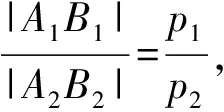有关相似抛物线性质的探究

●

(德清县第三中学 浙江德清 313201)

最近，笔者在翻阅文献[1]和文献[2]时，发现他们都对相似椭圆的性质作了一些探究，得到了一些优美的性质.著名数学家波利亚说过：当你找到第一个蘑菇或做出第一个发现后，再四处看看，它们总是成群生长的.考虑到圆锥曲线之间往往有相似的性质，文献[1]、[2]中的性质对双曲线的情形都是成立的，受其启发，笔者得到了有关相似抛物线的3组整齐而优美的性质，现将结论叙述如下：

性质已知相似抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0)，p1

(1)A1B1∥A2B2,A1C1∥A2C2,B1C1∥B2C2,A1F1∥A2F2,B1F1∥B2F2,C1F1∥C2F2;

证明设直线l1：y=k1x，直线l2:y=k2x，则

所以kA1B1=kA2B2，即A1B1∥A2B2.

由于直线B1C1,B2C2分别是过点B1,B2的切线，故

得kB1C1=kB2C2，即B1C1∥B2C2,

同理可证

A1C1∥A2C2.

因为

所以kB1F1=kB2F2，即B1F1∥B2F2,

同理可证

A1F1∥A2F2.

由于A1B1∥A2B2,A1C1∥A2C2,B1C1∥B2C2,故△A1B1C1∽△A2B2C2，即

于是

所以

得

由于B1C1∥B2C2且B1F1∥B2F2，故

∠C1B1F1=∠C2B2F2，∠OF1B1=∠OF2B2,

△B1C1F1∽△B2C2F2,

得

∠C1F1B1=∠C2F2B2,

因此∠OF1C1= ∠OF1B1+∠C1F1B1=

∠OF2B2+∠C2F2B2=∠OF2C2，

得

C1F1∥C2F2.

综合上述，A1B1∥A2B2,A1C1∥A2C2,B1C1∥B2C2,A1F1∥A2F2,B1F1∥B2F2,C1F1∥C2F2.

从而

再由B1F1∥B2F2,B1C1∥B2C2,C1F1∥C2F2，知△B1F1C1∽△B2F2C2，故

从而

同理可得

△A1F1C1∽△A2F2C2，

故

从而

同理可得

△A1F1B1∽△A2F2B2，

故

综合上述,

(3)由第(2)小题知

评注利用斜率公式，通过直线之间的斜率相等来证明直线的平行，又利用相似三角形的性质来证明线段和三角形面积的比例关系，体现了通性通法的思想.证明过程整齐划一，给人以“一气呵成”之感，体现出数学的简洁美和整齐美.

结束语笔者通过类比探究的数学思想方法，得到了一些整齐、优美的性质，体会到了数学结论的简洁美和和谐美，有助于提高我们对数学结论的欣赏和鉴别能力，体会数学结论的整齐、漂亮，给人以一种美的享受.同时，通过上面的探究过程，有助于我们更加深刻地理解数学(初等数学)，有助于提高教学科研意识.上述这种探究过程，正印证了著名数学家波利亚的一句话：没有任何一个题目是彻底完成了的，总还会有些事情可以做；在经过充分的研究和观察以后，我们可以将任何解题方法加以改进；而且无论如何，我们总可以深化对答案的理解.

参 考 文 献

[1] 姚源.相似椭圆系的若干性质[J].中学教研(数学)，2013(10):48-49.

[2] 姜坤崇.相似椭圆性质又探[J].数学通讯:下半月，2011(4):36-37.