以三角形为背景的高考试题归类解析

●

(马寅初中学 浙江嵊州 312400)

●施哲明

(嵊州市教研室 浙江嵊州 312400)

三角形是最简单的封闭几何图形．从小学、初中到高中，数学学习与三角形的联系越来越紧密和频繁，在数学的各种学习内容、各类试题背景中成为最活跃的几何图形之一．这个小小的三角形中充满了无限的奥秘和变化：从最基本的3条线段、3个角的组成来看就包含着许多优美的性质，既有边长关系，又有角度关系，还有边角合一的正弦定理、余弦定理等等；若涉及中线、角平分线、垂线等，那更是到了一个神奇的三角王国；若再把它隐藏到某一些几何图形中，如圆锥曲线中的特征三角形、立体几何中的线面角和面面角等，那更显得丰富多彩，真可以说是三角、代数、几何、图形的百川交汇．正由于它在平凡中充满着无穷的魅力，因此得到高考命题者的青睐．本文例举若干以三角形为背景的试题，展现它在试题命制中的不同侧面，供大家欣赏和参考．

1 定理为先，“边角”互通

在高中数学中，三角形性质的代数化表达中，最重要的就是正弦定理和余弦定理，它们沟通了三角形的边角关系，也提供了边角相互转化的工具．因此高考中有关三角形的试题最直接、最常见的就是应用正弦定理、余弦定理解决三角形中的有关度量问题．

(1)求A；

(2012年新课标全国数学高考试题第17题)

分析(1)由已知条件及正弦定理得

因为B=π-A-C，所以

得

评析正弦定理和余弦定理是解决有关斜三角形边角问题的2个重要定理，利用这2个定理可将边角关系达到统一．本题第(1)小题求角，故需把边转化为角；第(2)小题求边长，故需选用含3个边长变量的余弦定理．在研究较复杂的三角形问题时，常需正、余弦定理综合使用，甚至反复使用．

2 向量为“桥”，运算为“梁”

从向量进入高中数学后，三角形的几何性质就可以用向量的形式来表现．既具代数表达形式又具非凡魅力的几何意义的向量，在解决许多以三角形为背景的高考试题中，成为一道亮丽的风景线．

A．2 B．4 C．5 D．10

(2012年江西省数学高考试题第7题)

分析1以C为原点、CA，CB所在直线为x，y轴建立直角坐标系.设A(a,0)，B(0,b),则

从而 |PA|2+ |PB|2=

故选D．

故选D．

分析3由平行四边形性质得

故选D．

评析此题以直角三角形为背景呈现，初看似乎与平面向量无关，但倘若运用代数方法来解决此题会觉得无从入手，但一旦看清此题考查的真正意图，再合理运用平面向量的运算，就能迎刃而解．真所谓是“不识庐山真面目，只缘身在此山中”．

( )

A．∠ABC=90° B．∠BAC=90°

C．AB=ACD．AC=BC

(2013年浙江省数学高考理科试题第7题)

图1

分析如图1，在△ABC中，设BC的中点为D，则

同理可得

3 多“管”齐下，精彩纷呈

在高中数学中，涉及到三角形性质的试题，其表现形式往往是代数形态.而解决的主要手段，也是借助于三角、代数的方法．但在实际问题中，我们常常结合几何图形采用多种方法，从不同角度加以解决，这也恰好反映了三角形在高中数学中的魅力所在．

例4在△ABC中，AB=4，M为BC的中点，且AM=1，则∠BAC的最小值为______．

(2013～2014学年第一学期浙江省嵊州市高三期末检测试题)

解法1(以所求∠BAC为目标)如图2，由余弦定理得

a2=16+b2-8bcos∠BAC,

(1)

由式(2)，式(3)得

a2=4-16bcos∠BAC,

(4)

由式(1)，式(4)得

故∠BAC≥150°．

图2 图3

解法2(以所求角的补角∠ABD为目标)如图3，延长AM到点D，使得AM=MD，联结BD,CD.设∠ABD=θ，BD=x，则由余弦定理得

4=16+x2-8xcosθ，

即

故θ≤30°，从而∠BAC≥150°．

解法3在△ABD中，由正弦定理得

即

图4

(x+6)2+y2=4，

这就是点C的轨迹．当AC与圆相切的时候，∠BAC的最小值为150°．

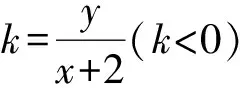
故∠BAC的最小值为150°．

解法6如图5，延长BA到点Q，使得BA=AQ.因为点M为BC的中点，所以AM为QC的中位线，从而QC=2，即点C的轨迹是以Q为圆心、半径为2的圆．故当AC与圆Q相切时，∠BAC的最小值为150°．

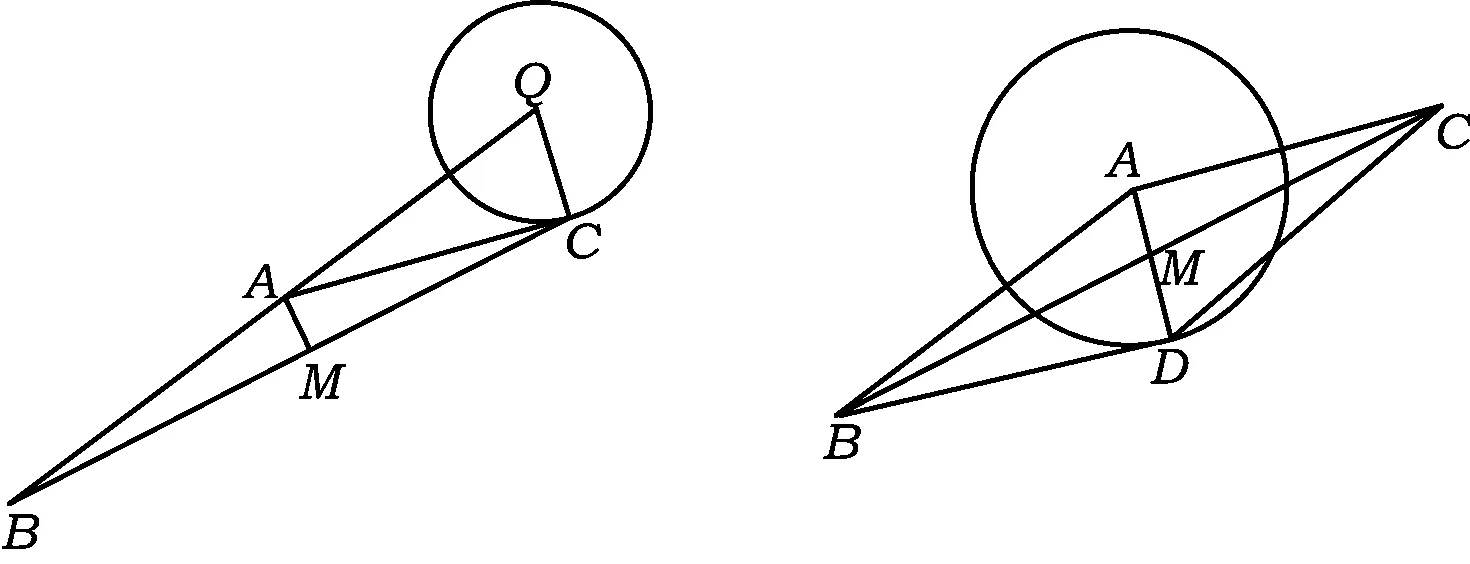
图5 图6

解法7(以中点M的轨迹为目标)如图6，延长AM到点D，使得AM=MD.因为AD=2，所以点D在以A为圆心、半径为2的圆上，当BD与圆相切时，∠ABD最大，从而∠BAC的最小值为150°．

评析运用三角、向量的代数运算和几何运算、解析几何、数形结合等多种数学方法，紧紧围绕解题目标，展开了不同的解法，充分展示了三角形命题在高中数学中的复杂性和解法的多样性、综合性.本题无论从试题的命制，还是解法的呈现，都让人赏心悦目，余味无穷．

4 置之于“形”，百花齐放

正如前面所述，三角形是最简单也是最基本的平面封闭图形,许多试题往往将它“镶嵌”于其中，并以它作为背景、有机地融合了各方面的知识进行考查，形成了一批内涵丰富、立意新颖的试题．

( )

A．{Sn}为递减数列

B．{Sn}为递增数列

C．{S2n-1}为递增数列，{S2n}为递减数列

D．{S2n-1}为递减数列，{S2n}为递增数列

(2013年全国数学高考试题第12题)

分析通过边长的递推关系，得

结合an+1=an，可知点An在以Bn，Cn为焦点的椭圆上，且

故边BnCn上的高逐渐增大.又因为|BnCn|=a1，所以{Sn}为递增数列．

评析此题将三角形的顶点以递推数列的动态形式给出，隐含圆锥曲线定义于其中，也不是通过简单的高的变化来反映三角形的面积，而是通过相邻2条边的长度之间的关系来体现三角形的面积变化.在领略不凡新意的同时，对学生的逻辑思维能力和数学想象能力给予了深度的考查．

(2013年浙江省金华市高三月考试题第16题)

图7

分析如图7，依题意有

|BF1|= |AF1|-|AB|=

|AF1|-|AF2|=2a.

因为|BF2|-|BF1|=2a，所以

|BF2|=4a，

故

|AF2|=4a,|AF1|=6a.

又∠F1AF2=60°,|F1F2|=2c,由余弦定理得

4c2=36a2+16a2-2×6a×4a×cos60°=28a2，

随着学习阶段的提升，有关三角形的试题的变化，表现特征为从几何图形及几何性质向代数形式转变，从单一的知识向综合性知识转变，从简单背景向复杂背景转变．这就需要教师在教学中，抓住三角形几何性质的不同表现形式，综合运用各种方法，灵活应用几何结论，方能简捷高效地解决新形式的三角形问题．