相似于Jordan块的矩阵A的所有变换矩阵

蔡 吟， 王丽庆

(温州大学 数学与信息科学学院，浙江 温州 325035)

北京大学数学系所著的“高等代数”[1]和李炯生的“线性代数”[2]都已经证明：对任意非零矩阵A，存在可逆矩阵Q，使得Q-1AQ=J，其中J是A的Jordan标准型，并且这样的Q不唯一.而在张贤科的“高等代数学”中给出了如何求出一个非零矩阵Jordan标准化的变换矩阵的方法，但是没有说明如何求解所有的变换矩阵.事实上，对于一个一般的非零矩阵来说，要找到它Jordan标准化所对应的所有变换矩阵是复杂而困难的.此处主要探究与n阶Jordan块相似的矩阵，其Jordan标准化时所对应的变换矩阵的全体.

1 所有变换矩阵的探究和证明

首先“Q是矩阵A的Jordan化的变换矩阵”的一个必要条件[3]：

设Q=(α1，α2，…，αn)，且λ为A的特征值.由Q-1AQ=J可知， AQ=QJ，即(A-λE)Q=Q(J-λE)，化简即有AQ=QJ的一个等价条件：

(A-λE)j-1α1=αj(j=2，3，…，n)，(A-λE)nα1=0

定义1 分别设

通过公式αij=(A-λE)j-1αi1即可得到n组不同的αi2，αi3，…，αin，从而得到n 个不同的Pi=(αi1，αi2，…，αin)(i=1，2，…，n).定义这n个不同的Pi为A的基础矩阵(显然Pi满足APi=PiJ的等价条件，即满足APi=PiJ).

定理1 Pi的第j列(即αij)和(A-λE)j-1的第i列相等(j=2，3，…，n).

证明

(1)

比较左右两个矩阵的每一列，即可得原命题得证.

另外不难发现

αin=(A-λE)n-1αi1=Q(J-λE)n-1Q-1αi1

令

当αin=(≠)0时，

也就是说b1i=0当且仅当αin为零向量.

定理2 基础矩阵Pi可逆当且仅当Pi的最后一列不为零向量(αin≠0).

证明当αin=0时，Pi显然不可逆；当αin≠0时，如果能证明k1αi1+…+knαin=0成立，当且仅当k1=k2=…=kn=0时成立，那么Pi为可逆矩阵即可得证.

″⟸″：显然成立.

″⟹″：0=Q-10=Q-1(k1αi1+k2αi2+…+knαin)=

Q-1(k1QQ-1αi1+k2Q(J-λE)Q-1αi1+…+knQ(J-λE)n-1Q-1αi1)=

于是得到方程组

0=k1b1i

(2)

0=k2b1i+k1b2i

(3)

0=knb1i+kn-1b2i+…+k1bni

(4)

结合式(2)与b1i≠0，可得k1=0，再结合式(3)又可得k2=0，综上，即可得k1=k2=…=kn=0，从而原命题得证.

推论1 W为A的基础矩阵的线性组合时，W可逆当且仅当W的最后一列不为零向量.此命题的证明可以直接从定理4的证明过程中得出.

定理3 任给一个n阶非零矩阵W，都存在且唯一存在n个常数t1，t2，…，tn和非零n阶矩阵H(其中H的第一列为零向量)，使得W=t1P1+t2P2+…+tnPn+H成立.

证明设W的第一列为(c1，c2，…，cn)T，显然W=t1P1+t2P2+…+tnPn+H当且仅当ti=ci(i=1，2，…，n)，H=W-(t1P1+t2P2+…+tnPn).

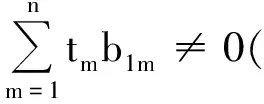
证明当W不为A的基础矩阵的线性组合时，存在n个常数t1，t2，…，tn和非零n阶矩阵H(其中H的第一列为零向量)，使得W=t1P1+t2P2+…+tnPn+H成立.

由于H的第一列为零向量，且H为非零矩阵，因此AH-HJ≠0，即W必然不是A的Jordan化的变换矩阵.

当W为A的基础矩阵的线性组合，即W=t1P1+t2P2+…+tnPn时，

因此，W为A的Jordan化的变换矩阵当且仅当W可逆.下面讨论W的可逆性.

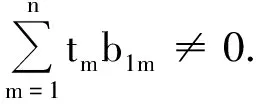
综上所述，原命题得证.

结合推论1和定理4，又可得出定理4的另一个等价命题(定理5).

定理5 W为A(其中A相似于Jordan块矩阵)的Jordan化的变换矩阵当且仅当W为A的基础矩阵的线性组合，且W的最后一列不为零向量.

2 例 题

例题1 求A的Jordan化的所有变换矩阵，其中

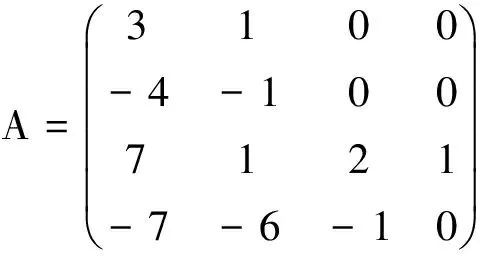
解A的Jordan标准型

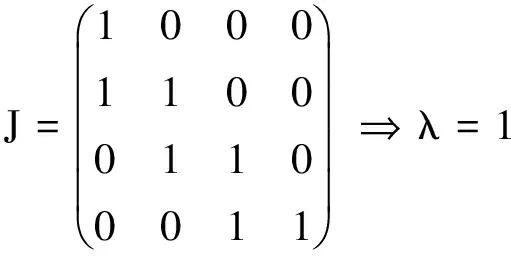
而

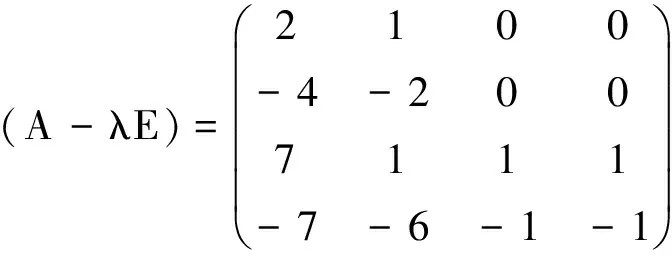
于是

另外任取一个变换矩阵的逆

于是得所有变换矩阵

其中，t1，t2，t3，t4满足2t1+t2≠0.

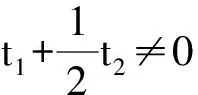
例题2 求A的Jordan化的所有变换矩阵，其中

解A的Jordan标准型

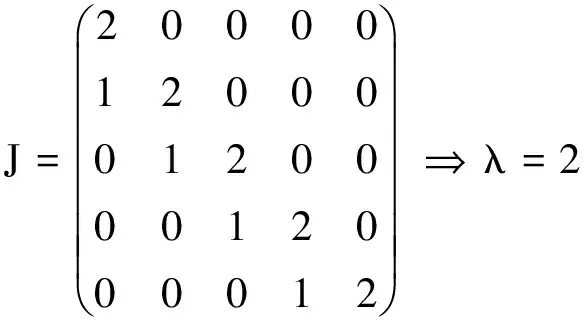
而

于是

另外任取一个变换矩阵的逆

于是得所有的变换矩阵

W=t1P1+t2P2+t3P3+t4P4+t5P5=

其中，t1，t2，t3，t4，t5满足t1-t2≠0.

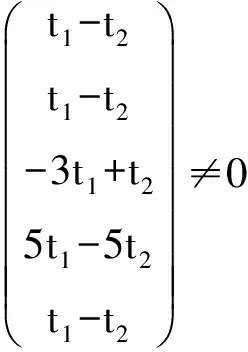
参考文献：

[1] 北京大学数学系几何与代数教研室代数小组.高等代数[M].3版.北京：高等教育出版社，2003

[2] 李炯生，查建国.线性代数[M]. 2版.安徽：中国科学技术大学出版社，2003

[3] 张贤科，许甫华.高等代数学[M].2版.北京：清华大学出版社，2008