基于粒子群优化的LS-SVM短期风电功率预测研究*
王 静, 林 森, 孙 仙, 张 羽, 唐 静
(1. 巢湖学院 电子工程与电气自动化学院,安徽 巢湖,238000 ;2. 国网安徽无为县供电有限责任公司,安徽 芜湖,241000;)
随着能源危机的加剧,逐步优化能源结构、提高能源效率、发展可再生能源已经成为我国可持续发展战略中的不可缺少的重要组成部分.风力发电作为一种可再生能源,对环境无害或危害极小,而且资源分布广泛,适宜就地开发利用,已经在世界各国得到广泛关注.我国幅员辽阔,海岸线长,风能资源比较丰富,仅陆地上的风能储量就有约3亿kW,加上近岸海域可利用的风能资源,共约计10亿kW,具有相当大的开发潜力.虽然我国的风电开发起步晚,技术水平较低,但历经20多年的发展和不断自主创新,总装机容量已达130万kW.风电具有随机性、间歇性和波动性等弊端,所以风电并网功率超过一定值之后,会严重影响电能质量和电力系统的运行,降低电网运行安全系数,并给电力部门的预测调度带来困难.因此,对风电功率较准确的预测,可以调整调度计划,有效减轻风电对整个电网的不利影响[1].目前,预测的方法很多,如回归分析法、人工神经网络、灰色预测模型法、组合预测法等,方法均有各自适用范围,但在解决小样本、非线性、局部极小点等问题上还存在不足.调用2013年全国电工杯数学建模大赛的实际数据,采用基于粒子群优化的LS-SVM进行短期风电功率预测,以进一步提高预测精度和运算速度.
1 LS-SVM和粒子群算法原理
1.1 支持向量机
支持向量机(Support Vector Machine,SVM)最早是由Vapnik等人在20世纪60年代提出的,用以解决分类和回归问题,并以其出色的自学习特性成功应用于很多领域.它的原理是将输入向量通过非线性映射φ(·)映射到高维特征空间H里,将经验风险最小化转化成结构风险最小化,利用结构风险最小化原则构造最优决策函数,最后运用原低维空间的核函数替代H中的点积运算,用线性的方法解决非线性问题,从而在空间H中构造最优回归函数用以解决原空间里的回归问题,最优回归函数表达式:
f(x)=w·φ(x)+c
(1)
表达式中w——权值向量,w∈Rk;c——常数,c∈R.
SVM的成功地运用最优化方法解决机器学习问题,克服了过学习和维数灾等传统学习的缺陷.
1.2 最小二乘支持向量机(LS-SVM)
最小二乘支持向量机(Least Squares Support Vector Machines, LS-SVM)是由Suykens等人提出的一种新型SVM方法,它继承了SVM的基本思想,是SVM的一种扩展和变形,在分类和回归问题中的基本原理和SVM类似.其回归原理如下:
给定训练样本集D={(xk,yk)|k=1,2,…,N},其中xk∈Rn为输入数据,yk∈R为输出数据.在权w空间中的函数估计问题可以转化成求解以下问题[2]:
其中,φ(·)是映射函数;误差变量ek∈R;b是偏差量;γ是可调超参数.由式(2)可定义拉格朗日函数:
(4)
其中:拉格朗日乘子ak∈R.对式(4)进行优化,即求L对w,b,ek,ak的偏导数等于0,消除变量w,e.同时,根据Mercer条件,即存在映射函数φ(·)以及核函数满足:
ψ(xk,xl)=φ(xk)·φ(xl)
(5)
最小二乘支持向量机的回归函数表达式为
(6)
1.3 粒子群算法原理

图1 PSO原理流程图
粒子群算法(ParticleSwarmOptimization,PSO),来源于对鸟类捕食行为的研究,是一种基于群体和适应度的具有全局寻优能力的优化算法.最早在1995年由美国电器工程师RussellEberhart和社会心理学家JamesKennedy共同提出.它通过粒子间的相互作用,对解空间进行智能搜索,从而发现最优解.PSO算法流程如下:
(1) 初始化所有个体信息:首先初始化每个粒子的位置信息和速度信息, 将个体的历史最优位置设为当前位置,群体中的当前历史最优个体则设为的;
(2) 确定每个粒子的适应度;
(3) 由矢量来决定在解空间中运动的粒子的运动方向以及位移,一般来说,粒子会跟随现存的最优粒子而动,并且逐代搜索直至获得最优解;
(4) 在每一代中,粒子将跟踪两个极值,第一个就是粒子本身所找到的最优解,这个解称为局部最优值.另一个极值是整个种群目前找到的最优解,称为全局最优值[2,6].PSO原理流程见图1.
优化工具的优点在于操作简单,收敛速度快,有很多措施可以避免陷入局部最优,可调参数少,并且对于参数的选择已经有成熟的理论研究成果,因此在工程应用中比较广.
2 粒子群优化最小二乘支持向量机模型
2.1 参数选取
在LS-SVM的设计中,一项重要内容就是选择最优的核函数和核参数,因为核函数是替代高维空间点积运算的关键,Vapnik研究发现不同核函数对LS-SVM影响甚微,而核参数、惩罚参数C才是影响仿真结果的源头[4].
选择高斯RBF核函数ψ(xi,xj)为LS-SVM核函数.
ψ(xi,xj)=φ(xi)·φ(xj)
(7)
即
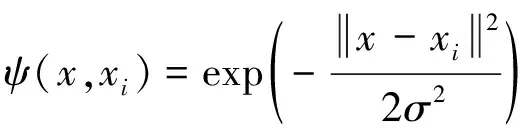
(8)
测试均方误差(MSE)如式(9)
(9)
在LS-SVM 中,可调参数有两个,即超参数γ与核参数σ2,γ对应向量机中的惩罚因子C,其作用是决定训练误差的大小和泛化能力的强弱;σ2反映了训练样本数据的分布和范围特征[3].
2.2 优化建模
参数的选取会直接影响支持向量机预测的精度,传统方法是通过人工不断调试更改参数值来确立最优模型,这种方式效果不佳.选取PSO算法对LS-SVM的参数进行搜索,以得到最优参数,构建最优模型.具体优化建模步骤如下[4]:
(1) 粒子群初始化,设定迭代次数、群体数量,待优化向量由超参数和核参数组成;
(2) 将初始化的粒子群代入LS-SVM进行训练,产生的均方差折算成适应值,计算每个粒子的适应值;
(3) 参照适应值更新最优位置和最优解;
(4) 更新粒子的速度和位置;
(5) 若满足条件,则终止训练并输出最优解;否则转(2).
3 实例分析
对数据的处理,采用式(10),将有量纲的量转化成无量纲量,作用是将数据映射到区间[0,1],加快训练网络的收敛速度[5].
(10)
粒子群算法的参数设置:种群规模L=20,c1=c2=1.43,最大迭代次数t=100,ω=1.14.
3.1 PSO优化LS-SVM预测分析
根据上述优化模型,采用2013年全国电工杯数学建模大赛的实际风功率数据进行仿真.采用每15 min为一个点,将一天分为96个点,对应96个功率数据,选取2006-05-10至2006-05-25日期间机组P输出功率为训练样本,2006-05-26至2006-05-30日为测试样本,预测2006-05-31日96个时间点的功率数据.仿真结果如图2、3.

图3 预测结果对比
图2中,PSO-LS-SVM模型的最佳适应度曲线和平均适应度曲线虽然个别点差值比较大,但也在0.04,绝大部分差值在0.1,因此适应度能够符合要求.图3中,粒子群优化的模型得出的仿真曲线与真实值曲线已经相差甚微,足以说明优化后的模型在很大程度上符合预测要求.
3.2 PSO-LS-SVM模型仿真对比
PSO-LS-SVM模型与未优化的LS-SVM以及RBF模型进行对比,如图3、4,优化之后的模型比LS-SVM以及RBF模型更加接近目标曲线.并且从误差对比曲线可以看出,PSO-LS-SVM模型的误差较其他两个模型波动很小,且误差值也很小,总是在0上下波动,各种误差值对比如表1.由此可知优化后模型的有效性.

图4 3种模型误差对比
表1风功率预测模型统计
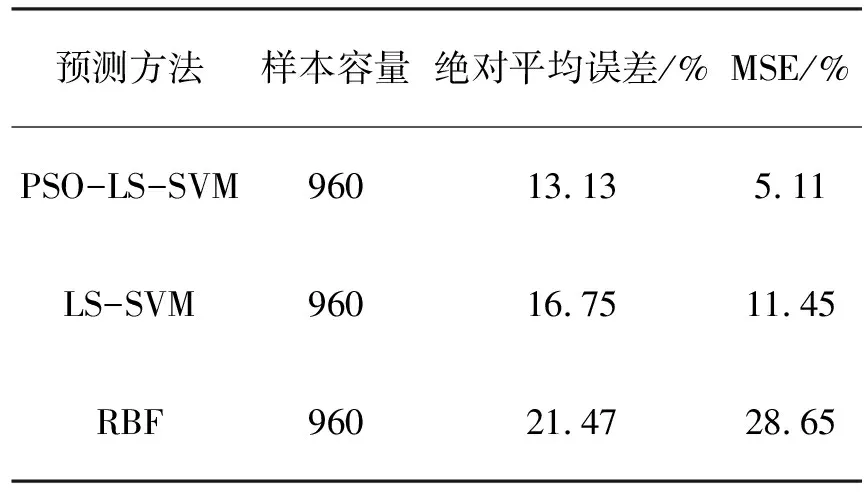
预测方法样本容量绝对平均误差/%MSE/%PSO-LS-SVM96013.135.11LS-SVM96016.7511.45RBF96021.4728.65
4 结束语
建立了基于粒子群优化的LS-SVM预测模型(PSO-LS-SVM),利用粒子群算法对寻找LS-SVM的最优参数,然后进行仿真.将模型应用到风功率预测中,并将预测的结果和误差同LS-SVM以及RBF模型进行对比,结果验证了模型具有训练时间短、精度高等优点,在风功率预测中的颇具有效性和可行性.
参考文献:
[1] 杜祥琬. 中国可再生能源发展战略研究丛书:风能卷[M]. 北京: 中国电力出版社, 2008
[2] 李文元,闫海华,姚宏杰. 粒子群优化的最小二乘支持向量机在通信装备故障预测中的应用[J]. 微电子学与计算机:2013,30(2):99-102
[3] 叶徐静. 基于最小二乘支持向量机的风电功率超短期预测[J]. 电源学报:2013(2):30-35
[4] JONGLAK P,ISSARACHAI N. A heuristic training-based least squares supportvector machines for power system stabilization by SMES[J]. Expert Systems with Applications,2011,38(11): 13 987-13 993
[5] SANCHO S S,EMILIO G O. Short term wind speed prediction based on evolutionary support vector regression algorithms[J]. Expert Systems with Applications, 2011,38(4): 4 052-4 057
[6] 范高锋,王伟胜,刘纯,等. 基于人工神经网络的风电功率预测[J]. 中国电机工程学报: 2008,28: 118-123

