求解非线性互补问题的非单调算法*

侯春莉， 王宣战

(1. 淄博师范高等专科学校 数理科学系，山东省 淄博市 255130；2. 中国石油大学(华东) 理学院，山东省 青岛市 266580)

0 引 言

标准的非线性互补问题(Nonlinear Complementarity Problem，简称NCP)就是求一个向量x*∈Rn使得

x*≥0，F(x*)≥0，〈x*，F(x*)〉=0

其中F是Rn到自身的一个映射，〈·，·〉表示Rn中的内积. 当S为Rn的非负卦限时，VIP(VariationalInequalityProblems)和NCP是完全等价的.VIP和NCP是应用数学中的一个十分重要的研究领域，在数学规划、力学、工程、经济、交通等许多领域有广泛的应用[1，2].此处将利用非线性互补问题的价值函数，结合Gu.N.Z.[3]的非单调搜索技术提出新的求解非线性互补问题的非单调下降算法，该算法中的Gu.N.Z.的非单调技术继承了Grippo[4]，ZhangH.C.[5]非单调技术优点,同时避免了M，ηk，Qk参数选取，进一步增大了搜索步长，减少了迭代次数，加快了算法收敛；并在F(x)为强单调时，证明了算法的全局收敛性；用数值例子验证算法的有效性.

1 算 法

Solodov在文献[6]中提出的价值函数引起人们的极大兴趣，它将NCP等价转化为一个带有简单非负约束的优化问题. 文献[6]的价值函数定义如式(1)：

(1)

其中xi和Fi(x)分别表示向量x和F(x)的第i个分量，ψ：R2→R，

(2)

由文献[6]可以将非线性互补问题(NCP)等价转化为一个带有非负约束的最优化问题

minΨ(x)

s.t.x≥0

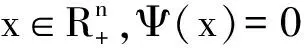
由式(1)(2)给出价值函数Ψ(x)的梯度

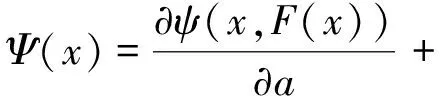
定义

(3)

其中X=diag(x1，x2，...，xn).下面由引理1说明d是一个可行方向，进一步由引理2说明d是一个下降方向.

引理1 设xk≥0是算法(NCPNMDA)产生的第k个迭代点，xk+1是算法(NCPNMDA)产生的第k+1个迭代点，由算法(NCPNMDA)知，λk为迭代步长，dk是由式(5)定义的.如果

则有xk+1=xk+λkdk≥0.

证明对于每一个分量

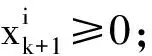
下面，假定映射F在Rn上是强单调的，即∃μ>0，使得

〈F(x)-F(y)，x-y〉≥μ‖x-y‖2， ∀x，y∈Rn

引理2 假设F(x)是连续可微的且是模为μ强单调的，则dk是价值函数Ψ(x)在xk处的一个下降方向，即▽Ψ(x)Td≤0.

证明由F(x)是模为μ强单调的，即

〈F(x)-F(y)，x-y〉≥μ‖x-y‖2，∀x，y∈Rn

则有

〈▽F(x)y，y〉≥μ‖y‖2

(4)

由xi∈R+和Fi(x)∈R，再由式(2)有

因此

(5)

故由式(4)(5)得

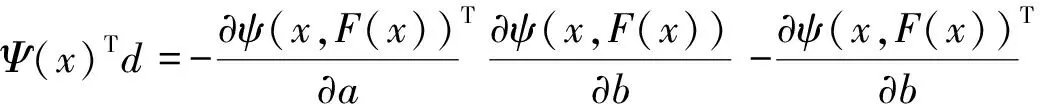
-μ‖d‖2≤0

(6)

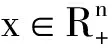
下面给出新的非单调下降算法(NCPNMDA)的具体步骤：

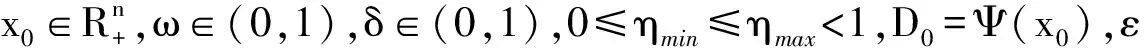
Step1 若Ψ(xk)=0或者Ψ(xk)<ε，则停，即xk是非线性互补问题的一个解，否则转Step2；

Step2 由式(3)知

(7)

转Step3；

Step3 mk是满足式(8)的最小非负整数

Ψ(xk+ωkmkdk)≤Dk+δωkmk〈▽Ψ(xk)，dk〉

(8)

其中ωk=min{ω，tk}，令λk=ωmk，转Step4；

Step4 xk+1=xk+λkdk，转Step5；

Step5 给出满足某种规则的ηk∈[ηmin，ηmax]，计算

Dk+1=ηkDk+(1-ηk)Ψ(xk+1)

(9)

k：=k+1，转Step1.

注：当η=0时，该算法(NCPNMDA)就退化为单调下降算法，记为NCPMDA.

2 收敛性分析

引理3 {xk}是算法(NCPNMDA)产生的无穷序列，则有

(i) Ψ(xk+1)≤Dk，∀k；

(ii) Ψ(xk)≤Dk，∀k.

证明由式(6)(8)知

Ψ(xk+1)≤Dk+δλk〈▽Ψ(xk)，dk〉≤Dk-μ‖dk‖2

(10)

因此，Ψ(xk+1)≤Dk，∀k.

由式(9)(10)知

Dk+1=ηkDk+(1-ηk)Ψ(xk+1)≥ηkΨ(xk+1)+(1-ηk)Ψ(xk+1)=Ψ(xk+1)

又由D0=Ψ(x0)知

Ψ(xk)≤Dk，∀k

证毕.

引理4 {xk}是由算法(NCPNMDA)产生的无穷序列，则{Dk}单调不增且有界.

证明由算法(NCPNMDA)的构造和引理3的(i)知

Dk+1=ηkDk+(1-ηk)Ψ(xk+1)≤ηkDk+(1-ηk)Dk=Dk

再由Ψ(xk)≥0和引理3的(ii)知{Dk}单调不增且有界. 证毕.

定理1[7]假设F是模为μ强单调的，则水平

是有界的.

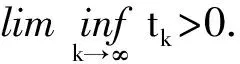
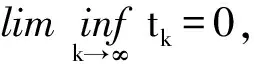
记子列为{xkj}，则‖F(xkj)‖→∞，又由F是连续的，有

‖xkj‖→∞，kj→∞

(11)

则式(11)与定理1结论xk有界矛盾，故结论得证.证毕.

定理2 假设F(x)是连续可微的且是模为μ强单调的，{xk}是由算法(NCPNMDA)产生的无穷序列，则{xk}的任一聚点是NCP的一个解.

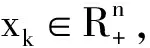
由算法(NCPNMDA)的构造和式(7)(8)得

即Dk+1-Dk≤(1-ηk)(δλk〈▽Ψ(xk)，dk〉).

由引理2知

Dk+1-Dk≤-(1-ηk)μδλk‖dk‖2

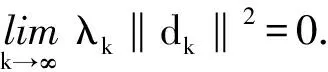
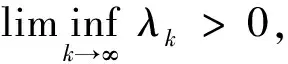
由搜索规则知，对∀k∈N0，有

Ψ(xk+ω-1λkdk)-Ψ(xk)≥Ψ(xk+ω-1λkdk)-Dk>δω-1λk〈▽Ψ(xk)，dk〉

利用中值定理有

〈▽Ψ(ξk)，dk〉>δ〈▽Ψ(xk)，dk〉

(12)

其中，ξk=xk+θkω-1λkdk，θk∈(0，1).

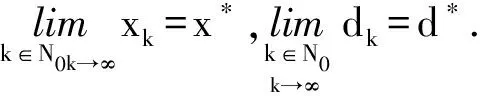
由式(12)得

〈▽Ψ(x*)，d*〉>δ〈▽Ψ(x*)，d*〉

(13)

由式(6)得

〈▽Ψ(x*)，d*〉≤-μ‖d*‖2

(14)

由式(13)(14)得‖d*‖=0，即由文献[6]引理2.1知，x*是NCP的一个解.证毕.

由定理2和文献[8]可以得到推论1.

推论1 假设F：Rn→Rn是连续可微且强单调的，则NCP有唯一解.

3 数值试验

运用MATLAB语言对本节算法编写程序，在ThinkPadT430电脑上对参考文献[6][8]中的数值例子进行数值试验，同时与单调步长的算法进行比较.

记本章算法为算法NCPNMDA，单调线搜索下降算法为算法NCPMDA，并将这两个算法的数值结果进行比较.取ω=0.5，δ=0.85，η=0.3，ε<10-5，从任意大于0的初始点开始，来验证算法的有效性.用x表示初始值，用n表示初始点的维数，用k表示算法的迭代次数.两个例子的F都是在Rn上强单调的，对应的NCP有唯一解.在数值结果中，迭代次数是指主算法的迭代次数.

例1 设F(x)=Mx+q，其中

表1给出了不同维数n和不同初始点x的数值结果，图1给出了计算分析图.

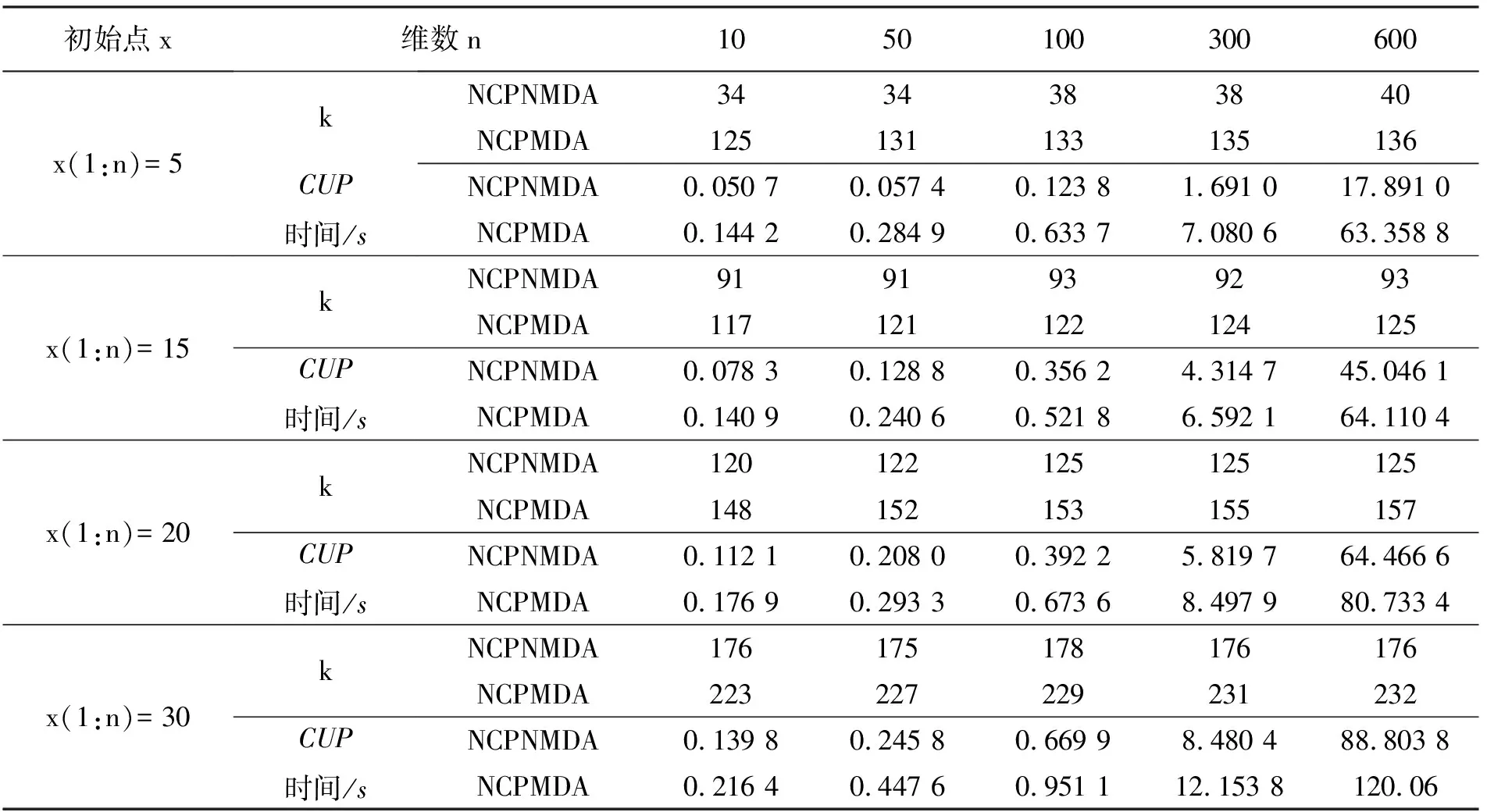
表1 例1的计算结果

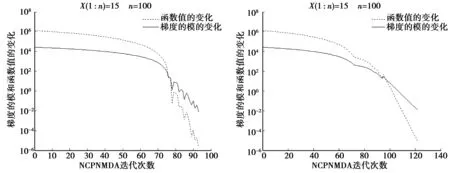
图1 例1的计算分析图

例2 设F(x)=Mx+q，其中

表2给出了不同维数n和不同初始点x的数值结果，图2给出了计算分析图.

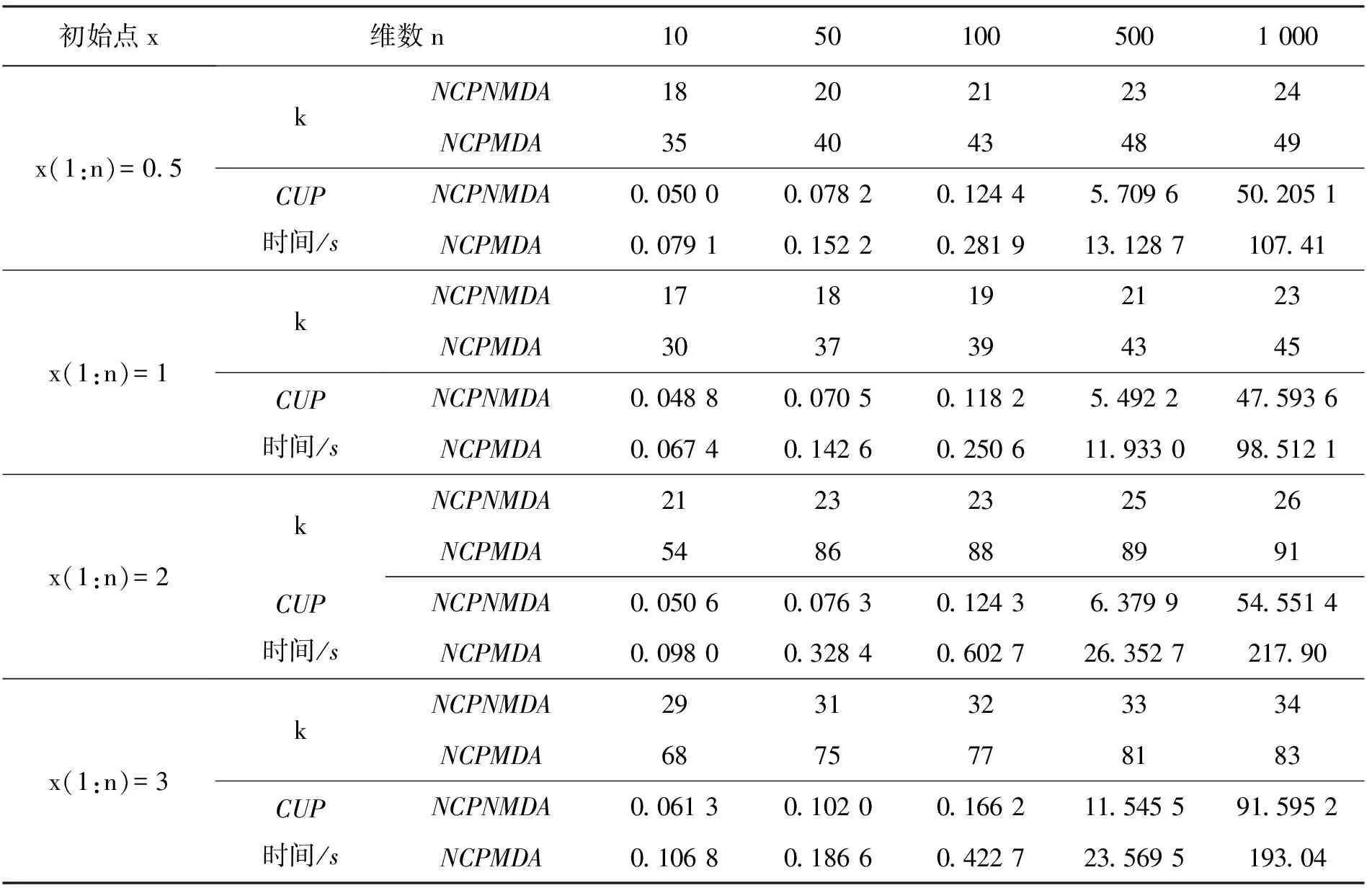
表2 例2的计算结果

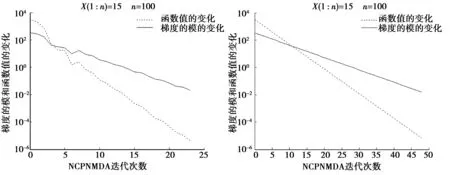
图2 例2的计算分析图

通过上述数值例子的计算结果可以看出，从低维到高维，再到初始点的取值，新算法(NCPNMDA)都能快速有效地求得最优解，并且具有良好的稳定性；无论从迭代次数还是运行时间都远远少于单调算法(NCPMDA).因此，新算法(NCPNMDA)是有效的，适合求解中大规模问题.

参考文献：

[1] TANG J Y， DONG L. A New Class of Non-monotone Memory Gradient Method and Its Global Convergence[J]. Mathematical Theory and Applications， 2009， 29(2)：5-8

[2] 乌彩英，陈国庆. 大规模非线性互补问题的共轭梯度法[J]. 数学的实践与认识，2012，42(3)：185-193

[3] GU N Z， MO J T. Incorporating Nonmonotone Strategies Into the Trust Region Method for Unconstrained Optimization[J]. Computers & Mathematics with Applications， 2008， 55(9)：2158-2172

[4] GRIPPO L， LAMPARIELLO F， LUCIDI S. A Nonmonotone Line Search Technique for Newton’s Method [J]. SIAM Journal on Numerical Analysis，1986， 23(4)：707-716

[5] ZHANG H C， HAGER W W. A Non-monotone Line Search Technique and Its Application to Unconstrained Optimization [J]. SIAM Journal on Optimization， 2004， 14(4)：1043-1056

[6] SOLODOV M V. Stationary Points of Bounded Constrained Minimization Reformulations of Complementarity Problems [J]. Journal of Optimization Theory and Applications， 1997， 94(2)：449-467

[7] WANG Y J， WANG C Y. A Descent Algorithm for Solving Nonlinear Complementarity Problem[J]. Or Transactions， 2004(5)：60-66

[8] GEIGER C， KANZOW C. On the Resolution of Monotone Complementarity Problems [J]. Computational Optimization and Applications， 1996， 2(5)：155-173