Sharp增广拉格朗日函数的局部鞍点
张 斐 婓
(重庆师范大学 数学学院,重庆 401331)
考虑非线性规划问题:
(P) minf(x)
s.t.g(x)=0
x∈X
其中X⊆Rn为非空闭集,函数f:Rn→R, g:Rn→Rm,g(x)=(g1(x),…,gm(x))均二次连续可微,记R+,‖·‖,〈·,·〉分别表示非负实数集、欧几里得范数及Rn上的欧氏内积.
1 研究背景
原始-对偶方法是解决约束非线性规划问题的一种重要方法,但非凸情形下,原问题和对偶问题的最优解可能不相等,即存在非零对偶间隙[1,2].克服这一缺陷的重要途径,便是增广拉格朗日方法,如文献[3],[4]和[5]就在一定的条件下证明了零对偶性间隙等价于增广拉格朗日函数鞍点的存在性.受此启发,此处研究了在二阶充分性条件下sharp增广拉格朗日函数的局部鞍点的存在性.
定义1 问题(P)的增广拉格朗日函数为L:Rn×Rm×R+→R;L(x,λ,c)=f(x)+c‖g(x)‖+〈λ,g(x)〉,其中x∈Rn,λ∈Rm,c∈R+.
定义2 对某个c>0,(x*,λ*)称为L的局部鞍点,当且仅当∃δ>0,使L(x*,λ,c)≤L(x*,λ*,c)≤L(x,λ*,c)对∀(x,λ,c)∈X∩N(x*,δ)×Rm×R+成立,N(x*,δ)为x*的邻域.
2 局部鞍点与局部最优解之间的关系
定理1 ∀x*∈X存在λ*∈Rm及c>0使(x*,λ*)为L的局部鞍点,则x*为(P)的局部最优解.
证明因为(x*,λ*,c)是(P)的局部鞍点,即
L(x*,λ,c)≤L(x*,λ*,c)
(1)
L(x*,λ,c)≤L(x,λ*,c)
(2)
由式(1),f(x*)+c‖g(x*)‖+〈λ,g(x*)〉≤f(x*)+c‖g(x*)‖+〈λ*,g(x*)〉.即〈λ,g(x*)〉≤〈λ*,g(x*)〉对一切λ∈Rm均成立.
若∃i0∈{1,2,…,m},使|gi0(x*)|≠0,有
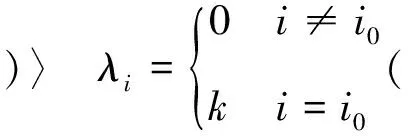
(3)
或
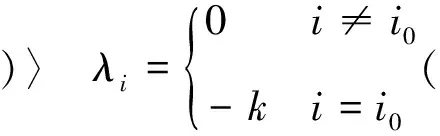
(4)
令k→∞,式(3)(4)左端为+∞,矛盾,所以x*为(P)的可行点.
由式(2),当x为(P)的可行点时,L(x*,λ*,c)=f(x*)≤L(x,λ*,c)=f(x),所以x*是(P)的局部极小点.
3 二阶充分性条件
设x*是问题(P)的一个可行点,
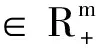
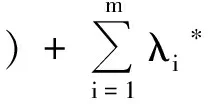
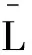

f(x*)>L(xk,λ*,k)=f(x*)+k‖g(xk)‖+〈λ*,g(xk)〉
即


o(‖xk-x*‖2)+k‖▽g(x*)T(xk-x*)+o(‖xk-x*‖)‖+
(5)

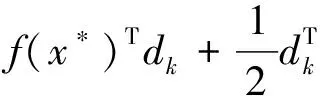
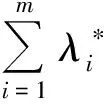
(6)
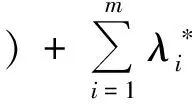
4 结束语
对非线性规划问题(P),研究了sharp增广拉格朗日函数在二阶充分性条件下鞍点的存在性,为应用原始-对偶方法创造了条件.
参考文献:
[1] 袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997
[2] XU Z K.Local Saddle Points and Convexification for Nonconvex Optimization Problems[J]. J Optim Theory Appl,1997 (94):739-746
[3] WU H X,LUO H Z. Saddle Points of General Augmented Lagrangians for Constrained Nonconvex Optimization[J].J Glob Optim,2012(53):683-697
[4] LIU Q,TANG W M,YANG X M.Properties of Saddle Points for Generalized Augmented Lagrangian[J].Math Meth Oper Res ,2009(69):111-124
[5] REGINA S. BURACHIK, RAFAIL N,et al.On a Modified Subgradient Algorithm for Dual Problems Via Sharp Augmented Lagrangian[J]. Journal of Global Optimization, 2006 (34):55-78

