基于改进DV-Hop算法的无线传感器网络定位研究*

李 鹏

(长江大学 计算机科学学院，湖北 荆州 434023)

0 引 言

无线传感器网络是由部署在监测区域内大量的具有计算和通信能力的微型传感器节点组成，通过无线通信的方式形成一个多跳的自组织的网络系统[1]，其作用是利用传感器来监测、收集、处理信息数据，传感器的无线收发装置将数据通过无线通信传输。传感器节点的定位是无线传感器网络的基本功能。根据是否需要测量实际节点间的距离，把无线传感器网络定位算法分为两类：基于距离的定位算法(Range-based)和距离无关的定位算法(Range-free)[2]。基于距离的定位算法共同特点是需要测量相邻节点间的绝对距离或方位，并通过测量的绝对距离和方位来计算未知节点的位置；距离无关的定位算法则不需要测量节点间的绝对距离或方位，而是要得到节点间的估计距离，然后利用估计距离计算节点位置。

距离无关的定位算法通常有DV-Hop算法、质心算法、APIT算法等经典算法[3]。其中DV-Hop算法使用每跳平均距离乘以跳段数来计算节点间距离，对网络节点的硬件设备要求低，部署简单，实现起来比较简易，缺点是节点间的跳段距离是估算出来的，用节点间的跳段距离代替节点间的实际直线距离是不精确的，存在误差[4]。在分析了传统DV-Hop算法特点的基础上，提出了一种改进的DV-Hop算法，主要思想是利用粒子群优化算法对DV-Hop算法中的每跳平均距离误差函数进行优化，从而精确了节点间的跳段距离，达到了对DV-Hop算法校正的目的，通过三边测量法计算出的未知节点的位置更精确。

1 无线传感器网络定位技术

1.1 定位技术基本概念

在传感器网络节点定位中，节点分为信标节点和未知节点，信标节点是未知节点的参考点，信标节点数量比未知节点要少，信标节点可通过GPS定位装置来确定自己的准确位置，而未知节点通过和邻近的信标节点或者是已经确定位置的未知节点进行通信，来确定自己的位置。

1.2 测量节点位置基本方法

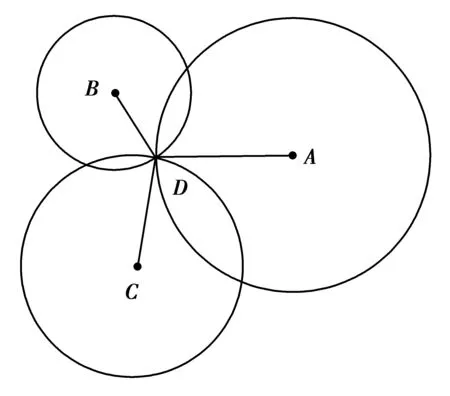
图1 三边测量法图示

计算节点位置的方法有三边测量法、三角测量法、极大似然估计法。在此主要介绍三边测量法[5]，三边测量法是未知节点接收到3个以上信标节点的位置信息后(以3个信标节点为例)，就可以得到未知节点到3个信标节点的距离，然后可以算出未知节点的坐标，三边测量法图示如图1所示。假设已知3个信标节点A、B、C的坐标分别为(xA，yA)、(xB，yB)、(xC，yC)，未知节点的坐标为(x，y)，未知节点到3个信标节点的距离分别为dA，dB，dC，则：

(1)

通过式(1)可得到未知节点D的坐标为

(2)

1.3 定位性能评价标准

无线传感器网络定位系统算法很多，常用的衡量定位能力的标准有定位精度，定位精度是指定位系统提供的位置信息的精确程度，是评价定位能力的最关键的标准，精度越高，技术要求也越高。除此之外，还有覆盖范围、信标节点密度、节点密度、容错性和鲁棒性以及功耗等。

2 定位算法分析

2.1 基于距离的定位算法

基于距离的定位机制(Range-based)分为3个阶段：第1阶段为测距阶段；第2阶段为定位阶段；第3阶段是修正阶段，对第2阶段计算得到的未知节点的坐标精确化，减少误差。基于距离的定位算法通常有：基于接收信号强度指示算法RSSI、到达时间方法TOA、到达时间差方法TDOA、到达角度方法AOA等。

2.2 距离无关的定位算法

基于距离的定位算法可以精确定位未知节点的坐标，但是对无线传感器节点的硬件要求很高，导致无线传感器节点的硬件开销大、能耗高，因此人们提出了距离无关的定位技术。距离无关的定位技术不需要测量节点间的绝对距离或角度信息，只需网络连通性等约束来实现节点的定位，降低了无线传感器节点的硬件开销，但定位误差会相应的增加。距离无关的定位算法通常有质心算法、DV-Hop算法、APIT算法等经典算法，在此主要介绍DV-Hop算法。DV-Hop算法(距离向量-跳段)[6]定位过程如下：

首先，计算未知节点与每个信标节点之间的最小跳段数量，网络中信标节点通过距离矢量交换协议发送一个广播分组，将该信标节点的位置信息和跳数广播到整个网络，广播分组包括该信标节点号、坐标位置(xi，yi)，以及跳数，跳数初始化为0。当节点接收到该信标节点的广播分组后对比自己的数据表的跳数和该分组的跳数，如果该分组跳数小于本节点数据表内的跳数，则用分组的跳数代替节点的跳数，将跳数加1，并且广播该分组，如果该分组的跳数大于本节点数据表内的跳数，则丢弃该分组，而且不广播该分组。这样，所有的未知节点都能获得与所有信标节点之间的最小跳数。

然后，计算未知节点与信标节点的距离。每个信标节点根据记录的其他信标节点的位置信息和跳数，利用式(3)估算出每跳平均距离

(3)

其中，(xi，yi)，(xj，yj)是信标节点i，j的坐标，hj是信标节点i与j(j≠i)之间的跳数。然后信标节点将计算的每跳平均距离广播到网络中，未知节点记录接收到的第一个每跳平均距离，并将分组转发给邻居节点，未知节点接收到每跳平均距离HopSizei后，根据记录的自己与信标节点之间的跳数h，通过HopSizei×h计算未知节点到每个信标节点的跳段距离。

最后，利用三边测量法或极大似然估计法计算未知节点自身位置。未知节点与各信标节点之间的跳段距离可以计算出，再利用三边测量法或极大似然估计法计算节点自身位置坐标。

DV-Hop算法中每跳平均距离是估算出来的，节点间的跳段距离通过每跳平均距离计算得到，所以用节点间的跳段距离代替节点间的实际直线距离是不精确的，存在误差。在近期一些相关研究中，研究者对DV-Hop算法提出了改进，提高了定位精度。本文提出通过粒子群优化算法优化每跳平均距离误差函数，使得未知节点与信标节点之间的跳段距离更加精确，通过三边测量法计算得到的未知节点的位置也更精确，定位效果良好。

3 粒子群优化算法改进DV-Hop算法

粒子群优化(Particle Swarm Optimization， PSO)算法是模拟鸟类捕食行为的群体智能算法，由美国电气工程师Eberhart和社会心理学家Kennedy于1995年提出[7]。粒子群优化算法是一种全局优化算法，源于对鸟群群体运动行为的研究。PSO算法容易实现，要调整的参数少，广泛应用于各种领域。

3.1 粒子群优化算法

粒子群优化算法的数学描述[8]：粒子群算法中每个个体就是一个“粒子”，代表一个潜在的解，在一个D维目标搜索空间中，每个粒子是空间内的一个点，设有n个代表潜在的解的粒子组成一个群，粒子i(i=1，2，…，n)的D维位置矢量zi=(zi1，zi2，…，ziD)，zi的适应值用来衡量粒子位置的优劣，zi当前的适应值由预先设定的适应值函数计算得到，粒子的飞行速度vi=(vi1，vi2，…，viD)，即粒子的移动距离，记pi为粒子迄今为止搜索到的最优位置，pi=(pi1，pi2，…，piD)，记pg为整个粒子群迄今为止搜索到的最优位置，pg=(pg1，pg2，…，pgD)。每次迭代中，粒子根据以下式子更新速度和位置：

(4)

(5)

其中，i=1，2，…，n；d=1，2，…，D，k是迭代次数，r1和r2是[0，1]之间的随机数，用来保持群体的多样性，c1和c2是学习因子，粒子通过不断学习，最后找出pg就是全局最优解。

3.2 粒子群算法改进DV-Hop算法过程

DV-Hop算法通过每跳平均距离乘以未知节点与信标节点间的跳数来计算未知节点到信标节点的距离，这个距离与实际直线距离是有误差的，通过三边测量法得到的坐标也是有误差的，通过粒子群优化算法校正DV-Hop算法中估算得到的每跳平均距离，从而使得未知节点到信标节点间的跳段距离更加精确，然后利用三边测量法得到未知节点的坐标，DV-Hop算法改进过程如下：

(1) 通过信息广播过程计算未知节点与每个信标节点之间的最小跳数h；

(2) 通过粒子群优化算法优化每跳平均距离误差函数，得到优化后的每跳平均距离，计算出未知节点与信标节点的跳段距离d。首先利用式(3)得到已知信标节点间每跳平均距离HopSizei，设未知节点与信标节点间实际每跳平均距离为HopSizer，则误差函数δ=|HopSizer-HopSizei|，利用粒子群优化算法对误差函数进行优化，利用式(4)和式(5)更新粒子的位置和速度，设置适当的适应值，达到迭代的次数停止运算，找出最优解，得到校正后的每跳平均距离HopSizea，然后通过HopSizea×h得到未知节点与信标节点间的跳段距离d；

(3) 通过第二步得到了经过粒子群优化算法校正的跳段距离d，利用三边测量法计算未知节点自身的位置。

4 仿真实验

本文使用Matlab进行仿真实验，设置100 m×100 m的二维仿真环境，采用随机分布信标节点和未知节点的方式，分成固定信标节点数量、改变节点总数和固定节点总数、改变信标节点数量以及改变节点通信半径等3种情况进行仿真实验，通过仿真实验分析定位误差的多少来对比本算法与传统DV-Hop定位算法。

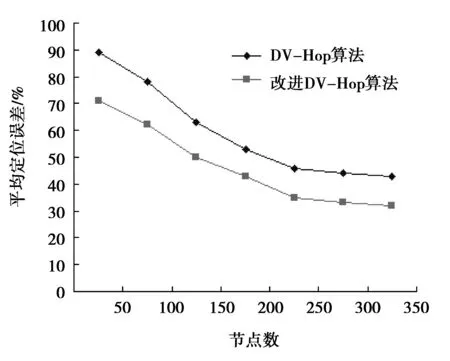
图2 不同节点数的定位误差曲线

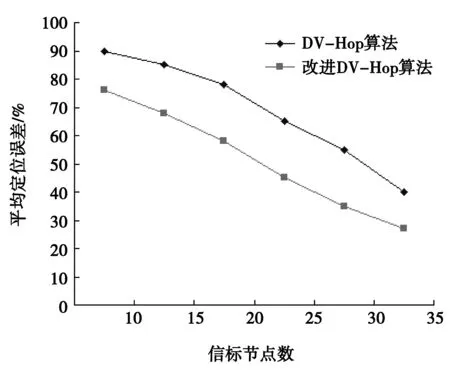
图3 不同信标节点数的定位误差曲线

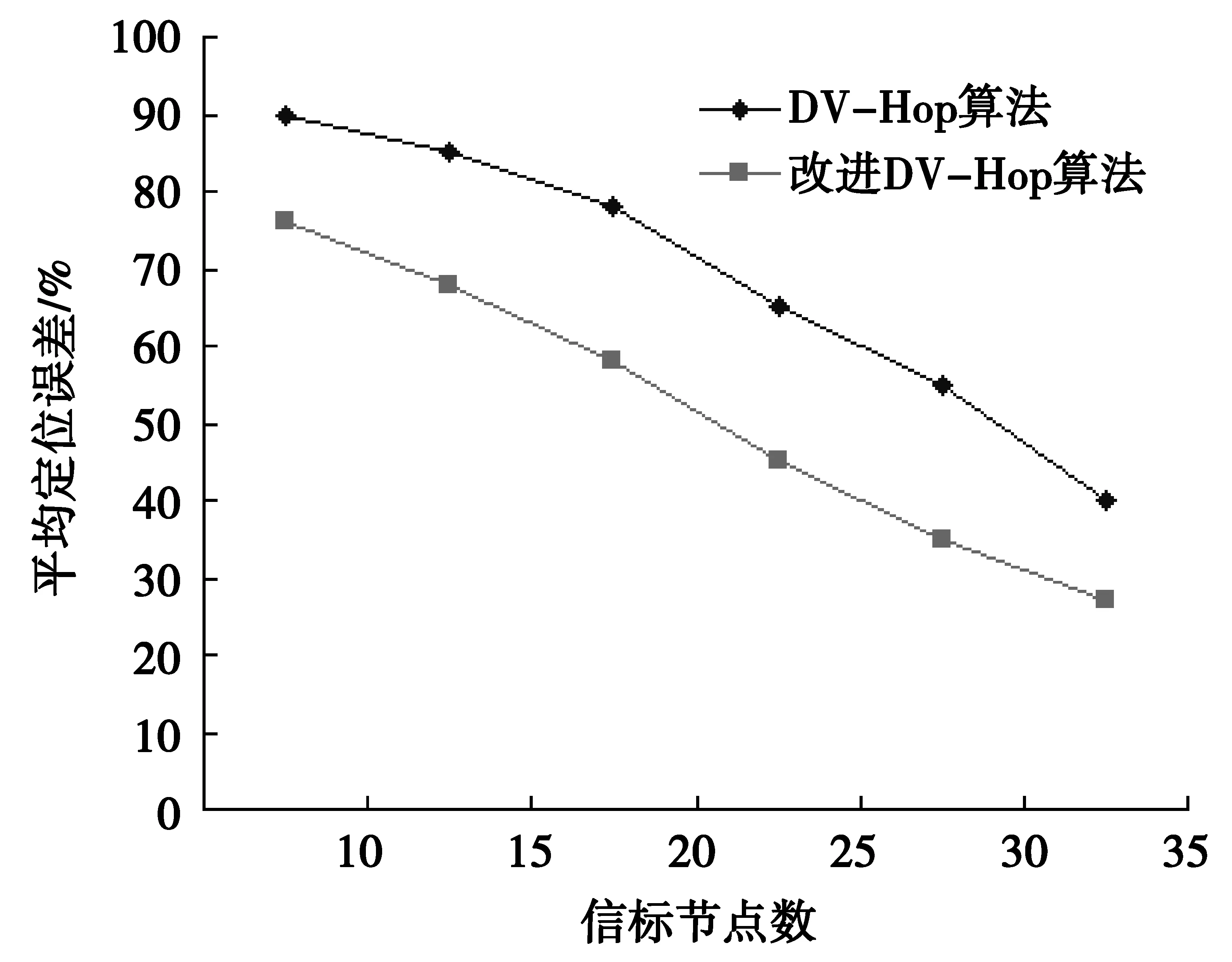
图4 不同节点通信半径的定位误差曲线

(1) 100 m×100 m区域内，设置30个信标节点，节点总数分别为50、100、150、200、250、300、350时仿真情况如图2所示，定位误差随着节点数的增大而下降，通过粒子群优化算法改进的DV-Hop定位算法的定位误差率比传统DV-Hop定位算法的低。

(2) 100 m×100 m区域内，设置节点总数300个，信标节点数量为10、15、20、25、30、35时仿真情况如图3所示，定位误差随着信标节点数的增大而下降，通过粒子群优化算法改进的DV-Hop定位算法的定位误差率比传统DV-Hop定位算法的低。

(3) 100 m×100 m区域内，设置节点总数300个，信标节点占10%，节点通信半径R从10 m到30 m递增，节点通信半径与平均定位误差的关系如图4所示，从图4中可以看出，本文的改进DV-Hop算法优越于传统的DV-Hop算法，当节点的通信半径达到30 m时，平均定位误差下降到20%左右。

5 结束语

DV-Hop算法不需要测量节点间的绝对距离和方位，节点的硬件要求低，开销小，适合大规模布置，受环境因素影响小，适合复杂的监测环境，但是DV-Hop算法定位精度较差，本文采用粒子群优化算法对DV-Hop算法进行了改进，实验表明，提高了定位精度。

参考文献：

[1] 张俊霞， 汪炀， 李善亮. 基于无线传感器网络的定位系统设计[J]. 计算机工程与应用， 2008， 44(17)：67-70

[2] 白凤娥， 姜晓荣， 牟汇慧. 无线传感器网络DV-Hop定位算法的研究[J]. 计算机与数字工程， 2010， 38(3)：34-36

[3] 王汝传， 孙力娟. 无线传感器网络技术及其应用[M]. 北京：人民邮电出版社， 2011：74-76

[4] 孙利民， 李建中， 陈渝，等. 无线传感器网络[M]. 北京：清华大学出版社， 2005：140-142

[5] 彭力. 无线传感器网络技术[M]. 北京：冶金工业出版社， 2011：73-75

[6] 赵灵锴， 洪志全. 基于无线传感器网络的DV-Hop定位算法的改进[J]. 计算机应用， 2011， 31(5)：1189-1192

[7] KENNEDY J， EBERHART R. Particle swarm optimization[C]. Proceedings of the IEEE International Conference on Neural Networks， 1995：1942-1948

[8] 陈星舟， 廖明宏， 林建华. 基于粒子群优化的无线传感器网络节点定位改进[J]. 计算机应用， 2010， 30(7)：1736-1738

[9] 毛会琼， 陈世海， 范建国， 等. 基于无线传感器网络的环境监测系统的设计[J]. 工矿自动化， 2009(8)：119-121

[10] 王晓乐， 徐家品. 基于粒子群优化算法的WSNs节点定位研究[J]. 计算机应用， 2009， 29(02)：494-495