基于局部均值分解和极值差分的直流电机间接测速方法*

雷 钢， 周 铜， 黄传金， 谭联峰

(1. 中州大学 郑州市汽车人机关系与安全重点实验室,河南 郑州 450044；2. 中州大学 科研处,河南 郑州 450044；3. 北京和利时电机技术有限公司,北京 100085)

0 引 言

直流电机换向电流频率含有电机的转速信息，通过分析直流电机起动时电枢电流，可得其起动时的转速特性[1-2]。该方法无需加装转速传感器，特别适用于批量在线测试[3]和转动轴不可见的电机[4]。

早期直流电机的间接测速采用交流放大器对换向脉冲进行放大和整形，然后用数字频率计[5]或单片机系统测出换向脉冲频率[6]，这对硬件要求较高。目前，在电机间接测速领域求取电流频率的方法主要有快速傅里叶变换(Fast Fourier Transform, FFT)[7]、短时傅里叶变换[8]、小波包变换[4,9]、小波脊线算法[10-11]和第二代小波变换[12]。FFT只能获取稳态时的频率特征，无法求取从起动到稳态这一过程中的频率变化；利用小波包良好的时频定位能力不仅能获取稳态时的换向电流频率，也可获取起动过程中的频率，但由于小波包采用离散小波变换，正交分解了时频平面，获取的时频点较少，还要进行曲线拟合，测试精度较低，而且还对分解后的小波包重排，计算量较大[10]；基于小波脊线的电流频率求取方法采用连续小波变换，测试精度较高，但该方法引入了Hilbert变换构造解析函数，将实数领域的频率求解变换到复数领域进行，增加了计算量。短时傅里叶变换、第二代小波变换都受测不准原理限制，很难同时达到时频分析效果。Teager能量算子法[13]、相位差分法[14]也是常用的频率求取方法，但Teager能量算子法仅适用于频率不变的信号；相位差分法包括前向差分、后向差分和中心差分，效果比较好的是中心差分法，其缺点是对噪声太敏感。

近年来，运用Hilbert-Huang变换(HHT)求取多分量信号的频率也是一个研究热点[15]。该方法首先根据经验模态分解(Empirical Mode Decomposition, EMD)将复杂信号自适应地分解为若干固有模态函数(Intrinsic Mode Function, IMF)之和，然后对每个IMF做Hilbert变换从而求其频率。该方法有良好的自适应性，但易出现负频率现象。

局部均值分解(Local Mean Decomposition, LMD)是另外一种根据信号固有包络特征自适应地分析非线性信号方法[16]。LMD首先将多分量信号分解为若干单分量的乘积函数(Product Function,PF)之和，其中PF由调幅-调频函数组成，通过对余弦形式的调频函数求导可获取PF的瞬时频率。这种求取频率方法完全在实数领域中进行，具有较高的运算速度，但LMD分解中常出现余弦形式的调频函数的幅值超出[-1，1]的现象。

本文首先根据LMD构建了自适应滤波器并提取换向电流，然后与采用EMD提取电枢电流的方法做了对比研究；其次，根据直流电机换向特点，提出了一种基于极值差分的频率求取方法，并与小波脊线、HHT中的Hilbert变换和LMD中的反余弦函数方法求取的瞬时频率做了对比，结果证明了本文所提方法的优越性。

1 基于LMD的滤波原理

1.1 LMD原理[17]

LMD可从复杂信号中按频率递减的顺序自适应地依次分离出若干单分量的乘积函数(PF)，且复杂信号可由PF和剩余的单调函数重构。假设复杂信号为x(t)，则对应的分解步骤为[17]

(1) 设ni为信号x(t)的局部极值点，mi为任意两个相邻的局部极值点的平均值，则有:

mi=(ni+ni+1)/2

(1)

将式(1)中所有相邻的局部均值点mi和mi+1用折线连接起来，然后用滑动平均法对其进行平滑处理，得到局部均值函数m11(t)。

(2) 包络估计值ai为

ai(t)=ni-ni+1/2

(2)

将ai和ai+1连接起来并用滑动平均法进行平滑处理，便可得到包络估计函数a11(t)。

(3) 用x(t)减去局部均值函数m11(t)可得到信号h11(t)，即:

h11(t)=x(t)-m11(t)

(3)

(4)h11(t)除以包络估计函数便得到调频函数s11(t)，即:

s11(t)=h11(t)/a11(t)

(4)

将调频函数s11(t)作为原始信号重复以上过程，可得到s11(t)的包络估计函数a12(t)。假如a12(t)不为1，表明s11(t)不是纯调频函数，则将上述迭代过程重复n次，至s1n(t)为纯调频函数时结束，即s1n(t)的包络估计函数a1(n+1)(t)=1，故有:

(5)

(6)

迭代终止的条件为

(7)

实际应用中，为避免过多分解次数，设一个变动量Δ，可令1-Δ≤a1n(t)≤1+Δ时，迭代终止。

(5) 将全部包络估计函数连乘即可得到包络信号a1(t)，即:

(8)

(6) 将包络函数a1(t)与纯调频函数s1n(t)相乘可得初始信号x(t)的第一个PF分量，即:

PF1(t)=a1(t)×s1n(t)

(9)

(7) 将PF1(t)分量从原始信号中x(t)分离，得到一个新的函数u1(t)，对u1(t)重复上述过程循环k次，当uk(t)为单调函数时分解结束。

(10)

从以上分解过程可知，将所有PF分量以及剩余的单调函数相加可重构出原始信号x(t)，即:

(11)

1.2 应用LMD构建滤波器原理

EMD分解出的IMF分量按频率从高到低的特点排列，据此可构建出自适应的时空滤波器[18]。LMD和EMD类似，大量试验发现LMD分解出的PF分量也按频率从高到低的顺序排列。根据这一特点，应用LMD可构建自适应的滤波器。如去掉最后分离出的PF分量，将其余的PF分量相加，则相当于高通滤波器；去掉最开始分离出的几个PF分量，对其余的PF求和，则相当于低通滤波器；将两头的PF分量去掉，保留中间的PF分量，则相当于带通滤波器。应用LMD构建的自适应滤波器(Adaptive filter， AF)可表示为

(12)

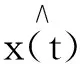
LMD从复杂信号中按频率递减的顺序依次分离出PF分量这一过程实质上是不断从高频滤波到低频滤波的过程，完全体现了多分辨分析自适应的滤波特性。应用LMD构建的滤波器截止频率以及通带都随输入信号不同而改变，这和传统滤波器的固定截止频率具有本质不同。

2 基于极值差分的瞬时频率求取方法

直流电机换向常出现超前换向和延迟换向，换向过程中有可能出现火花或电弧放电现象，且电刷与换向片接触程度、换向器表面的氧化亚铜薄膜所受压力都对换向过程有影响，会造成换向电流波形畸变。用EMD和LMD进行自适应滤波提取换向电流时也很难消除超前换向和延迟换向对换向电流的影响[17-18]。在电流畸变或有毛刺处，直接根据每个采样时刻的相位求取频率会有突变，这时根据所求频率间接获取的转速就和实际不符，因为实际转速一般只能递变不会突变。

根据频率的定义可知相邻波峰或波谷之间的时间间隔是一个周期，周期的倒数可认为是相邻波峰或波谷中间时刻的频率，这种求取频率方法称为基于中心点的极值差分方法。假设ihx(t)为换向电流，则运用极值差分求其频率的步骤如下:

(1) 找出ihx(t)所有的波峰值ihx(τk)，τk为ihx(t)对应的波峰时间，k=1,2,…,N，N为ihx(t)的波峰总数；

(2) 判断第一个波峰值时间是否等于零，如等于零转入(3)；否则，对其进行镜像延拓以解决端点效应，然后进入(3)；

(3) 相邻波峰中点时刻的频率f为

(13)

式中：fs—采样频率。

(4) 检测频率是否存在突变，突变点的频率可用上次求取的频率代替；

(5) 将所求点的频率用最小二乘拟合即可获得换向电流的瞬时频率曲线。

这种通过定位极值点求取频率的方法物理意义明确，最重要的是可有效解决超前换向和延迟换向及可能存在的火花造成的换向电流频率突变问题。

3 间接测速公式和信号采集系统

3.1 间接测速公式

得到普遍认可的直流电机间接测速公式为[4,19]:

(14)

式中:m为换向片数;n为转速;p为电机极对数;c由m的奇偶决定的系数。m为偶数时，c=1 ；m为奇数时，c=2。

3.2 信号采集系统

试验采集系统如图1所示，由永磁直流电动机ZYTD-50SRZ-R、霍尔电流传感器LSTR25N、数据采集卡ARTUSB2850、PC机及直流电源组成。图1中ZYTD-50SRZ-R空载电流为0.18A；空载转速为2000r/min；极对数为1，换向片数为12。由空载转速及电机参数可初步判断换向电流最高频率不超过400Hz，本文选择的采样频率为20kHz，采集的信号如图2所示。从图2及其局部放大图可知，直流电机从暂态起动到稳态运行时电枢电流都含有大量的噪声信号。

图1 直流电动机电枢电流信号采集系统

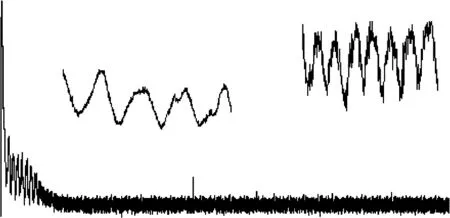
图2 采集的直流电机空载起动时电枢电流信号

4 试验分析结果

对图2所示的电枢电流信号进行LMD分解，得到的系列PF分量如图3所示。为验证LMD的完备性，通过各PF分量和剩余函数重构原始信号。本文对各PF分量和剩余函数求和重构新的电枢电流信号，该信号减去原始的电枢电流信号得到误差信号波形，如图4所示。由图4可知，误差信号的数量级是10-17，由此可知根据各PF分量和剩余信号可重构原始信号，间接证明了LMD分解提取换向电流的可行性。

图3 电枢电流各PF分量和剩余函数

图4 重构信号与原始信号之间的误差曲线

从图3可知，LMD分解电枢电流信号得到的各PF分量依次按频率从高到低的顺序排列。仔细观察图3中的各PF分量可知，PF1和PF2具有幅值小、频率高的特点，可认为是噪声分量；PF3幅值增大，频率降低，可认为其属于换向电流成分；后阶的PF分量频率依次降低，至PF7分量时，其频率近似直流成分，由此可确定式(12)中带通滤波器截止分量的阶数为l=3和h=6，则式(12)中，AF的输出信号即为电枢电流的换向电流，如图5所示。将其与图2对比可知，AF组成的带通滤波器在有效滤除高频的噪声成分和低频的直流分量的同时，较好地保留了换向电流成分。

为对比运用EMD和LMD分析电枢电流的优缺点，根据EMD方法[17]以及LMD方法获取的直流成分如图6(a)所示，二种方法获取的换向电流如图6(b)所示(为便于对比，只显示了换向电流的局部放大图)。从图6(a)可知，EMD提取的直流成分在起动过程中的效果较好，稳态时二种方法提取的直流成分很接近；从图6(b)可知较之EMD方法，LMD提取的换向电流更平滑。另外，本文对比了EMD和LMD分解电机启动电流的计算速度，实验环境为神舟K480P-i5G、Win7和Matlab7.12。EMD采用Rilling提出的“筛分”停止准则[17]，取默认值；LMD的扰动量Δ=0.0001；二者都采用镜像拓延以改善端点效应。得到电枢电流全部IMF分量EMD耗时 2.463026s，而LMD仅运行1.193508s 便分离出全部PF分量。由此可见，LMD的运行速度大大快于EMD，更适合在线测试。究其原因，主要是LMD得到PF分量时采用了除法，而EMD得到IMF分量时采用减法，故LMD的分解速度快于EMD。

图5 运用LMD提取的换向电流

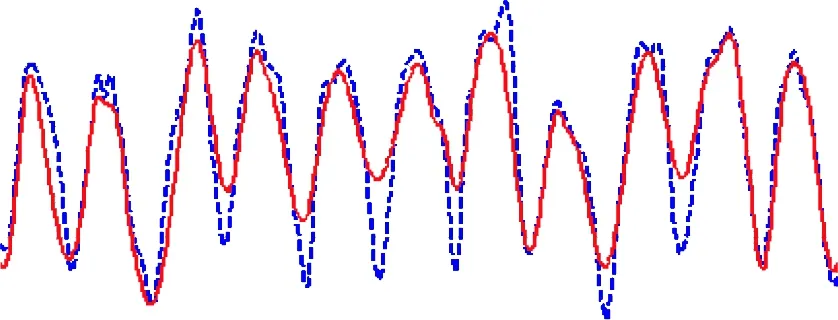
图6 分别运用LMD、EMD获取的直流成分和换向电流

对图6所示的换向电流运用极值差分法求取的频率和小波脊线算法求取的频率(LMD提取的换向电流)如图7所示，其起动电流的傅里叶频谱如图8所示。对比图7、图8可知，运用极值差分法可有效求取EMD和LMD提取的换向电流频率，图7中的三条频率曲线几乎同时进入稳态，这间接验证了采用极值差分求取换向电流频率的正确性。对比图7中运用极值差分求取EMD和LMD提取的换向电流频率可知，LMD提取的换向电流在暂态启动过程中的频率曲线较光滑，且没有突变点。对比极值差分和小波脊线算法求取的瞬时频率曲线发现，小波脊线方法获取的频率曲线在暂态起动过程中的曲线更光滑，但在稳态边界处的波动较大。另外，相对于极值差分，小波脊线算法采用连续小波变换需对每一个采样点进行运算求解，其计算速度较慢，实验中采用cmor6-2型小波进行连续小波变换，尺度为1∶300，求取频率耗时12.633830s，而极值差分方法仅用了0.385791s，可见本文所提算法更适合在线应用。

图9为分别采用HHT中Hilbert变换和LMD中的反余弦函数法求取的换向电流主要模态的频率曲线。从图9可看出运用HHT求取的瞬时频率波动幅度很大，突变点很多。主要原因是换向电流不是规则的正弦波性，由于换向过程的复杂性，换向电流相位会发生畸变，而HHT是通过对瞬时相位求导获取频率曲线，所以其求取直流电机换向电流瞬时频率波动较大；LMD在获取纯调频函数过程中运用滑动平均算法，滑动平均跨度好比窗口滤波，求取的瞬时频率比HHT平滑，但纯调频函数的值常超出[-1，1]范围，所求频率也存在一定程度的波动。

根据式(14)所得转速曲线如图10所示。由闪光测速仪得到的稳态转速为1825r/min，图10中稳态时不同时刻转速在1825r/min附近略有波动，但波动范围很小，在±5r/min之间，直接证明了本文所提方法的可行性。

图7 极值差分和小波脊线求取的瞬时频率

图8 空载起动时的电枢电流傅立叶频谱

图9 采用Hilbert变换和LMD中反余弦法求取的换向电流主要模态的频率曲线

图10 直流电机空载起动时的转速曲线

5 结 语

本文主要做了两个工作，一是构建了基于LMD的自适应滤波器，通过试验对比分析了EMD和LMD在提取直流电机空载起动时换向电流的优缺点；二是提出了基于差分极值算法的换向电流频率求取方法，并与LMD中的反余弦方法、HHT中的Hilbert变换方法和小波脊线等求取频率的算法作了对比。主要结论如下:

(1) 较之EMD方法，LMD提取的换向电流更平滑，并且LMD的分解速度较快，更适合在线应用；

(2) 基于极值差分的频率求取方法可求取换向电流频率；

(3) 对分别采用EMD和LMD提取的换向电流应用极值差分求其频率，LMD方法所对应的换向电流频率在暂态起动过程中的曲线较光滑；

(4) 小波脊线算法求取的暂态频率特性较好，但在稳态边界处波动较大；

(5) 较之小波脊线算法，极值差分的频率求取方法运算速度提高了96.95%，适合在线应用；

(6) LMD中的反余弦方法和Hilbert变换方法不宜直接用于求取换向电流频率。

【参考文献】

[1] 袁宝国，曹镇荣，王胜国.直流电动机反电动势对其电流脉动频率的影响[J].中国电机工程学报，2007，27(30): 92-96.

[2] 袁宝国.换向过程对直流电动机电流脉动频率影响的分析[J].微电机，2007，40(5): 36-38.

[3] 杨琳，崔淑梅，刘曼兰.利用电流脉动测试直流电机转速存在问题的分析[J].微电机，2007，40(4): 82-85.

[4] 黄进，黄建华，陈暾，等.基于小波分析的直流电机转矩-转速特性测试[J].中小型电机，2001，28(2): 49-53.

[5] 张文海.直流电动机的转速测量方法[J].微电机，1996，29(4): 38- 40.

[6] 卢道英，王晓明.微型直流电动机转速测量的一种方法[J].微特电机，1985(3): 31-33.

[7] 袁宝国，周政新，胡志华.直流电动机无传感器测速实验方法[J].微特电机，2007(11): 20-22.

[8] 史敬灼，王岚，徐殿国.基于非平稳信号处理的交流串励电机无传感器测速[J].微电机，2006，39(4): 66-69.

[9] 杨育霞，辛小南，赵亮，等。异步电动机起动特性间接测试的小波方法研究[J].中小型电机，2005，32(4): 59-61.

[10] 牛发亮，黄进.渐进信号瞬时频率提取及其在电机性能测试中的应用[J].电工技术学报，2006，21(4): 122-126.

[11] 宋海军，黄传金，陈铁军，等.基于小波脊线的异步电动机间接测试方法[J].电机与控制应用，2012，39(11): 36-39.

[12] 黄传金，雷刚，陈铁军，等.基于第二代小波的直流电动机间接测速研究[J].微特电机，2013，41(6): 18-21.

[13] MARAGES P， KAISER J F. Energy separation in signal modulation to speech analysis[J]. IEEE Transactions on Signal Process， 1993，41(10): 3024-3051.

[14] 张贤达.非平稳信号分析与处理[M].北京: 国防工业出版社，1998.

[15] HUANG N E， SHEN Z, LONG S R， et al. The empirical mode decomposition and the Hilbert spect-rum for nonlinear and non-stationary time series ana-lysis[J]. Proc Rsoc Lond, 1998(454): 56-78.

[16] SMITH J S. The local mean decomposition and its application to EEG perception data [J]. Journal of The Royal Society Interface, 2005, 2(5): 443- 454.

[17] 黄传金，宋海军，陈铁军，等.微型直流电动机电枢电流提取新方法[J].微特电机，2013，41(4): 10-13.

[18] 黄传金，宋海军，陈铁军，等.基于EMD滤波的直流电动机起动电流高频分量提取方法[J].微特电机，2013，41(5): 28-31.

[19] 胡志华,袁宝国,周政新.直流电动机无传感器测速的一个特例[J].电机与控制应用，2007，34(8): 27-29.