交流伺服电机高性能位置控制的试验研究*

陈 剑, 程国扬

(福州大学 电气工程与自动化学院，福建 福州 350108)

0 引 言

工业伺服系统目前广泛采用永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)这类交流传动装置和基于PID的电流-转速-位置三环串联的控制结构[1-2]。PID控制的瞬态性能对给定输入和扰动的变化缺乏鲁棒性[3]，实际应用中需引入非线性增益[4]、抗饱和等措施[5]。文献[6]利用迭代学习方法对扰动引起的误差进行补偿，速度环仍以PI控制为基础，并缺乏试验验证。文献[7]设计了带有输出误差积分量的增广状态反馈控制律，用于改善PMSM速度跟踪性能，依然存在积分器饱和的风险。文献[8]提出一种基于线性反馈+非线性反馈的复合反馈控制技术，通过非线性反馈来动态改变闭环阻尼，综合了轻阻尼系统的快速响应和重阻尼系统的低超调特性，可实现快速平稳的定点跟踪。文献[8]利用积分来抑制扰动,面临积分器饱和、缺乏性能鲁棒性等潜在问题。

本文针对工业伺服系统的典型需求——快速平稳且准确的点位控制,研究在矢量控制的模式下，把电机的速度和位置环构成的机械子系统作为受控系统，分别以转矩电流和电机转角作为控制输入和受控输出量，借鉴文献[8]的线性+非线性反馈的复合控制结构，在仅有转角可量测(如采用增量式光电编码器)的条件下，设计了一个线性扩展状态观测器来估计系统的转速和未知扰动(包括不确定性和负载转矩等因素)，并用于反馈和补偿，从而实现快速、平稳、准确的位置控制。本文的设计在离散时间域上通过DSP编程实现，并在实际的PMSM上进行了试验验证。

1 PMSM位置伺服系统的模型

本文研究常用的面装式PMSM，其数学模型如下：

(1)

式中：θr——机械转角；

ωr——机械角速度；

Te——电磁转矩；

TL——负载转矩；

J——折合到电机轴上的惯量；

kb——粘性摩擦系数；

Ld、Lq——电机直轴和交轴同步电感；

Rs——定子电阻；

np——极对数；

ψ——永磁体磁链；

ud、uq——dq坐标系中d、q轴的电压；

id、iq——直轴、交轴电流，即励磁电流、转矩电流。

本研究中，电流环的控制沿用常规的PI控制方式，对电机速度和位置环则合在一起作为一个机械子系统进行考虑： 以电机转角θr和转速ωr作为系统的状态变量，其中θr是系统的受控输出量(记为y)，交轴电流iq作为控制输入量u(其值作为转矩电流的给定信号)，可得到如下所示的二阶状态空间模型：

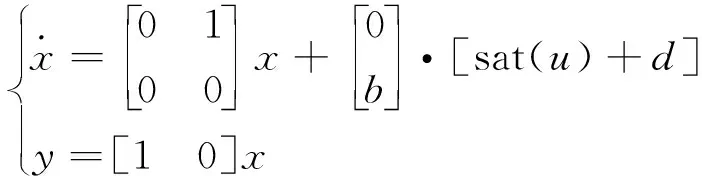
(2)

sat(u)=sign(u)·min{umax,u}

式中： sign(·)是符号函数，umax表示控制量的最大允许值。把式(2)按采样周期T进行基于零阶保持器的离散化，得到如下的离散状态空间模型：

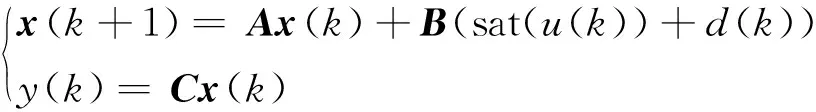
(3)

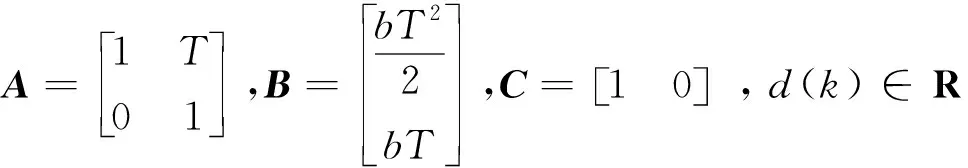
2 离散时间鲁棒非线性控制律

控制目标是使输出y精确地跟踪给定位置r。参照文献[8],首先设计一个带扰动补偿的线性反馈控制律：

uL(k)=Fx(k)+Gr-d(k)

(4)

式中：F是反馈增益矩阵，使(A+BF)具有期望的稳定特征值；G是待定的标量参数。在控制律中，若r和d(k)有界且控制变量未超过其饱和限幅，则系统闭环稳定，且当k→∞,系统的状态量和输出量都将趋于其稳态值，其中输出量的稳态值为

yss=Cxss=C(I-A-BF)-1BGr

由于控制的目标是使输出y能准确跟踪定点目标r，即：yss≡r,∀(r,d)，则有：

C(I-A-BF)-1BG=1

(5)

从式(5)可解得

G=1/[C(I-A-BF)-1B]

(6)

假如选择闭环系统的一对共轭极点的阻尼系数为ζ1,自然频率为ω1，按极点配置方法可得

(7)

式(4)的控制律中需要使用未量测的速度和未知扰动信号，本文把速度和未知扰动一起归入到观测器。根据系统模型(3)的假设条件：d(k+1)=d(k)，即扰动是常值或慢变化的，将其加入系统模型可得到一个增广系统，并设计一个降阶观测器来估计速度和扰动信号：

(8)

其中：λ——观测器内部状态量，λ∈R2；

(9)

式中：e(k)——位置跟踪误差，e(k)=y(k)-r。

为了设计非线性反馈律，选择一个正定对称矩阵W∈R2×2，求解如下Lyapunov方程：

P=(A+BF)TP(A+BF)+W

(10)

得到一个正定矩阵P，此解总是存在的，因为A+BF渐近稳定。则非线性反馈律如下：

(11)

其中Fn=BTP(A+BF)；ρ(e(k))是一个关于误差e(k)的非线性增益函数(非负)，用来逐渐改变闭环极点阻尼系数，以改善系统的跟踪性能。一种可行但不唯一的选择如下：

ρ(e(k))=βarctan(αα0e(k)-1)

(12)

其中：α和β是非负的可调参数。α0与初始误差e(0)相关，用于对误差e(k)进行归一化：

基于观测器(7)，把线性控制律与非线性反馈律合并起来，得到最终的控制律：

(13)

3 试验研究

将提出的控制方法用于一个实际的PMSM位置伺服系统： 电机型号为60CB020C，其额定转速为3000r/min，额定转矩为0.64N·m，极对数为4；带有2500线的光电码盘，利用磁粉制动器来提供负载。电机q轴电流(转矩电流)最大值限定为1.5A,即umax=1.5A。经试验辨识，式(2)中的系统参数为b=1040。采用上一节的控制律对电机位置进行控制，首先选择控制的采样周期为T=0.002s，以及线性反馈的闭环极点参数：ζ1=0.3，ω1=30，计算得到：F=-0.8497 0.0178；选取矩阵W为对角阵diag(0.002,0.002),得到Fn=-0.0518 0.0578；采用式(10)中的增益函数ρ(e(k))，其中参数为β=0.5，α=4；选取观测器极点的阻尼和自然频率为ζ0=0.707,ω0=110，得到如下的观测器方程：

采用TM320F2812DSP作为电机控制的主芯片和磁场定向控制方式。永磁同步电机位置伺服系统结构如图1所示。其中电流环采用带有抗饱和反馈回路的离散PI控制律(采样频率为20kHz)实现闭环控制，电流环的响应时间约为1ms，在设计位置控制环时可忽略电流环的影响。

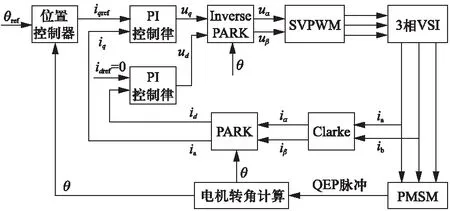
图1 永磁同步电机位置伺服系统结构图

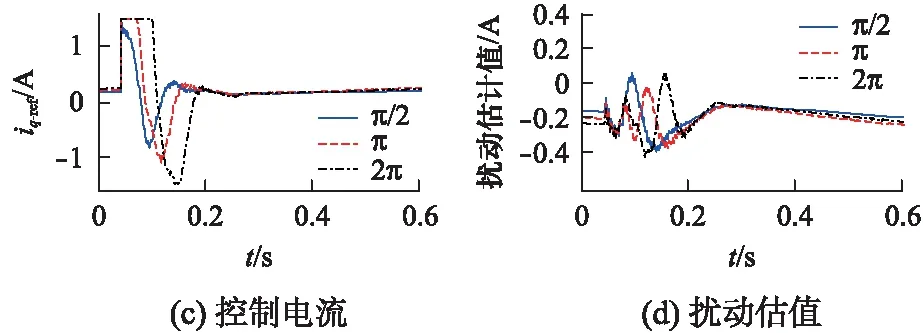
图2 多种目标角位移的试验结果(负载0.12N·m)

图3 目标角位移为π在不同负载下的试验结果

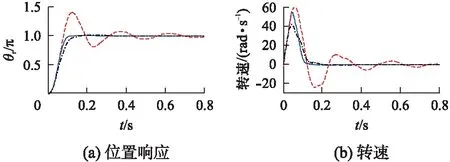
图4 目标位移为π负载0.12N·m不同控制律的试验比较

在Code Composer Studio集成开发环境中进行实时试验，采集的数据转换到MATLAB进行绘图。首先在空载条件下(系统中仍有其他扰动因素)对多种角位移进行了控制试验，结果如图2所示。图2中分别给出了电机位置(归一化处理)、转速、控制电流(转矩电流给定)和扰动估值的波形。由图可知，系统对给定目标能快速且准确地跟踪，最大超调量均在2 %以下，其2 %调节时间分别为0.104、0.98和0.118s。图3给出了角位移为π在多种负载转矩条件下的试验结果。比较可知： 虽然负载扰动的增大使得系统的响应性能有所趋缓，但总体控制效果仍有很好的一致性，扰动补偿对提高系统的稳态精度发挥了有效的作用。图4为目标位移为π负载0.12N·m不同控制律的试验结果。由图可见，该方法的确同时具有轻阻尼系统的快速性与重阻尼系统的低超调特性，实现了快速且平稳的跟踪性能。为考察系统参数发生变化后的控制性能，让控制律中参数b分别取值780和1300(其他可调参数值不变)，在角位移为π和负载0.12N·m(≈20%额定负载)条件下进行定位控制，并与标称情况(b=1040)比较。目标位移为π负载0.12N·m参数摄动后的试验结果如图5所示。由图5可知，系统性能略有恶化，特别是b=1300时超调量稍微超出2 %，但总体控制性能仍在可接受范围内。可见本控制方案对参数变化有一定的鲁棒性。

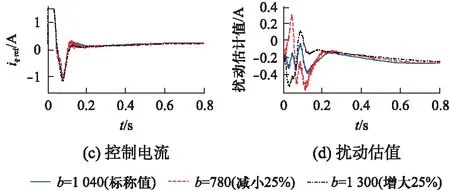
图5 目标位移为π负载0.12N·m参数摄动后的试验结果

4 结 语

本文提出一种在交流伺服电机上实现快速且准确位置控制的离散时间复合控制方案。控制律由线性反馈、非线性反馈、扰动补偿组成。采用降阶扩展状态观测器技术，从电机的位置测量信号中估计出转速和未知负载扰动信号，以实现反馈控制和扰动补偿。利用TMS320F2812DSP在实际的PMSM上进行了试验测试。试验结果表明，提出的控制方案可在多种负载条件下实现快速、平稳、准确的位置伺服控制，且对模型参数摄动也具有一定的鲁棒性。该控制方案可推广应用于相关领域的伺服控制系统。

【参考文献】

[1] 邹金红，朱玉川.基于复合前馈控制的交流位置伺服系统动态特性[J].电机控制与应用,2011,38(1)： 29-32.

[2] 余智胜，赵燕伟.皮革数控裁剪机伺服进给系统的设计与仿真[J].机电工程,2013,30(4)： 464- 467.

[3] ANG K H, CHONG G, LI Y. PID control system analysis, design, and technology[J]. IEEE Transac-tions on Control Systems Technology, 2005, 13(4)： 559-576.

[4] HEERTJES M, SCHUURBIERS X, NIJMEIJER H. Performance-improved design of N-PID controlled motion systems with applications to wafer stages[J]. IEEE Transactions on Industrial Electronics, 2009, 56 (5)： 1347-1355.

[5] SHIN H B, PARK J G. Anti-windup PID controller with integral state predictor for variable-speed motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3)： 1509-1516.

[6] 史伟民，路丰瑜，沈加海.基于输入和误差补偿的PMSM迭代学习控制[J].机电工程,2012,29(12)： 1461-1463.

[7] 陈昊,周建亮,王永,等.永磁同步电机速度跟踪控制[J].电力电子 技术,2013,47(6)： 100-102.

[8] PENG K M, CHENG G Y, CHEN B M, et al. Imp-rovement of transient performance in tracking control for discrete-time systems with input saturation and disturbances[J]．IET-Control Theory & Applications, 2007, 1(1)： 65-74.