带二元约束非凸三次优化问题的全局充分条件*

张 亮

(重庆师范大学 数学学院，重庆 401331)

考虑下面的带有双值约束的非凸三次优化问题：

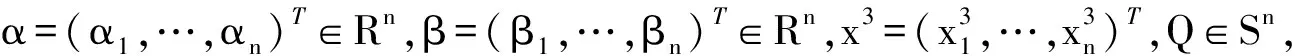
三次规划数学模型(CP)包含了一大类最优化问题，包括二次优化问题和组合优化问题等，它在三次多项式近似优化、凸优化、工程设计和结构优化等领域有着广泛的应用.此外，由于二次优化问题是三次规优化问题的特殊情形，所以关于三次问题的研究成果可以应用到二次规划问题，见文献[1-12].此处主要考虑一类带有双值约束的非凸三次优化问题(CP)，利用该非凸三次优化问题的特殊性将问题(CP)等价转化为带有双值约束的非凸二次规划问题进行研究，并利用Rockafellar在文献[11]中给出的经典对偶理论，提出了等价转化后的非凸二次规划问题的一些全局充分条件，并利用问题的等价性得到了相应的非凸三次优化问题全局充分条件.

1 预备知识

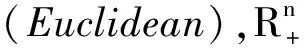
定义1 设x*∈{-1，1}n，如果f(x*)≤f(x)对任意的x∈{-1，1}n都成立，则称x*是问题(CP)的一个全局极小点.

对于问题(CP)，因为x∈{-1，1}n，所以x3=x，因此能够容易证明问题(CP)等价于式(1)的带有双值约束的非凸二次优化问题：

(1)

由于(CP)等价于问题(BQP)，所以通过研究问题(BQP)的全局最优性条件来得到问题(CP)的全局最优性条件.问题(CP)的可行集{-1，1}n可以等价地写成式(2)的连续形式：

(2)

下面的引理是很显然的.

引理1 设x*∈{-1，1}n，则x*是问题(CP)的全局最优解当且仅当x*是问题(BQP)的全局最优解.

对于一个n×n实对称矩阵Q=(qij)，qij=qji，i，j=1，2，…，n，用λi(Q)≡λi表示Q的特征值，且约定

λ1≥λ2≥…≥λn

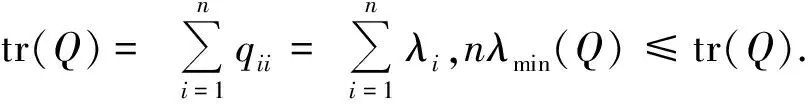
2 主要结果

考虑下面的非凸二次规划问题(QP)：

这一节，通过问题(QP)推导出问题(CP)全局最优性充分条件.

设u=(u1，…，un)T∈Rn是相应于问题(QP)的约束集(2)的拉格朗日乘子向量，则问题(QP)的拉格朗日函数可以表示为

(3)

令U=diag(u)，则式(3)可以变形为

(4)

则可以定义相应的问题(QP)的对偶问题为式(5)的凹最大化问题：

(DQP) sup{h(u)：u∈Rn∩domh}

(5)

其中h是对偶函数，且有

h(u)：=inf{L(x，u)：x∈Rn}

(6)

以及domh={u∈Rn：h(u)>-∞}.由标准的对偶性可知，下面的弱对偶关系总是成立的：

f(x)≥h(u)，∀x∈S，∀u∈Rn∩domh

因为问题(QP)是非凸的，所以强对偶关系在这里不成立.下面，先回顾文献[11]中所提出的基本对偶理论.

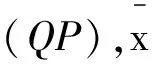
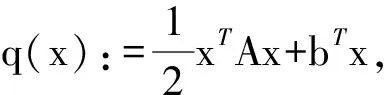
(i) 存在向量x∈Rn，使得Ax+b=0；(ii) A是半正定矩阵，即A±0.

应用引理2，3，可以得到判断问题(CP)的一个可行点为全局最优解的充分条件.

定理1 (问题(CP)的全局充分性条件) 设Q是实对称矩阵，α，β∈Rn，λn(Q)为Q的最小特征值，设x是问题(QP)的一个可行解，并且X=diag(x)，如果

[SC]XQXe+X(α+β)≤λn(Q)e

那么x是问题(QP)的全局极小点，进一步，x也是问题(CP)的全局极小点.

证明对由式(4)和(6)所定义的对偶函数h应用引理3，有inf{L(x，u)：x∈Rn}>-∞当且仅当下面的两个条件(7)(8)成立：

∃x∈Rn：(Q+U)x+α+β=0

(7)

Q+U±0

(8)

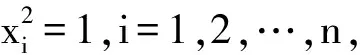
u：=-(XQXe+X(α+β))

(9)

首先，证明(x，u)满足式(7).事实上，由x=Xe，Ux=Xu，X2=I以及式(9)定义的向量u，有

(Q+U)x+α+β=QXe+UXe+α+β=QXe+Xu+α+β=

QXe-X2(α+β)-X2QXe+α+β=0

所以，式(7)成立.从而用式(7)可以将对偶目标函数h重新写成

其中x满足式(7).

其次，证明式(8)也成立.事实上，由已知条件和式(7)有

λn(Q)≥max1≤i≤n(XQXe+X(α+β))i=-λn(U)

所以，λn(Q+U)≥λn(Q)+λn(U)≥0，故Q+U±0，即式(8)成立.从而由引理3知，h(u)=inf{L(x，u)：x∈Rn}>-∞.这意味着u对于对偶问题(DQP)是可行的.由式(7)，对x=Xe，u=-XQXe-Xα-Xβ，有

再由引理2可知，x是问题(QP)的全局极小点.进一步，因为问题(QP)和问题(CP)是等价的，所以x也是问题(CP)的全局极小点.

注1 定理1只是充分条件，而不是必要条件，反例如下：

例1 考虑下面的优化问题：

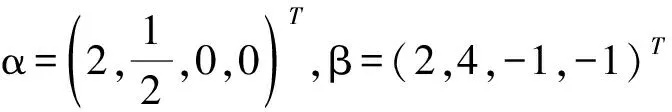
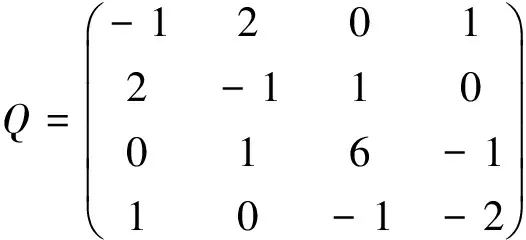
由前面的讨论可知，(EP1)可以等价地转化为二次规划问题QP1来处理：

考虑点x*=(-1，-1，1，1)T，注意到这里的问题(QP1)恰为文献[4]中的例2.1，而由文献[4]中的例2.1知，x*=(-1，-1，1，1)T是(QP1)的全局极小点，从而它也是问题(EP1)的全局极小点.通过简单的计算容易得到

从而X*QX*e+X*(α+β)≤λmin(Q)e不成立，即定理1中的条件[SC]不成立.所以定理1中的条件只是充分条件并不是必要条件.

参考文献：

[1] BECK A，TEBOULLE M. Global Optimality Conditions for Quadratic Optimization Problems with Binary Constraints[J]. SIAM J OPTIM，2000，11(1)：179-188

[2] RUBINOV A M，WU Z Y. Optimality Conditions in Global Optimization and Their Applications[J].Math program，2009，120(2)：101-123

[3] WU Z Y，RUBINOV A M. Global Optimality Conditions for Some Classes of Optimization Problems[J].J Optim Theory Appl，2010，145(3)：164-185

[4] JEYAKUMAR V，RUBINOV A M，WU Z Y. Sufficient Global Optimality Conditions for Non-convex Quadratic Minimization Problems with Box Constraints[J].J Glob Optim，2006，36(3)：471-481

[5] JEYAKUMAR V，RUBINOV A M，WU Z Y. Non-convex Quadratic Minimization Problems with Quadratic Constraints：Global Optimality：conditions[J]. Math.Program(A)，2007，110(3)：521-541

[6] ZHANG X M，WANG Y J，MA W M. Global Sufficient Optimality Conditions for a Special Cubic Minimization Problem[J]. Mathematical Problems in Engineering，2012，3(7)：178-192

[7] WU Z Y，BAI F S. Global Optimality Conditions for Mixed Nonconvex Quadratic Programs[J]. Optimization，2009，58(1)：39-47

[8] HIRIART-URRUTY J B. Global Optimality Conditions in Maximizing a Convex Quadratic Function under Convex Quadratic Constraints[J]. Journal of Global Optimization，2001，21(4)：445-455

[9] HIRIART-URRUTY J B. Conditions for Global Optimality 2[J]. Journal of Global Optimiza-tion，1998，13(4)：349-367

[10] STREKALOVSKY A. Global Optimality Conditions for Nonconvex Optimization[J]. Journal of Global Optimization，1998，12(4)：415-434

[11] ROCKAFELLAR R T. Convex Analysis[M]. Princeton：Princeton University Press，1997

[12] CHEN W，ZHANG L S. Global Optimality Conditions for Quadratic 0-1 Optimization Problems[J].J Glob Optim，2010，46(3)：191-206