考虑地铁换乘客流的 BRT 运营调度模型研究

吴家庆,宋 瑞,林 正,李树彬

(1. 北京交通大学 交通运输学院,北京 100044;2. 北京公共交通控股(集团)有限公司,北京 100161; 3. 山东省计算中心,济南 250014)

考虑地铁换乘客流的 BRT 运营调度模型研究

吴家庆1,2,宋 瑞*1,林 正2,李树彬3

(1. 北京交通大学 交通运输学院,北京 100044;2. 北京公共交通控股(集团)有限公司,北京 100161; 3. 山东省计算中心,济南 250014)

针对高峰期间地铁换乘的大客流对快速公交运营调度的影响,本文以快速公交运送乘客量最大化、乘客成本最小化、运营成本最小化为目标,建立了多目标规划模型,并设计了启发式求解算法.通过案例研究,可以得出最优发车间隔为 2 min,但存在客流损失,如果保证客流不损失则发车间隔只能是 1 min,但运营成本大幅增加,而且存在严重的运力浪费;在容忍度从 5 min 到 15 min 的变化过程中,各项指标值( 包括最优解)都没有变化,仅仅乘客等车成本和总成本呈阶梯变化,即在大客流情况下最优发车间隔对容忍度不敏感.在 BRT 实际运营调度中,应综合权衡各方利益,根据实际需求考虑发车间隔大小.

交通工程;快速公交;发车间隔;运营调度;启发式算法

1 引 言

快速公交(BRT)是利用改良型的公交车辆,运营在城市公共交通专用道路空间上,保持轨道交通特征并且仍然具备常规公交的便利和快速的公共交通方式.由于投资相对低廉、运营效果显著,目前已经成为世界各大城市解决交通拥堵的首选项目.自2005 年北京南中轴 BRT1 线开通运营以来,BRT便迅速在我国推广.短短数年间,中国已经成为全球范围内 BRT 应用最广泛的国家.

一般而言,BRT 运营在城市大客流走廊上,线路走向基本上是从市中心向郊区发散,在市中心区与地铁等大运量交通方式衔接,以北京为例,四条BRT 线的首站在市中心区都与地铁2 号线衔接.因此,作为地面公交系统的一部分,BRT 系统与轨道交通的衔接是一个重要的课题.如何沿轨道交通线优化接运公交网络(feeder bus network design problem,FBNDP),相关学者做了大量工作.国外的Vuchic[1],Chien 和 Schonfeld[2],Kuan[3]提出了线网布设的寻优算法和优化方法;国内的蒋冰蕾和孙爱充[4]、 许旺土[5]等也完成了此方面的研究. 在BRT运营调度方面,Ceder[6],Zolfaghari S[7], Shrivastava P[8]等专家学者对城市快速公交确定发车频率和发车时刻表的数学规划方法进行深入的理论研究并取得了丰硕的成果;国内对公交发车间隔和时刻表的研究也比较深入,代表性的有宋瑞[9]、孙杨[10]、刘志刚[11]等.相关文献基本上都是对确定性约束条件下的公交发车间隔问题进行的研究,很少涉及浪涌式大客流对运营调度的影响,尤其是线路首站大客流常态化的情况.

本文针对 BRT首站和地铁接驳换乘大客流常态化的情况,对已有的运营调度研究成果进行适当改进,以 BRT 运送乘客量最大化、乘客成本最小化、运营成本最小化为目标,建立综合数学模型,并应用启发式算法求解.对于给出的案例,获得最优发车间隔,对发车间隔和乘客容忍度进行灵敏度分析,验证模型和算法的有效性,使得到的发车间隔大小匹配实际客流需求.

2 问题描述及假设

BRT 首站与轨道交通站点接驳后,高峰期间地铁每个间隔内换乘 BRT 的客流往往超过了 BRT车辆的容量.因此,BRT 必须采取比地铁更小的发车间隔才能满足换乘客流的要求,但是运营成本会大幅提高.如果 BRT 发车间隔过大,首站排队人数会大幅增加,当排队时间过长时,乘客可能会乘坐其他交通方式.综上,大客流情况下 BRT 发车间隔优化目标包括 3 个:①最大化接运公交乘客数(最小化损失乘客数);②最小化乘客成本;③最小化运营成本.

本文主要研究 BRT 首站与地铁接驳的情形,实际情况可能存在 BRT 线路与多个地铁站点接驳的情况,可将本文的方法相应地进行扩展.因此,假设条件如下:

(1)BRT 首站与轨道车站在同一地点,研究时段( 高峰期间) 地铁发车间隔不变(2 min),BRT 在研究时段内均匀发车,该发车间隔是需要优化的变量.

(2)BRT 车辆在车站间的运行速度为匀速,即车站间的运行时间是确定的.

(3)只考虑 BRT 首站到其他站点的客流 OD,不考虑其他站之间的 OD,而且首站到其他站点的客流均匀分布,主要目的是研究首站大客流对BRT发车间隔的影响.

(4) 只考虑站站停模式,不考虑其他调度形式.

(5)BRT 车辆采用统一容量的车型.

(6)乘客按照到达先后时间排队上车,不存在后到先上的问题,并且 BRT 车辆到站后等待的乘客立刻全部登上车辆.

(7)乘客到达 BRT 站点时,如果队长大于车辆容量,则换乘其他交通方式,否则加入队列继续等待;乘客能知道 BRT 下一次车到达的时间,如果等车时间超过容忍时间也乘坐其他交通方式.

(8)当 BRT 发车间隔不能被模拟时长整除时,在最后时刻发一次车,目的是运走最后排队的乘客.

3 模型建立

3.1 参数定义

T——研究时长(min);

hs——地铁发车间隔(min);

hB——BRT 发车间隔(min);

hmin,hmax——BRT线路最小、最大发车间隔(min);

tr——乘客候车容忍时间(min);

CA——BRT 车辆容量;

L——BRT 线路长度;

S——BRT 线路站点数;

Ls——BRT 首站到第 s 站点的距离(km),s= 1,2,…,S;

V——BRT 运送速度(km/h);

LD——BRT 线路最大断面满载率(%);

I——研究时段内地铁到达车次;

J——研究时段内 BRT 发车车次;

Δtij——地铁第 i 次车到达时间与 BRT 第 j次车发车时间的差(min),———研究时段内地铁第 i次车下车的乘客数,i=1,2,…,I;——地铁第 i次车离开的乘客数,i=1,2,…,I;——地铁第 i次车排队等候的乘客数,i= 1,2,…,I,

QS——研究时段内地铁换乘 BRT 的乘客总数,

qB———研究时段内 BRT 第 j次车运送的乘客

QB——研究时段内 BRT 运送的乘客总数,

QL——研究时段内乘客的损失数,

F1——乘客成本(元);

F11——乘客等车成本(元);

F12——乘客乘车成本(元);

F2——运营成本(元);

C1——公交乘客量的费用转换系数(元/人);

C2——乘客的时间费用转换系数(元 /min);

C3——运营距离费用转换系数(元/km).

3.2 模型分析

按照上节描述,优化目标要在运送的乘客数、乘客成本与运营成本之间进行权衡.

(1)运送的乘客数.

(2)乘客成本.

假设所有乘客的时间价值相同,乘客成本正比于总出行时间(包括等车时间与乘车时间),表示为

(3)运营成本.

假设运营成本正比于车辆运行的距离,运营成本表示为

3.3 模型整合

按照上节描述,模型需要综合决策发车间隔与运送乘客总量.从系统的观点出发,优化目标要在运送的乘客数、乘客成本与运营成本之间进行权衡.因此可表示为多目标规划模型:

maxQB=maxf,minF1,minF2

采用线性加权法将多目标规划问题变为单目标规划问题:

目标(4)表示最小化加权后的总目标,ε、κ、λ为多目标权重系数,表示各个目标的相关重要程度,ε+κ+λ=1.对于 ε、κ、λ 的取值,可以选用特尔菲法,请公交专家、公交规划部门的决策者在互不干扰的情况下对权重系数发表意见,然后计算权重系数的期望值.约束(5)表示发车间隔限制,其中hmin、hmax分别表示线路最小、最大发车间隔.

3.4 模型求解

上述模型可用启发式算法求解,算法整体流程如图1所示,具体描述如下:

图1 算法流程图Fig.1 Algorithm flowchart

Step1根据 hmin、 hmax, 采用枚举法列举所有可能 H_element的集合 H_set;

Step2选择 H_set 中的一个 H_element,计算运营成本;

Step3BRT 第 1 次发车,根据 hs与 hB的关系,判断 BRT 本间隔内包含的地铁车次,再根据Δtij与计算排队客流和损失客流;

Step4根据的关系,判断 BRT 本间隔内包含的地铁车次是否已计算完毕,如果没有计算完毕,转入下一个地铁车次.否则计算 BRT 本车次运送的乘客数和乘客成本,并进入 BRT 第 2 次发车;

Step5当所有BRT车次计算完毕后,根据式(4)计算 F,并更新最优解 F*,然后转 Step2;

Step6判断 H_set 中是否所有的 H_element被检验完毕.如果没有,转 Step2;如果完毕,则输出最后结果.

4 案例研究

4.1 案例说明

BRT 线路长L为10km,6个车站(即 S 为 6),站间距为 2 km、1 km、2 km、3 km、2 km;运营时间 T为 6:00-7:00;地铁到达间隔 hS为 2 min;乘客容忍度 tr介于 5-15 min;BRT 运送速度 V 取 20 km/h; BRT 车辆容量 CA 取 150 人/辆;BRT 发车间隔hmin、hmax分别 取 1 min 和 15 min;多目标规划权重ε、κ、λ 分别取 0.2、0.4、0.4;费用转换系数 C1、C2、C3分别取4元/人、0.2 元 /min、2元/km;表1 是地铁每个间隔内到达的乘客数.

4.2 结果及分析

表2 是乘客容忍度 tr=5 min 时的运算结果.

表2 乘客容忍度 tr=5 min 时的计算结果Table2 Calculating results of passenger tolerance equal to 5 min

(1)在 6:00-7:00 时段内,在地铁每个间隔内换乘的乘客数几乎都超过 BRT 车辆容量的条件下(见表1),得到的最优发车间隔为 2 min,损失乘客数 532(占比 10.8%),如果要保证没有客流损失,只能采用极限发车间隔 1 min,但是各项成本指标都将增加,而且最大断面满载率仅为 54.5%,存在严重的运力浪费.在实际运营调度过程中,一般采取极限发车间隔来处理高峰大客流,但从理论上综合权衡而言,这样只是减少了客流损失,成本投入会极大增加.

表1 6:00-7:00 地铁每个间隔内到达的乘客数(人)Table1 Passenger number at every interval of subway during 6:00-7:00(persons)

(2) 从图3-图5 可看出,随着发车间隔的增大,运送乘客数降低,而损失乘客数增加;发车间隔增大,等车成本先增加后降低,而乘车成本及乘客总成本不断降低,当然,运营成本也不断降低;对于最大断面满载率而言,除了发车间隔为 1 min 时较低外,其值介于 96.7%-98.9%.

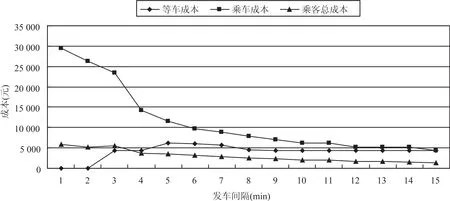
图4 发车间隔与等车成本、乘车成本及乘客总成本的关系曲线Fig.4 Relationship between headway and waiting cost and carrying cost and total cost

图5 发车间隔与最大断面满载率的关系曲线Fig.5 Relationship between headway and maximum section load rate

对乘客容忍度 tr从 5-15 min 的研究结果表明(鉴于篇幅,本文不一一列表),在地铁每个间隔内换乘的乘客数几乎都超过 BRT 车辆容量的条件下,得到的最优发车间隔都是 2 min,而且在最优目标解的情况下,其他各项指标都保持不变.但是,不同的发车间隔,乘客等车成本和总成本是不断变化的,如表3所示.

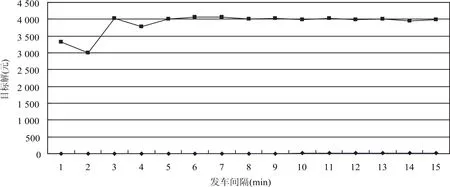
图2 发车间隔与目标值的关系曲线Fig.2 Relationship between headway and target value

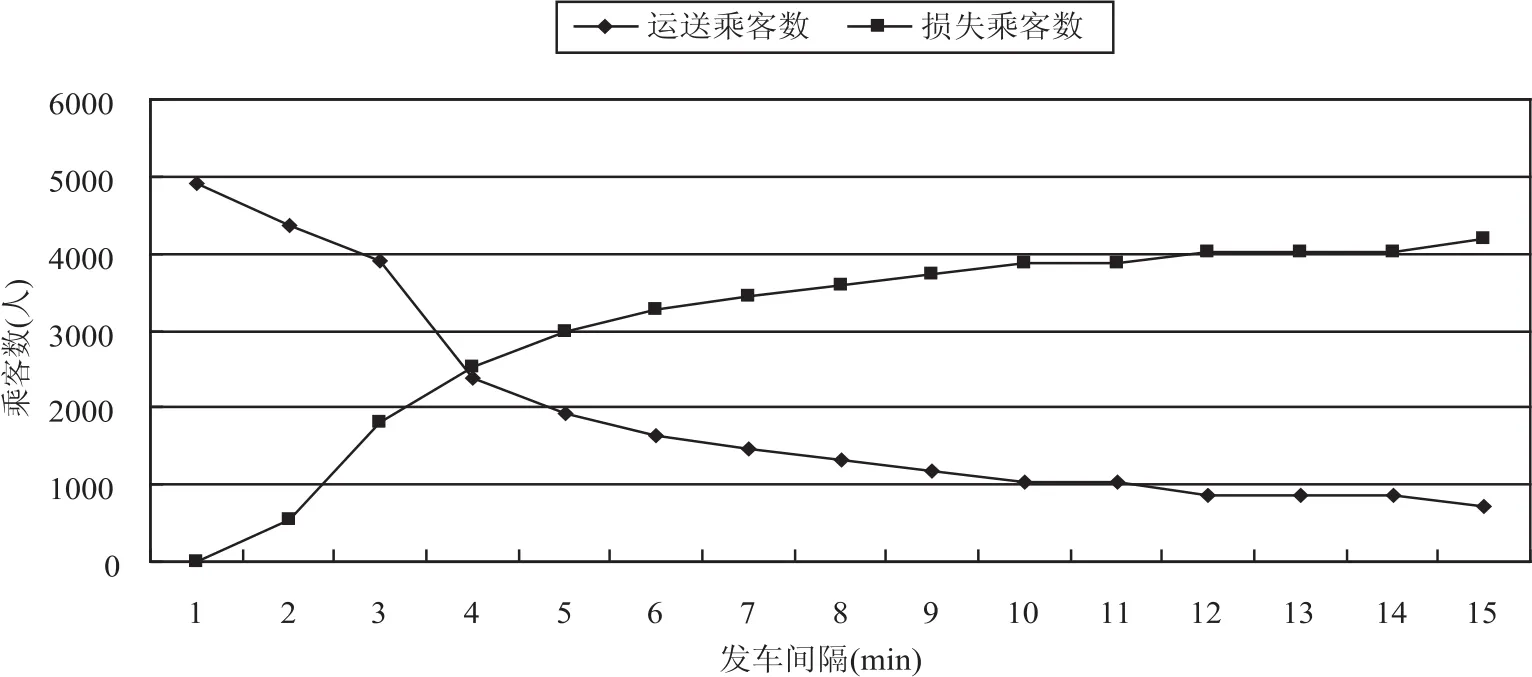
图3 发车间隔与运送乘客数及损失乘客数的关系曲线Fig.3 Relationship between headway and carrying and loss passenger number

表3 容忍度(5-15 min) 与乘客等车成本关系表( 元)Table3 Relationship between passenger tolerance(5-15 min)and waiting cost(yuan)

图6 容忍度与乘客等车成本关系曲线Fig.6 Relationship between passenger tolerance and waiting cost

从表3和图6可以看出,随着发车间隔和容忍度的变化,乘客等车成本是阶梯变化的.产生这样现象的主要原因首先是每个间隔内到达的客流几乎都超过了 BRT 车辆容量,在 BRT 两个车次之间尽管运送的乘客数 150 人不变,但是这 150 人是先到先排队,所以随着容忍度的增加而阶梯变化.其次,本文的最优间隔 2 min 小于容忍度 5-15 min,即最优间隔对容忍度不敏感,其结果必然是其他各项指标都没有变化,仅仅乘客等车成本和总成本变化,当采用低峰客流数据时,其他指标值(包括最优解)将对容忍度非常敏感.

5 研究结论

本文针对高峰期间地铁换乘大客流对 BRT 运营调度的影响,以 BRT 运送乘客量最大化、乘客成本最小化、运营成本最小化为目标,建立了多目标规划模型,并设计相应的启发式算法.通过案例的研究,可以得出最优发车间隔为 2 min,但存在客流损失(占比 10.8%),如果要保证客流没有损失发车间隔只能是 1 min,但是运营成本将大幅增加,而且最大断面满载率仅为 54.5%,存在严重的运力浪费,因此在实际运营调度中,应综合权衡各方利益,可以允许部分客流损失.在大客流情况下,最优发车间隔对容忍度不敏感,在容忍度从 5 min 到 15 min 的变化过程中,各项指标值(包括最优解)都没有变化,仅仅乘客等车成本和总成本呈阶梯变化.可预测当采用低峰客流数据时,各项指标值(包括最优解)将对容忍度非常敏感.

[1] Vuchic V R.Urban transit:operation,planning,and economics[M].Hoboken,New Jersey:John Wiley& Sons,Inc.,2004.

[2] Chien S,Schonfeld P.Joint optimization of a rail transit line and its feeder bus system[J].Journal of Advanced Transportation,1998,32(3):253-284.

[3] Kuan S N,Ong H L,Ng K M.Solving feeder bus network design problem by genetic algorithms and ant colony optimization[J]. Advances in Engineering Software,2006,37(6):351-359.

[4] 蒋冰蕾,孙爱充.城市快速轨道交通接运公交路线网规划[J].系统工程理论与实践,1998(3):130-134. [JIANG BL,SUN AC.Urban rapid rail transit feeder buses routes planning[J].System Engineering Theory &Practice,1998(3):130-134.]

[5] 许旺土,何世伟,宋瑞,等.基于改进遗传算法的接运公交线路生成优化模型[J].北京交通大学学报, 2009,33(3):40-44,51.[XU WT,HE SW,SONG R, et al.Route generation optimization model for feeder bus based on advanced genetic algorithm[J],Journal of Beijing Jiaotong University,2009,33(3):40-44,51.]

[6] Ceder A,Tal O.Timetable synchronization for bused Computer-aided scheduling of Public transport[M]. Springer,NewYork.1999:245-258.

[7] Zolfaghari S,Azizi N,Mohamad Y J.A model for holding strategy in public transit systems with real-time information[J].InternationalJournalofTransport Management 2004,2:99-110.

[8] Shrivastava P,Mohony M O.A model for development of optimized feeder routes and coordinated schedules a genetic algorithms approach[J].Transportation Policy. 2006,13:413-425.

[9] 宋瑞,何世伟,杨永凯.公交时刻表设计与车辆运用综合优化模型[J].中国公路学报,2006,19(3):70-76.[SONG R,HE SW,YANG YK.Integrated optimization model of transit scheduling plan and bus use[J].China Journal of Highway and Transport, 2006,19(3):70-76.]

[10] 孙杨,宋瑞,何世伟.弹性需求下的接运公交网络设计[J].吉林大学学报(工学版),2011,41(2):349-354.[SUN Y,SONG R,HE SW.Feeder bus network design under elastic demand[J].Journal of Jilin University(Engineering and Technology Edition), 2011,41(2):349-354.]

[11] 刘志刚,申金升,王海星,等.基于协同发车的区域公交时刻表生成模型[J].交通运输运输系统与信息,2007,7(2):109-113.[LIU ZG,SHEN JS, WANG HX,et al.Regional public transportation timetabling model with synchronization [J]. Transportation Systems Engineering and Information, 2007,7(2):109-113.]

Study on Optimal Model of the BRT Operation Scheduling Considering Passengers Transferring from Subway

WU Jia-qing1,2,SONG Rui1,LIN Zheng2,LI Shu-bin3
(1.School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China; 2.Beijing Public Transport Holdings(Group)Co.,Ltd.,Beijing 100161,China; 3.Shandong Computer Science Center,Jinan 250014,China)

Considering the passengers transferring from subway impact on the BRT operation scheduling during the peak hours,in this paper the multi-objective programming model is proposed,which target to maximized passengers flow,minimized user cost and operation cost.A heuristic algorithm is developed to solve the model.By example,the optimal headways can be acquired and the value is 2 minutes,but in this case there is some passenger loss.The headway value only is 1 minute if ensuring no passenger loss,but the operating costs will substantially increase and there is a serious waste of capacity.All the index value have not changed including the optimal solution only the passengers waiting cost and the total cost in stepped variation when passenger tolerance change from 5 min to 15 min,that is to say,the optimal headway is not sensitive to passenger tolerance in the case of numerous passenger flow.The results also show that the headway should be made based on the actual demand.

transportation engineering;bus rapid transit(BRT);headways;operation;heuristic approach

1009-6744(2014)01-0150-08

U491

A

2013-06-13

2013-08-05录用日期:2013-10-12

国家重点基础研究发展计划(2012CB725403);北京市交通行业科技项目(KY2011-9);国家“十一五”科技支撑计划(2006BAJ18B04-06).

吴家庆(1978-),男,湖北天门人,工程师,博士生.*通讯作者:rsong@bjtu.edu.cn