异型管扭曲环向周期裂纹应力强度因子

张芳瑶，陈 松，蔡永梅，王 伟，谢禹钧(辽宁石油化工大学机械工程学院，辽宁抚顺 113001)

异型管扭曲环向周期裂纹应力强度因子

张芳瑶，陈 松，蔡永梅，王 伟，谢禹钧
(辽宁石油化工大学机械工程学院，辽宁抚顺 113001)

断裂是工程结构中常见的失效形式之一，控制结构断裂的重要参量是应力强度因子。本文以异型管周期裂纹为例，提出了利用J2守恒积分求解II型裂纹的应力强度因子方法。

周期裂纹管；裂纹；应力强度因子；J2积分守恒；异型管

异型管在工程结构中得到了十分广泛的应用，其常见缺陷为裂纹和类裂纹。含有环向周期裂纹的异型管是一种典型的三维结构。通常，对于无限大二维及三维弹性体裂纹问题，给出应力强度因子的解析解相对容易。但当考虑到边界对裂纹的影响时，如单边裂纹板条、三维薄壁有限边界裂纹等问题，给出满足边界条件的解析解相当困难[1]。这类问题通常可以通过数值解的方法进行求解。

近年来，谢禹钧[2-3]提出了利用积分守恒的方法来求解裂纹应力强度因子，该方法最大的特点是计算简单并且能够求解出封闭解。本文对受扭转载荷的环向周期裂纹管裂纹尖端的应力强度因子进行研究，并给出了利用J2守恒积分来求解II型应力强度因子的方法。

1 周期裂纹构形

异型管如图1所示，即设置十字加强筋的薄壁圆管，并带有环向周期裂纹和承受扭矩T作用。十字加强筋的厚度为tj，异性管中径为2R，厚度为t。

以下各节将给出利用J2守恒积分求解该异型周期裂纹管Ⅱ型应力强度因子的详细过程。

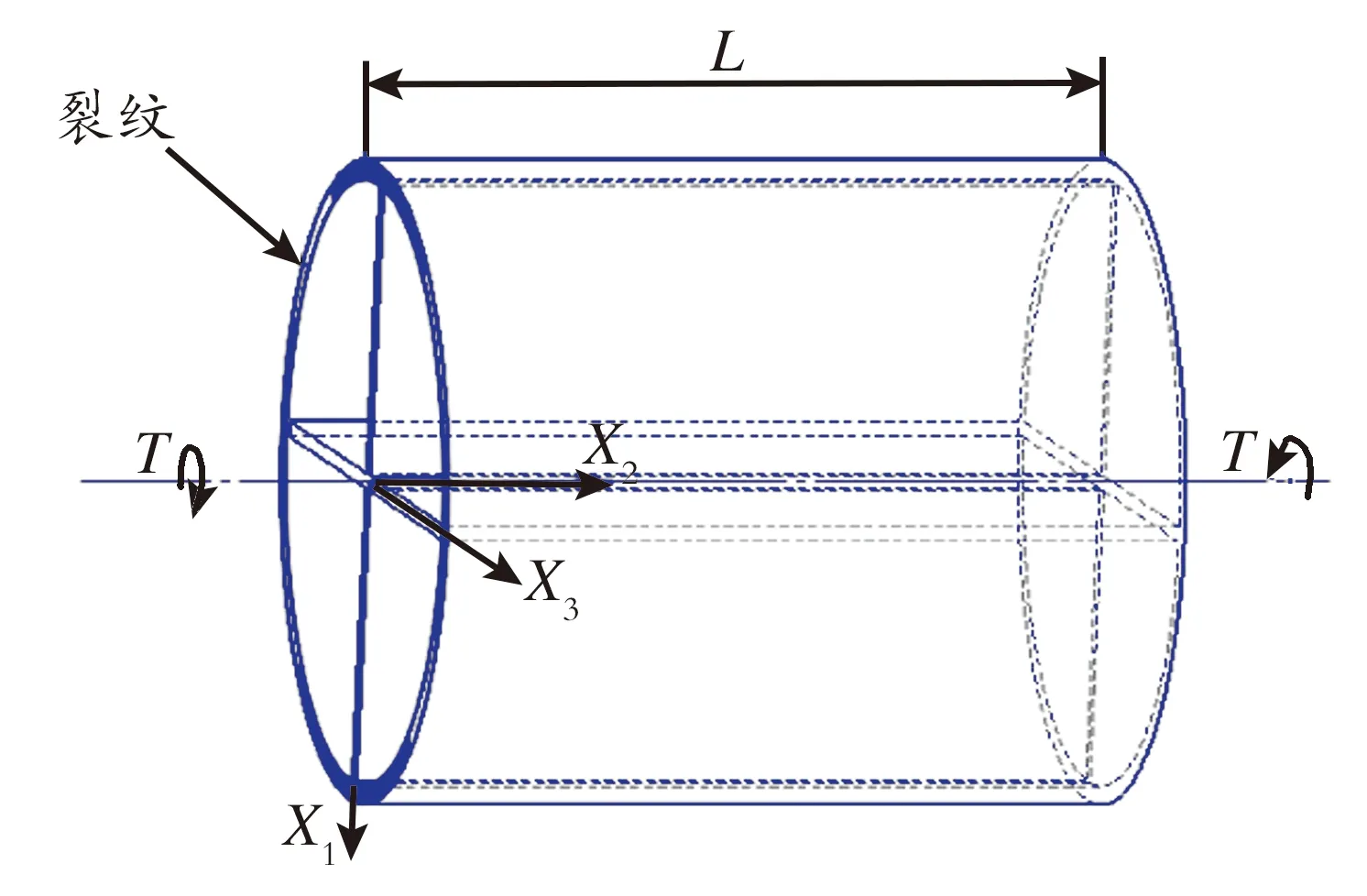
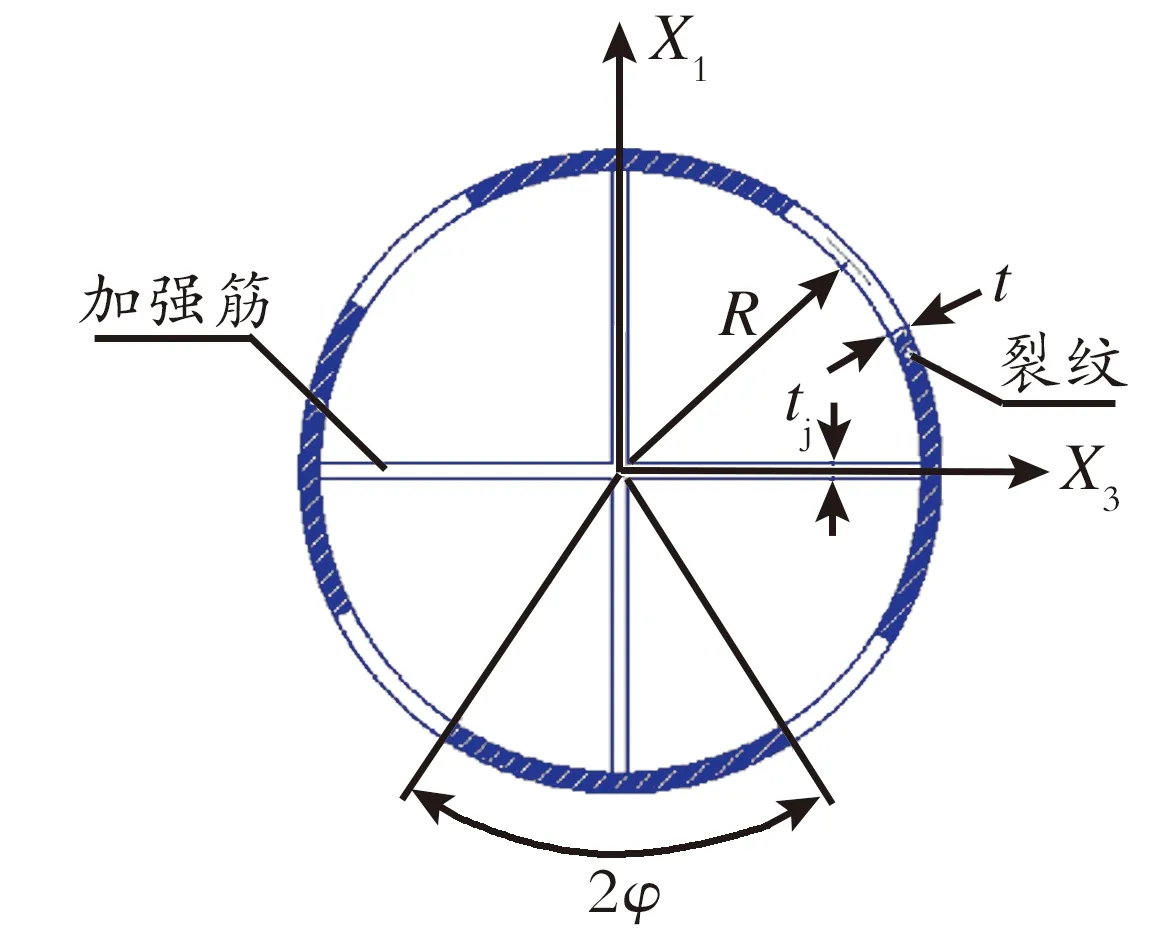
图1 受扭转载荷作用的周期裂纹管

Fig.1Special-shapedpipeswithperiodiccracks
subjectedtotorque

2 守恒积分

对于不含空穴的闭合曲面，以下积分为0[2-3]

积分式中的Ω为闭合曲面，w为应变能密度，Ti为面力，n为积分曲面的外法线矢量。本文将利用其中的J2守恒积分求解裂纹的应力强度因子。

对于二维静态边值问题，(1)式依然成立。对于Ⅱ型加载，取局部积分路径如图2所示。在裂纹尖端近场K控制区取积分路径saba′，其中sab为直线段，sba′为1/4圆弧线。用裂纹尖端近场的应力应变计算公式[4-5]可以计算出下列结果:

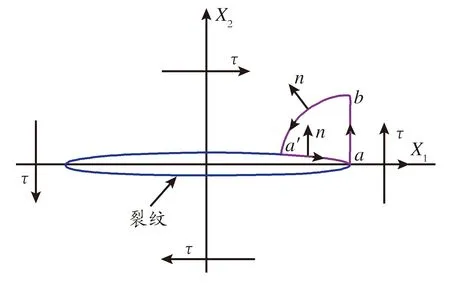
图2 裂纹尖端K控制区内的积分路径

Fig.2IntegralpathwithinK-dominantregion

对于图2中的闭合路径s=saba′-saa′，由积分守恒性[6-7]不难得出:

于是

3 异型周期裂纹管应力强度因子

异型管兼有三维壳体和细长梁构件的特征，于是可以将材料力学中的应力与变形计算方法应用于应力强度因子的计算。

3.1 闭合积分曲面

取闭合积分曲面如图3所示，由远场异型管横截面A+、异性管内外表面Bin(含筋板)和Bout、4个裂纹面Ωad、裂纹韧带横截面A-和裂纹尖端近场的8个1/4圆弧曲面组成。图3中裂纹的局部放大示意图如图4所示，其法线方向指向管壁的内侧。以上积分面上的J2守恒积分分别为:

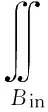
(7)

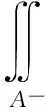
(9)

式中,θ为异型管单位轴线长度的扭转角，w为单位轴线长度的应变能密度。

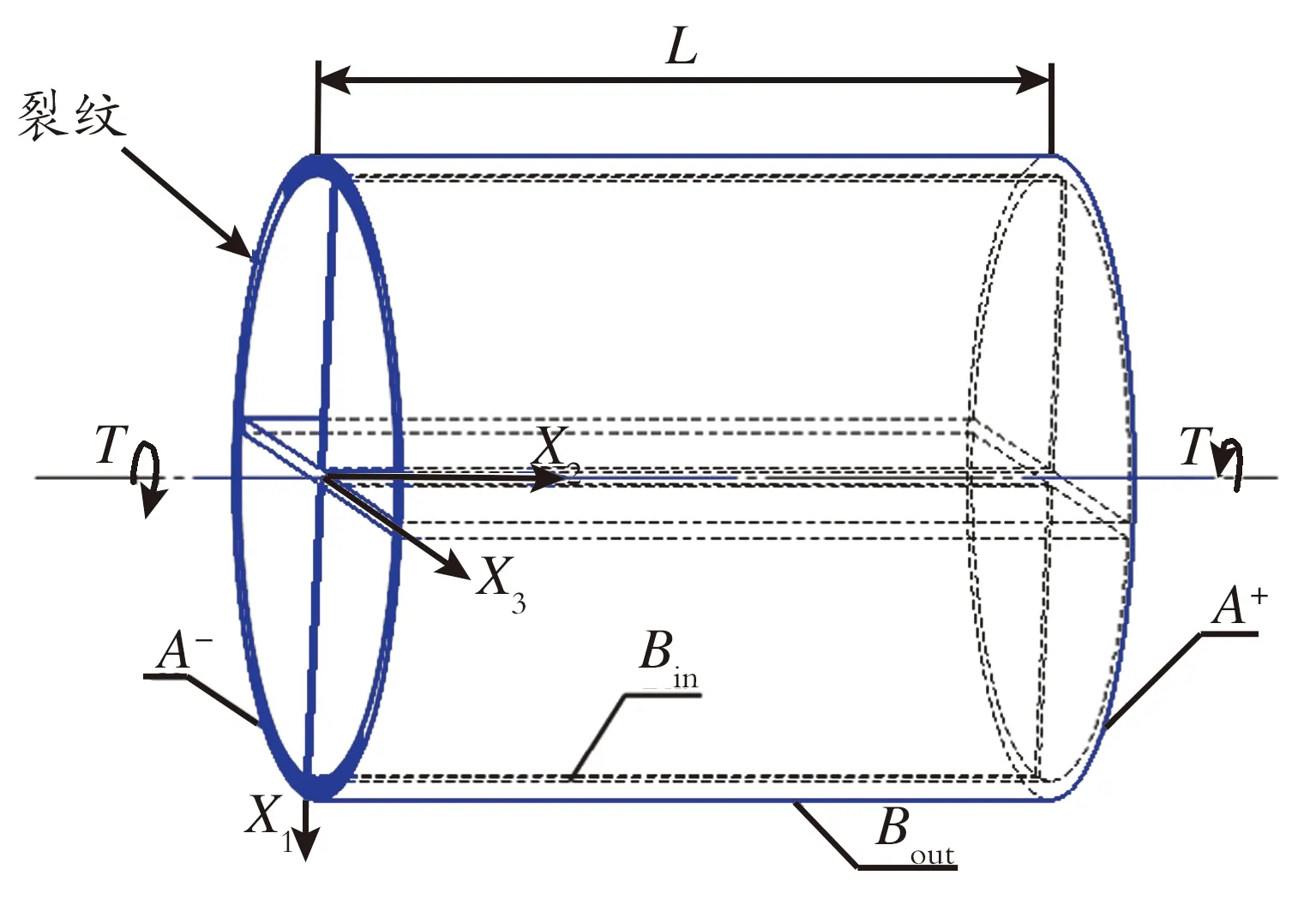
图3 异型管积分曲面

Fig.3Integralsurfaceforspecial-shapedtube

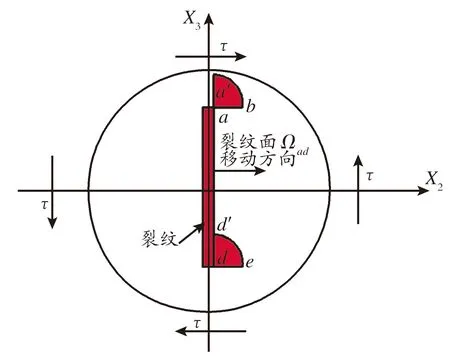
图4 裂纹周边局部管壁

Fig.4Localwallofthecrack

于是对于闭合曲面Ω=A++Bin+Bout+Ωad+A-，将(5)—(9)式代入(1)式可得:

在远场截面处单位轴线长度的扭转角为:

在裂纹韧带横截面上，利用椭圆裂纹模型，如图5所示，当椭圆孔的短半轴b→0时，此时的椭圆孔可近似为裂纹，于是裂纹韧带截面处的单位轴线长度扭转角可由下列极限求得:

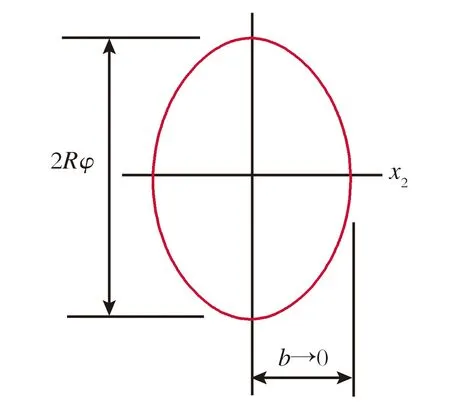
图5 裂纹管的椭圆模型(b→0)

Fig.5Ellipticalmodelforcracks(b→0)

3.2 应力强度因子

将(11)、(12)式代入(10)式，得:

(13)

正则化应力强度因子为:

4 数值算例与本文解比较

受扭转作用的环向周期裂纹管，其正则化应力强度因子由(14)式计算得出。数值计算采用ANSYS有限元分析软件，取材料的弹性模量E=200GPa，泊松比μ=0.3，单元类型为三维四节点shell181单元，裂纹尖端采用1/4节点奇异单元退化而成。异型截面管中径2R=400mm，异型管厚t=10mm，筋板厚度tj=10mm，管长L=1m。有限元网格图如图6所示。

图6 有限元网格(φ/φ0=0.44)

Fig.6Thefiniteelementmeshes(φ/φ0=0.44)

比较通过以上两种方法求解出的正则化应力强度因子，结果如图7所示。

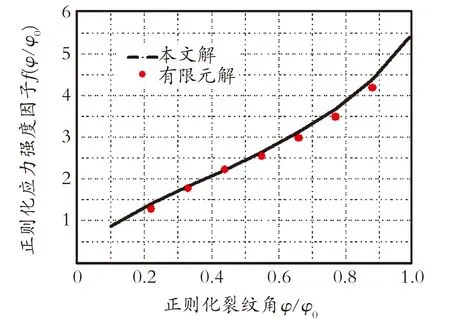
图7 本文解与有限元数值的比较(t/R=0.05,μ=0.3)

Fig.7Comparedwiththeresultsfromthefinite
elementanalysis(t/R=0.05,μ=0.3)

5 结论

利用J2守恒积分建立了一个求解受扭转载荷的环向周期裂纹管应力强度因子的一种方法。给出了扭转异型管环向周期裂纹边界的应力强度因子。数值分析结果表明该方法具有足够精度。用经典的方法求解含环向周期裂纹异型管的应力强度因子是存在困难的，但是应用本文给出的方法来求解却十分简单。

[1]王伟，蔡永梅，谢禹钧．椭圆形截面管环向裂纹应力强度因子分析方法[J]．工程力学，2011，28(11):197-201.Wang Wei, Cai Yongmei, Xie Yujun.An analytical method on stress intensity factor for circumferential cracked elliptical pipes[J].Engineering Mechanics, 2011，28(11):197-201.

[2]谢禹钧．弯曲载荷作用下工字形截面梁腹板中心穿透裂纹的应力强度因子[J]．机械强度，2006，28(3):397-400.Xie Yujun.Stress intensity factors for cracked I beams[J].Journal of Mechanical Strength, 2006，28(3):397-400.

[3]谢禹钧,王晓华，王伟，等.拉伸环向周期裂纹管的应力强度因子[J].工程力学, 2006，23(6):173-176.Xie Yujun,Wang Xiaohua,Wang Wei,et al.Stress intensity factors for circumferential periodic cracked pipes under tension[J].Engineering Mechanics, 2006，23(6):173-176.

[4]王晓华，段大文，谢禹钧.圆柱壳周期阵列压痕应力强度因子[J].石油化工高等学校学报，2011,24(5):80-82.Wang Xiaohua,Duan Dawen,Xie Yujun.Stress intensity factors for circumferential periodic flat indentation[J].Journal of Petrochemical Universities, 2011,24(5):80-82.

[5]徐芝纶.弹性力学[M].北京:高等教育出版社, 2008.

[6]Eshelby J D.The Force on an elastic singularity[J].Phil.Trans.Roy.Soc.London Ser.A, 1951, 244:87-112.

[7]Alabi J L,Sanders J L.Circumferential crack at the fixed end of a pipe [J].Engineering Fracture Mechanics, 1985,22(4):609-616.

[8]Xie Y J, Xu H, Li P N.Crack mouth widening energy-release rate and its application[J].Theoretical and Applied Fracture Mechanics, 1998,29(3):195-203.

[9]Xie Y J,Li P N, Xu H.On KⅠestimates of cracked pipes using an elliptical hole model and elementary beam strength theory of cracked beams[J].Engineering Fracture Mechanics, 1998, 59(3):399-402.

[10]Xie Y J.A theory on cracked pipe[J].International Journal of Pressure Vessels and Piping, 1998, 75:865-869.

(编辑 王亚新)

Stress Intensity Factor for Special-Shaped Pipes with Periodic Cracks

Zhang Fangyao, Chen Song, Cai Yongmei, Wang Wei, Xie Yujun
(SchoolofMechanicalEngineering,LiaoningShihuaUniversity,FushunLiaoning113001,China)

Fracture is an common type of failure for engineering structures，the stress intensity factor is an key parameter to control the cracked structures.In present work, a method to estimate the stress intensity factor by using the conservation law was proposed for the special-shaped pipes with periodic cracks under mode II loads such as torque.

Periodic crack pipe; Crack; Stress intensity factor;J2integral; Special-shaped pipes

1006-396X(2014)06-0093-04

2014-06-09

:2014-09-06

国家自然科学基金项目(50771052, 50971068, 11272141)。

张芳瑶(1988-)，女，硕士研究生，从事断裂力学和结构安全研究；E-mail:zhanglu8a@163.com。

谢禹钧(1960-)，男，博士，教授，从事断裂力学、结构完整性及失效风险等研究；E-mail:yjxie@lnpu.edu.cn。

TE905；O346.1

: A

10.3969/j.issn.1006-396X.2014.06.019