基于改进蚁群算法的梯式轨道多目标优化研究

金浩，刘维宁

1.绍兴文理学院土木工程学院，浙江绍兴 312000

2.北京交通大学土木建筑工程学院，北京 100044

基于改进蚁群算法的梯式轨道多目标优化研究

金浩1，刘维宁2

1.绍兴文理学院土木工程学院，浙江绍兴 312000

2.北京交通大学土木建筑工程学院，北京 100044

1 引言

随着城市轨道工程的大量建设，由轮轨耦合振动引起的环境振动问题日益受到关注。根据振动波的传播特性，地铁减隔振措施大致可分为：振源减振措施、传播途径隔振措施以及受振体隔振措施。梯式轨道凭借其良好的减振性能，近几年在我国得到大量应用。

对于梯式轨道减振性能的研究，国内外文献大致可归纳为：数值模拟[1-3]，譬如R J Hosking和F Milinazzo建立了周期点支撑作用下的无限长Bernoulli-Euler梁数学模型（模拟钢轨和纵向轨枕的耦合），分析了梯式轨道在稳态荷载作用下，随周期支撑质量和粘性阻尼变化的响应；现场测试[4-5]，譬如H Xia等对北京轨道交通5号线铺设有梯式轨道的高架试验段进行了测试，认为和普通无砟轨道相比，梯式轨道具有很好的减振特性；实验室分析[6-7]，譬如王文斌等采用锤击法，对梯式轨道进行了动力特性分析。但是，这些方法都只能对一个目标进行分析。在需要同时优化分析多个目标时，显得束手无策。

面对这个问题，本文尝试采用MO-FHACO（多目标觅食-返巢机制连续域蚁群算法），对梯式轨道进行双目标优化分析。

2 梯式轨道数学模型

梯式轨道选用60 kg/m钢轨，钢轨长lrail=6.15 m，单根钢轨质量mrail≈369 kg；扣件间距0.625 m，扣件刚度kur=60 MN/m，扣件垫板材料损耗因子ηur=0.2；纵向轨枕密度ρls=2 680 kg/m3，截面面积Sls=0.46 m× 0.185 m，长lls=6.15 m；枕下弹性垫板刚度kus，材料损耗因子ηus。梯式轨道如图1所示。

图1 梯式轨道

将梯式轨道简化为5个子系统（如图2所示）：钢轨子系统、扣件子系统、纵向轨枕子系统、枕下弹性垫板子系统以及道床子系统。

图2 梯式轨道简化图

钢轨子系统四端参数矩阵：

其中，S=SrailSurSlsSus，Frail为钢轨作用力，Vrail为钢轨作用速度，Ff为基础响应力，Vf为基础响应速度。

3 MO-FHACO算法原理

3.1 FHACO原理

1991年，Dorigo M[8]首次提出了蚂蚁系统（Ant System，AS），并成功地应用于旅行商问题。在接下来的20多年，AS算法得到极大发展，并从仅适用于组合优化问题拓展到连续域问题。

但是，这些衍生的蚁群算法都没有区分人工蚂蚁释放的“食物”信息素和“蚁巢”信息素，而是将两者统一为信息素。通过细致观察自然蚂蚁的觅食-返巢过程，提出“觅食-返巢”机制。人工蚂蚁从“蚁巢”出发，根据“食物”信息素到达“食物源”，同时释放“蚁巢”信息素；然后，根据“蚁巢”信息素返回“蚁巢”，同时释放“食物”信息素。[9]下面具体解释“觅食-返巢”机制：

设目标函数为f(x)，设计变量为x。其中，x∈[a,b]，a，b分别为设计变量x的最小值和最大值。通过数学换算，将目标函数f(x)转化为f(x′)，设计变量x转化为x′。其中，x=(b-a)x′+a，x′∈[0,1)。设置一个极小值ε，如果(1-x′)≤ε，则认为x′=1。根据问题的不同，设计变量x′可以取小数点后d位。

对于十进制数，除第1层和第(d+2)层只能取“0”外，中间d层每一层都可以取10个（0，1，…，9）数中的任意一个，如图3所示。

图3 “觅食-返巢”过程（十进制数字串）

设置n只蚂蚁从“蚁巢”出发。从“蚁巢”出发的蚂蚁j在k-1层的数字为Tfood(j,k-1)。其中，j=1,2,…,n，k=2,3,…,(d+2)。根据以下公式（1）选择下一层数字：

每只蚂蚁走完一层后，“蚁巢”信息素就需要局域更新：

当所有人工蚂蚁根据“食物”信息素找到“食物源”后，根据人工蚂蚁觅食过程留下的“蚁巢”信息素τnest返回“蚁巢”。在确定下一层的数字后，如何选取上一层的数字，判别方法与觅食过程相同。同样，“食物”信息素需要局域更新。

3.2 MO-FHACO算法实现

3.2.1构造初始Pareto最优解集

假如设计变量为x1和x2，其中，a1≤x1≤b1，a2≤x2≤b2。则，派遣两支蚂蚁军队，每支蚂蚁军队的蚂蚁数量为Num只。因此，第一支蚂蚁军队的每只蚂蚁驻守的值为：

同理，第二支蚂蚁军队的每只蚂蚁驻守的值为：

两支蚂蚁军队，设置信息交流机制。在每一只蚂蚁都有对应的设计变量值后，两支军队的蚂蚁互相交流，形成Num×Num对解。然后，从Num×Num对解中剔除非可行解，保留可行解。最后，比较可行解的目标函数值，得到初始Pareto最优解集。初始Pareto最优解集的设置，有利于提高MO-FHACO算法的散布性，避免传统蚁群算法收敛过快造成的Pareto最优前端稀疏的问题。

3.2.2 初始“食物”信息素更新

为避免蚂蚁在开始觅食时的盲目性，发挥初始Pareto最优解集对后续“觅食”蚂蚁的导引作用，具体实现为：

开始觅食时，蚂蚁应该循着“食物”信息素找到“食物源”。因此，对初始Pareto最优解对应的“食物”信息素进行加强。“食物”信息素加强公式为：

3.2.3 MO-FHACO算法流程

将MO-FHACO算法用商业软件Matlab编译[10]，流程如图4所示。

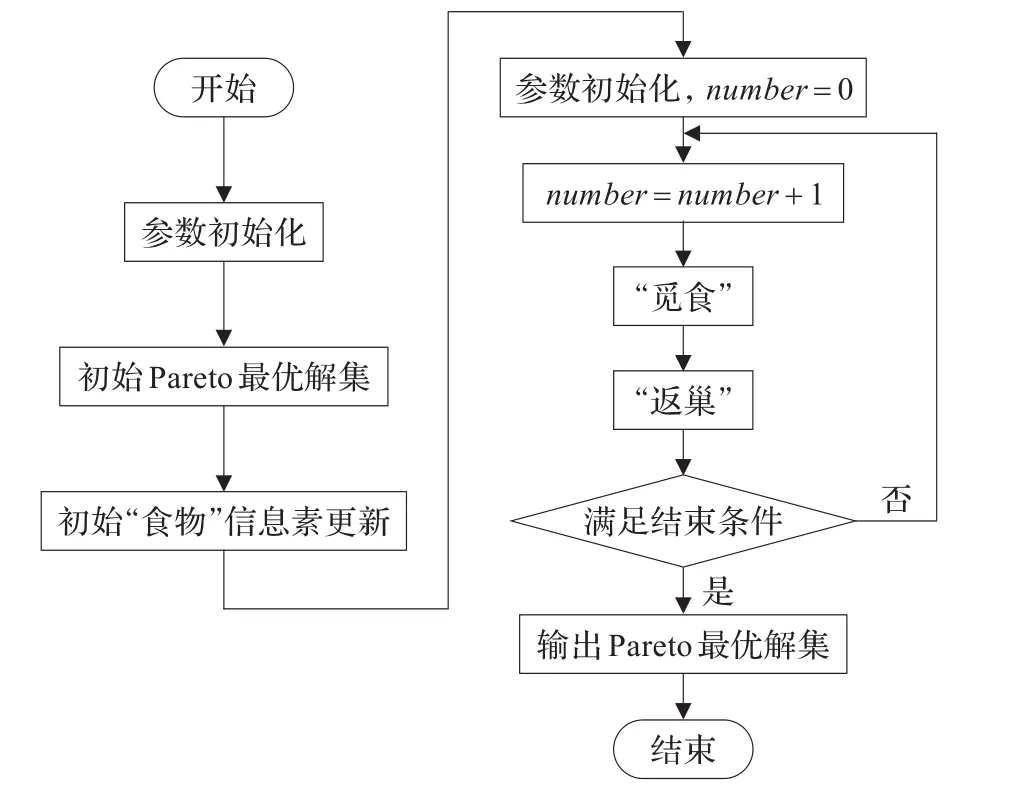
图4 MO-FHACO程序流程图

4 利用MO-FHACO对梯式轨道进行双目标优化

4.1 优化目标及设计变量

根据标准《UIC_513_1994_对于有关铁路车辆振动中评估乘客乘坐舒适性的指导》[11]的规定，乘客的舒适性以振动加速度作为评价指标；同时，根据标准《GB/T_ 13441.1_2007_机械振动与冲击人体暴露于全身振动的评价第1部分：一般要求》[12]的指导，如果已经确定低于1 Hz的频率范围对计权加速度值不重要，推荐使用1～80 Hz的频率范围。此处，假定钢轨振动和列车振动情况相一致，即标准UIC 513-1994中提到的车体（座位以及地板等）振动加速度可以用钢轨振动加速度来代替；并且，只考虑竖向振动加速度，不考虑其他两个方向的振动加速度。因此，将钢轨1～80 Hz振动加速度级作为优化目标1：

根据标准《GB_10070_1988_城市区域环境振动标准》[13]的规定，将Z振级作为环境振动评价指标。本文假定，地面测试结果可以用减振轨道支撑（整体道床）振动加速度来间接反映；进一步简化Z振级，用振动加速度级代替。同样，根据标准《GB/T_13441.1_2007_机械振动与冲击人体暴露于全身振动的评价第1部分：一般要求》[11]，如果已经确定低于1 Hz的频率范围对计权加速度值不重要，推荐使用1～80 Hz的频率范围。因此，将整体道床1～80 Hz的振动加速度级作为优化目标2：

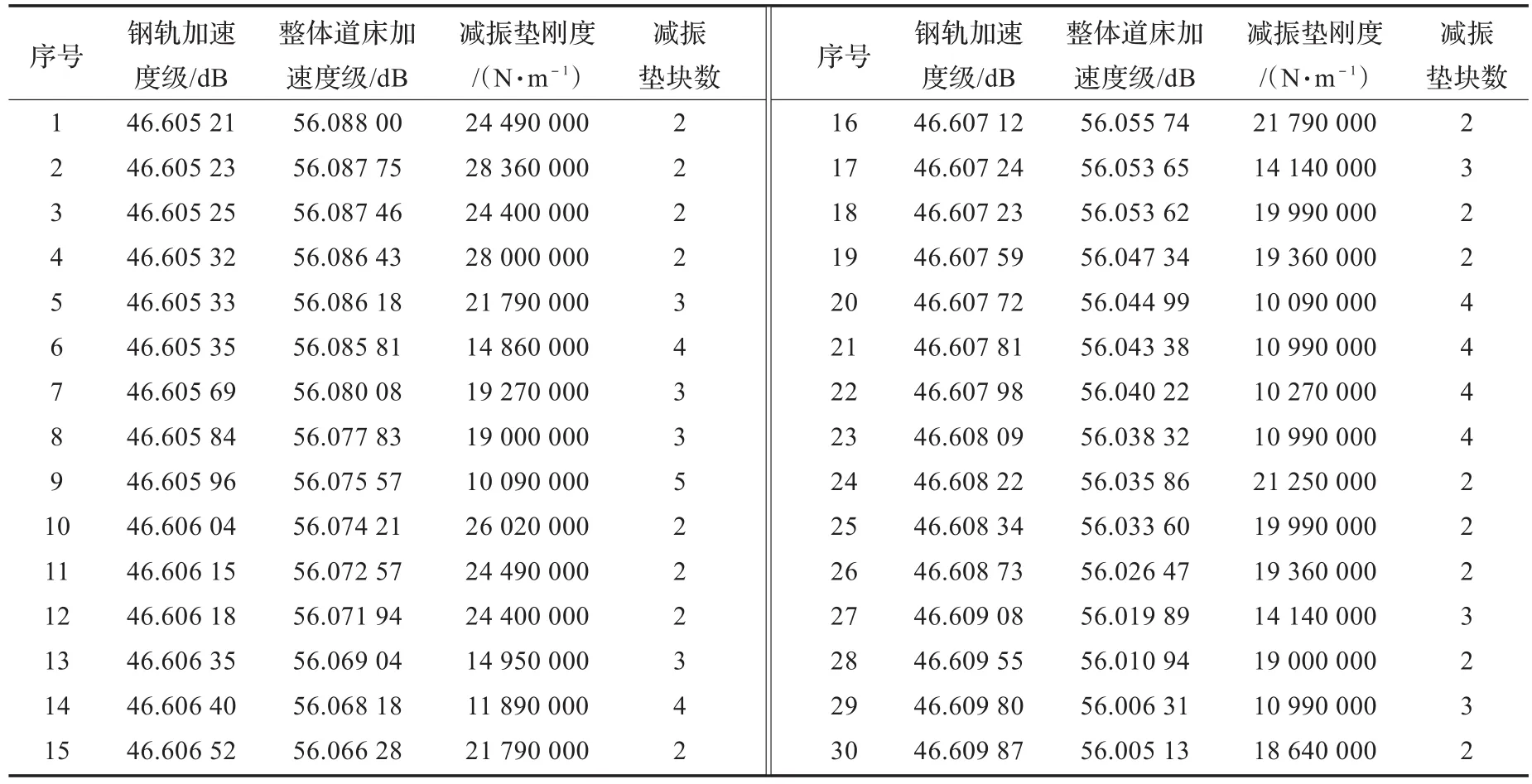
表1 优化目标及对应设计变量

通过单目标优化分析[14]，将枕下减振垫刚度kus作为设计变量1，枕下减振垫块数作为设计变量2。

枕下减振垫刚度kus取值范围为：

4.2 MO-FHACO参数设置

MO-FHACO参数设置如下：运行20次，小数位数d=3，判别常数Q0=0.3，“食物”信息素挥发系数ρfood=0.5，“蚁巢”信息素挥发系数ρnest=0.5，局域“蚁巢”信息素更新修正系数α=0.5，局域“食物”信息素更新修正系数β=0.5，蚂蚁数目n=10，迭代次数number=10。

4.3 优化应用

利用MO-FHACO耦合梯式轨道四端参数模型，得到MO-FHACO优化梯式轨道的结果，Pareto前端如图5所示。

具体应用如下：

假如在工程设计中，要求梯式轨道的整体道床振动加速度级在56～56.1 dB之间，钢轨振动加速度级在46.605～46.61 dB之前，图5所示。则对应设计变量（枕下减振垫刚度和枕下减振垫块数）共有30组，如表1所示。

对于优化目标，表1所示设计变量是无差别的，可根据其他工程因素，譬如枕下减振垫经济成本等，最终决定（对于设计变量枕下减振垫块数，采用四舍五入的方法，进行取值）。

图5 Pareto前端

5 结束语

本文以梯式轨道为例，利用MO-FHACO，对其乘客舒适性和梯式轨道减振性能进行了双目标优化分析。

耦合MO-FHACO和四端参数法数学模型，成功得到1～80 Hz频段钢轨振动加速度级和道床振动加速度级Pareto优化解，以及对应设计变量（枕下减振垫刚度和块数）。结果表明，采用MO-FHACO对梯式轨道进行多目标优化具有一定工程应用价值。

[1]Hosking R J，Milinazzo F.Modelling the floating ladder track response to a moving load by an Infinite Bernoulli-Euler beam on periodic flexible supports[J].East Asian Journal on Applied Mathematics，2012，2（4）：285-308.

[2]杨新文，和振兴.梯形轨枕轨道振动特性研究[J].振动工程学报，2012（4）：388-393.

[3]Liu X Z，Lian S L，Wei H L.Analysis on vibration reduction characteristics of ladder track structure on metro viaductundermeasuredtrackirregularities[J].Applied Mechanics and Materials，2012，226：406-410.

[4]邓玉姝，夏禾，善田康雄，等.城市轨道交通梯形轨枕轨道高架桥梁试验研究[J].工程力学，2011（3）.

[5]Xia H，Chen J G，Xia C Y，et al.An experimental study of train-induced structural and environmental vibrations of a rail transit elevated bridge with ladder tracks[J]. Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2010，224（3）：115-124.

[6]金浩，刘维宁，王文斌.梯式轨枕轨道模态试验分析[J].工程力学，2013（3）：459-463.

[7]王文斌，刘维宁，马蒙，等.梯形轨道系统动力特性及减振效果试验研究[J].中国铁道科学，2010（2）.

[8]Colorni A，Dorigo M，Maniezzo V，et al.Distributed optimization by ant colonies[C]//Proc of the 1st European Conference on Artificial Life.Paris：Elsevier，1991：134-142.

[9]金浩，刘维宁.基于觅食-返巢机制连续域蚁群算法[J].计算机工程与应用，2012，48（1）：24-26.

[10]金浩，刘维宁.多目标觅食-返巢机制连续域蚁群算法[J].计算机应用研究，2012，29（11）：4038-4040.

[11]UIC.对于有关铁路车辆振动中评估乘客乘坐舒适性的指导[S].1994.

[12]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.机械振动与冲击人体暴露于全身振动的评价第1部分：一般要求[S].2007.

[13]国家环境保护局.城市区域环境振动标准[S].1988.

[14]金浩，刘维宁.基于蚁群算法梯式轨枕轨道减振优化研究[J].中南大学学报：自然科学版，2012，43（7）.

JIN Hao1,LIU Weining2

1.College of Civil Engineering,Shaoxing University,Shaoxing,Zhejiang 312000,China
2.School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China

In order to optimize rail vibration acceleration and foundation vibration acceleration for the ladder track, MO-FHACO（multi-objective foraging-homing ant colony algorithm）is employed in this paper.The ladder track is simplified using four-pole parameter method.Vibration acceleration level of rail and vibration acceleration level of foundation ranging from 1 Hz to 80 Hz are set objective functions.Stiffness and number of sleeper bearings are set designing variables. After several optimizations by MO-FHACO,optimization solutions of bi-objective for the ladder track are obtained.Results show that,it’s an efficient method for multi-objective optimization of the ladder track with MO-FHACO.

ladder track;ant colony optimization algorithm;multi-objective;four-pole parameter method

鉴于梯式轨道在实际应用过程中，需要同时优化钢轨振动加速度和道床振动加速度，利用MO-FHACO（多目标觅食-返巢机制连续域蚁群算法）对其进行双目标优化。利用四端参数法建立对应的梯式轨道数学模型，将1～80 Hz频段钢轨振动加速度级和道床振动加速度级作为优化目标，枕下减振垫刚度和数量作为设计变量。经过MO-FHACO双目标优化，成功得到梯式轨道双目标优化解。结果表明，采用MO-FHACO对梯式轨道进行多目标优化具有工程应用价值。

梯式轨道；蚁群优化算法；多目标；四端参数法

A

TP39；U213.2

10.3778/j.issn.1002-8331.1404-0002

JIN Hao,LIU Weining.Multi-objective optimization for ladder track based on improved ant colony algorithm. Computer Engineering and Applications,2014,50（22）：28-31.

国家自然科学基金（No.51278043）。

金浩（1986—），男，博士，讲师，主要研究方向为轨道减隔振措施优化研究；刘维宁（1960—），男，博士，教授，主要研究方向为地下铁道运营环境影响。E-mail：jiaodajinhao@gmail.com

2014-04-01

2014-06-03

1002-8331（2014）22-0028-04

CNKI网络优先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1404-0002.html