基于离群特征模式的股市波动预测模型

王浩，陈娟，姚宏亮，李俊照

合肥工业大学计算机与信息学院，合肥 230009

基于离群特征模式的股市波动预测模型

王浩，陈娟，姚宏亮，李俊照

合肥工业大学计算机与信息学院，合肥 230009

随着金融市场的逐步完善，投资理念的逐步深入，股票投资被越来越多的人所接受，但是证券市场是高风险与高收益并存的，因此，有效的预测方法对减少投资风险是很有必要的，关于证券市场的分析和预测也一致为人们所关注。对于股票市场的预测问题国内外很多学者都做了有意义的探索，早期ARIMA技术应用于时间序列预测，但是ARIMA是线性预测的方法。随着非线性科学的发展，人们提出了神经网络方法应用在金融时间序列的分析和预测[1]，相对于ARIMA模型神经网络模型有很大的优势，然而神经网络方法有很多局限性，神经网络存在有很多参数如网络大小、初始权重的选择问题，而且可能存在过学习的现象，导致泛化能力很低，在训练过程中存在局部极小问题，且收敛速度慢。

支持向量机（Support Vector Machines，SVM）[2]已经被认为是先进的回归和分类的技术。最早是由Cortes和Vapnik于1995年提出，以统计学习理论为基础，其与传统机器学习理论最大的不同在于，它服从结构风险最小化原理而非经验风险最小化。SVM综合考虑经验风险与置信风险，具有很好的泛化能力。支持向量机可以获得全局最优，解决了其他的神经网络模型陷入局部最优的问题，而且支持向量机还能解决过度拟合的问题，很多的实验结果也表明SVM算法优于人工神经网络的预测[3]。

随着上市公司越来越多，股票市场的规模也越来越大，由于一支股票会受到诸多因素的影响，信息量是很庞大的，而且存在冗余，如果不对这些信息进行约减，会导致运算量很大，增加运算的时间。特征选择[4]是从原始的输入变量中挑选子集，选择的子集能更好地表示原数据集的特征，提高预测的精度和有效性。人们一直都在寻找快速、准确的约减算法，出现了很多关于特征选择的算法，基于核主成分分析作为特征选择预测股票价格[5]，将粗糙集与SVM结合进行特征选择[6]，GA遗传算法进行特征提取[7]等，但是这些算法有它们的局限性，没有从整个网络的角度考虑，目标变量的马尔可夫毯[8]与其他变量独立，屏蔽其他变量的影响，能较好地保证信息的独立性和完整性。

股市波动是一种必然现象，但由于中国股市容易受到的政府政策的影响，波动过于频繁和剧烈，相比其他成熟市场存在更多的异常波动，频繁且剧烈的波动会使投资者难以做出正确的投资决策[9]。股市的政策指标分为中长期连续性政策和短期性的离散政策事件，分析不同的政策对股市的冲击大小，结果表明连续性政策与我国股市之间存在正相关关系，但解释程度较小，股市的波动受短期性的政策时间影响较大，但政策事件对股市的冲击力在逐步减弱，股票市场也趋于成熟。而股票市场也有其自身的变化趋势，我们通过描述股票走势的指标从微观的角度去研究股票市场内部的波动现象，有很多学者分析技术指标对股票走势的影响[10-11]，离群特征模式针对股票中背离特征，将特征进行一定的组合提取，相比于其他的算法只是将特征作为模型的输入向量要更加合理、有效。

一种融合离群特征模式的支持向量机模型通过马尔可夫毯算法找出与目标结点相关的股票，对相关股票建立支持向量机模型，实验发现建立的模型对股票的一般波动预测效果比较好，对于异常波动不能得到有效的预测，进一步通过股票的指标特征与走势背离的现象提取特征模式，通过时序滑动窗口动态捕捉背离指标，将离群特征模式作为先验知识[12]加入原SVM模型中，可以减小异常波动带来的误差，提高模型的预测精度。

1 马尔可夫毯的相关概念

在给定的贝叶斯网络中（Bayesian networks）[13]中一个变量的马尔可夫毯时，贝叶斯网络中其他变量与该变量条件独立，一个变量的马尔可夫毯能屏蔽其他变量对该变量的影响。

定义1对贝叶斯网络G=＜V,E＞和联合概率密度P(V)，如果G所表示的条件独立性和P所表示的马尔可夫条件一一对应，称G和P是faithful。而在具有忠实性的因果概率网络中，任何变量的马尔可夫毯MB（T）是唯一存在的。

定义2 D-分离（D-separation）对于一个有向无环图，有三个互不相交的结点子集A、B、C，若A中一个结点X与B中一个结点Y之间的一条通路不满足以下两个条件：

（1）每一个具有汇聚结点的箭头的结点均在C中，或有一个子孙结点C中。

（2）其他所有结点都不在C中，称结点X和结点Y被集合CD-分离；能D-分离结点X和结点Y的最小结点集称为结点X和结点Y最小D-分离集。

定义3一个变量的马尔可夫毯MB(T)，是在给定集合时，变量集V中所有其他结点与变量T条件独立性最小的集合。在具有忠诚性的有向无环图中每个结点T的马尔可夫毯是由T的父结点、子结点、子结点的父结点组成。

图1是一个贝叶斯网络，图中所有结点均为结点X的马尔可夫毯，U1、Um为X的父结点，Y1、Ym为X的子结点，Z1、Zm为X的子结点的父结点，都是X结点的马尔可夫毯。

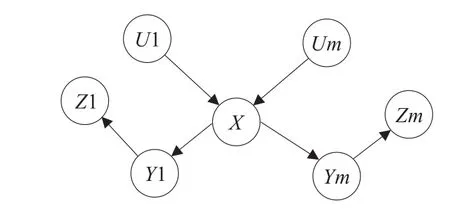
图1 贝叶斯网络

2 支持向量机算法介绍

支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的，在模型的复杂性和学习能力之间寻求最佳的折衷来获得更好的泛化能力。早期提出这个方法是为了解决模式识别分类问题，现在支持向量机已扩展到解决回归估计，并在时间序列预测，非线性建模和优化控制等问题上都有很好的应用。

支持向量机的基本思想是通过核函数将输入的变量映射到高维空间中，在新的特征空间进行线性回归。给定训练样本集(x1,y1),(x2,y2),…,(xl,yl)，其中xi∈RN为N维特征向量，yi∈{-1,1}或yi∈{1,2,…,k}；当yi∈{-1,1}时为最简单的二分类，当yi∈{1,2,…,k}为k分类问题。

在线性可分的情况下，存在一个超平面方程为w·x+b=0，对它进行归一化，线性可分的样本集满足yi((w·x)+b)-1≥0，i=1,2,…,l；分类间隔为2/||w||，要求最优超平面就要是分类间隔最大，εi是松弛变量表示被错分的程度，C是惩罚因子，表示加载错分点上的惩罚。原始的求解问题就转化为求解如下的凸二次规划问题：

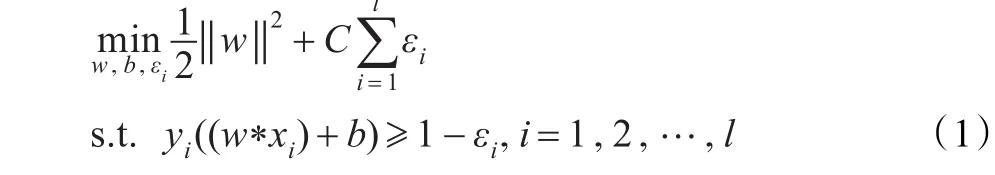
这是一个凸二次规划问题可以求得全局最优点，用Lagrange乘子把它转化成对偶形式来求解。得到最优超平面决策函数

对于非线性SVM的情况，是根据核函数将样本空间映射到高维的特征空间进行线性划分，为了避免高维特征中的复杂计算，支持向量机采用核函数K(xi·x)来代替高维空间中的内积运算。最优超平面的决策函数变为：

3 离群特征模式

一般情况下股票价格变化可以看作为一种光滑、连续的过程，这时股票市场稳定运行，投资者与股票发行方都可以进行正常的投资与经营活动，获得各自的收益。但在一些特殊情况（如国家重大经济政策的调整，各股票相关行业中发生突发事件以及投资者心态出现剧烈变化等情况）下，股票价格的短期变化将有可能由连续变化转化为跳跃式变化，这种由于宏观政策引起突变性是很难预测到的。

在股市预测中这种突变带来的尖峰点是造成误差的很大原因，针对这一情况引入离群特征，所有事情发生都有其前兆，事后从宏观方面看这种突变是具有可解释的，在事件发生之前从微观的角度可以发现某些端倪的。这种离群特征是股市微观层面的一些指标，像成交量，换手率，包括一些K线指标，这些指标是对股市的一种刻画，当两者发生背离时预测走势即将发生改变，根据特征背离的情况提取离群特征模式【14】。

3.1 离群特征模式定义

定义4（离群特征模式）股票指标是运用一些复杂的数学公式，用数据来论证股票趋向、买卖的分析方法的一种工具。背离有两种情况，一种是指标与走势发生背离；一种是指标之间发生背离。股票数据D={S1,S2,…,Sn}，其中Si是第i支股票的数据，Si={Yt,k1,k2,…,km}，Yt记录的是股票的收盘价，k1,k2,…,km记录股票的一些指标包括成交量、MACD、KDJ等K线指标。

（1）指标k1,k2,…,km，收盘价为Yt，如果f(k1,k2,…,km)*Yt＜0指标组合与走势发生背离，Yt+1=F(f(k1,k2,…,km),Y)，后一天的走势是指标组合与前面走势的一个函数。指标与股票的走势是相关的，如果两者之间发生背离，说明走势即将发生大的变化。

（2）指标k1,k2,…,km，fi(k1,k2,…,km)*fj(k1,k2,…,km)＜0，指标之间发生背离，也是一种异常情况。

本文主要考虑的是指标与走势之间的背离关系，根据指标与走势的背离情况提取的指标组合构成一个模式，称为离群特征模式。

3.2 离群特征模式提取

根据股票价格时序数据的K线指标分析，根据走势的异常波动对K线指标的背离情况进行离群特征提取，提取了三种背离特征模式，并且用案例对提取的模式进行了论证。

案例一（房地产板块）2012年12月24日上涨0.8%，成交量明显缩量，12月25日上涨4.24%；2012年12月4日上涨缩量，12月5日是长阳，涨幅达3.03%。

案例二（上证指数）2012年1月6日上涨0.7%，成交量缩量，1月7日上涨2.89%；2010年12月10日上涨1.07%成交量缩小，12月11日上涨2.88%。

定义6（MACD背离）在震荡后期，观察MACD指标在震荡期间正能量柱不断缩短（负能量柱不断增长），观察KDJ指标也在下降，尤其是当KDJ出现死叉，MACD指标Mt，KDJ指标Kt、Dt、Jt，当Mt-Mt-1＜0 AND((Kt-Dt)＜εAND(Jt-Dt)＜εAND(Jt-Kt)＜ε))，说明后面已经缺乏能量提供股价继续上涨，股价下跌。

案例三（房地产板块）2013年1月4日开始有连续5天的震荡，在第五天上涨的时候能量柱还是在下降，指标发生背离，KDJ指标形成死叉，1月11日跌幅3.38%；2012年9月10日震荡5天，第四天能量柱开始下降，KDJ形成死叉，第五天小幅上涨跟指标发生背离，9月17日跌幅3.74%。

案例四（上证指数）2012年8月7日由连续的小幅涨跌，第四天下跌但MACD能量柱继续上涨，KDJ开始下跌，8月31日开始下跌；2011年7月14日开始小幅震荡，第7天十字星形式的上涨，MACD继续下跌，KDJ也一直在下跌，7月25日下跌2.96%。

突变的长实体打破了之前的走势，影响后面的预测，尤其是长实体之后又出现长实体（双实体），之前建立的模型很难立即跟上这样的变化趋势进行预测，而且这种突变本身就带有很多的信息，不是每次都可以及时捕捉到有效信息去预测变化，在出现突变之后捕捉有效的特征提取模式。

案例五（房地产板块）2012年12月28日上涨2.76%，成交量是前一天的1.2倍，12月31日上涨2.18%；2012年6月6日上涨2.13%，成交量是前一天1.2倍，后面连续小幅上涨3天。

案列六（上证指数）2012年9月27日上涨2.60%，成交量是前一天1.4倍，28日上涨1.45%；2012年2月8日上涨2.43%，成交量是前一天1.3倍，之后连续小幅上涨两天。

4 融合离群特征模式的支持向量机

本文提出一种融合离群特征模式的支持向量机算法，由于股票之间是相互关联的，相互之间有信息传递，也会互相影响，在给定目标变量的马尔可夫毯的情况下，目标变量和网络中的其他变量是条件独立的，从而能得到与目标变量关联性较强的局部变量集合，这种局部变量可以屏蔽其他变量的影响，保证信息的完整性；一支股票除了会受到其他股票的影响，自身的一些信息也有一定的意义，根据目标变量的相关数据提取离群特征模式作为先验知识[15]，用时序滑动窗口捕捉离群特征，建立离群特征模型，可以有效地预测由背离引起的异常波动。该算法从两个角度出发进行股票的预测，将两个模型融合在一起，能有效地提高预测精度。

4.1 马尔可夫毯进行特征选择

在股票市场中各个股票相互之间是有关联的，马尔可夫毯算法可以屏蔽网络中其他结点对目标变量的影响。本文用的是HITON_PC/MB算法【16】，这个算法是当前主要学习马尔可夫毯的算法，首先启发式搜索与目标结点T关联性最强的结点，用条件独立性测试得到目标结点T的父结点和子结点的集合PC(T)，再次调用算法，可以得到结点T父结点的父结点，父结点的子结点，子结点的父结点，子结点的子结点集合PC(PC(T))，再根据条件依赖的性质寻找配偶结点，剔除与T不互为父子的结点，从而获得目标结点T的马尔可夫毯集合MB(T)。

4.2 建立离群特征模型

一支股票不仅受到其他相关股票的影响，股票自身反映走势的指标也会对股票走势的预测带来很多有价值的信息。离群特征模式中定义的三种背离模式，不是直接将这些特征作为输入变量，而是对特征进行一定的提取。上涨背离主要收集的特征是成交量与前一天成交量的差值，成交量与平均成交量的差值；MACD背离收集的指标是股票涨跌与能量柱上下波动趋势的对比，计算背离的大小，以及KDJ的变化趋势，将这些特征k1,k2,…,km进行特征组合后的特征变量f1(k1,k2,…,km),f2(k1,k2,…,km),…,fn(k1,k2,…,km)作为支持向量机的输入变量，收益率U(i)为输出变量，建立离群特征模型。

4.3 离群特征模式的引入

使用时序滑动窗口捕捉离群特征，将离群特征模型预测的结果作为先验知识加入SVM模型中，在支持向量机公式中加入约束条件使预测结果在[U(i)+μ1,U(i)-μ2]范围之间，μ1、μ2参数通过建立离群特征模型的误差获得。

类似标准的支持向量机算法，融合先验知识的支持向量机表示：

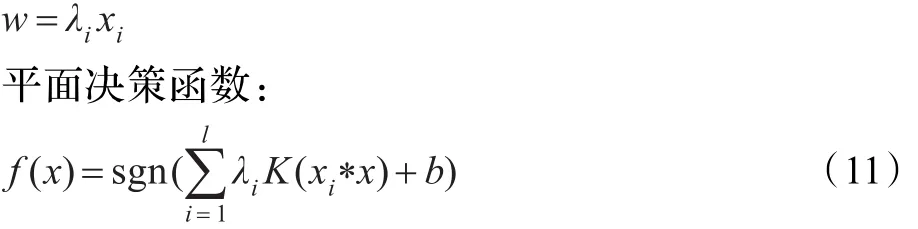
4.4 算法描述

输入：股票价格数据集Data1，股票特征集Data2

输出：预测股票收益率结果

步骤1用公式Ri(t)=ln(Ii(t)/Ii(t-1))将股票价格转化为收益率。

步骤2用HITON_PC/MB算法获得目标变量T的马尔可夫毯mb。

步骤3将目标变量T以及马尔可夫毯mb的收益率作为支持向量机的输入变量，建立基本的支持向量机模型。

步骤4根据定义的离群特征模式对特征k1,k2,…,km进行组合，将组合后的特征变量f1(k1,k2,…,km),f2(k1,k2,…,km),…,fn(k1,k2,…,km)作为支持向量机的输入变量，建立离群特征模型，用训练数据建立的模型去预测训练数据，求得平均误差值为μ1、μ2的大小。

步骤5使用时序滑动窗口捕捉离群特征，如果存在离群特征使用离群特征模型预测，将预测结果作为原SVM模型的先验知识，进行条件约束。

步骤6预测结果评价。

5 实验数据处理

5.1 本文数据来自大智慧软件下载的上证行业板块指数

第一组数据采用的是30个板块自2008年12月24日至2012年7月10日交易日股票行业板块每日收盘指数，一共是860个数据。

表130 个板块的名称

5.2 用马尔可夫毯进行特征选择

本文采用收盘指数的日对数收益率作为股市行业板块的指标，日对数收益率是指当日的收盘价格比上昨日的收盘价格的值取对数，用Yt表示板块i在日期t的收盘价格，Ri(t)=lnln(Yt/Yt-1)表示板块t在日期t的日对数收益率。

以1号结点房地产板块为目标变量，马尔可夫毯学习算法——HITON_PC/MB算法目标变量的马尔可夫毯，1号结点是（房地产）的马尔可夫毯是5（银行）、15（旅游酒店）、19（建材）、25（工程建筑）、30（电力）。

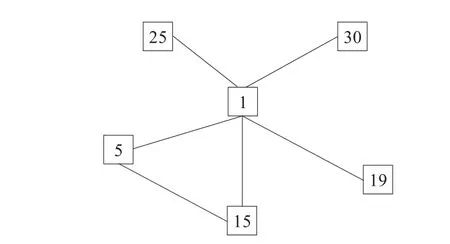
图2 结点1（房地产板块）的马尔可夫毯

5.3 对数据预处理

对于一个m维的样本数据，如果不同分量的数据在不同的数量级上，数量级大的分量就会掩盖数量级小的分量的影响，所以对原始数据要进行一定的处理。对与不同分量中那个每一个值都减去该分量的最小值，再除以该分量最大值与最小值之差。

5.4 模型参数的选择

对于内积核函数的选择，目前最常用的主要有线性核函数，多项式核函数，高斯径向基核函数，但实验研究表明采用这三种不同核函数的SVM能得到性能相近的结果，且支持向量的分布差别不大。本文使用的核函数是最常用的径向基核函数。本文采用交叉验证和网格搜索方法对参数C，g寻优，参数C是惩罚参数，参数g是RBF可函数中的参数g，让C、g在一定范围内取值，使用交叉验证的方法，最终取在训练集上误差最小的参数值作为最优参数，过高的C会导致过学习现象的发生，搜索到的最小误差所有的成对C、g中，选择惩罚参数最小的C作为最佳的对象。

5.5 对比实验算法

关于对比实验算法部分使用两个对比算法，一个使用标准的支持向量机算法，以成交量指标作为算法的输入向量；另一个使用BP神经网络算法。

5.6 评价标准

均方误差：

N表示预测集的样本个数，y是真实值，y′是预测值，MSE，MAE用来表示预测值偏离实际值的大小，它的值越小表明偏离度越小，说明预测结果的精确度越高。

6 支持向量机预测的结果分析

6.1 数据选择

表2 收集数据分成四组进行实验

6.2 离群特征模式SVM算法与以成交量作为输入变量SVM对比

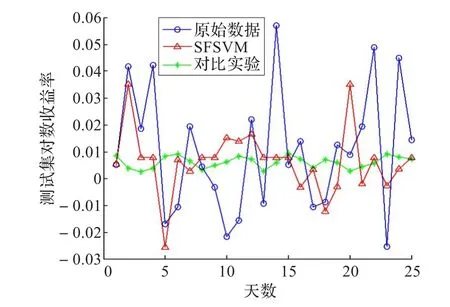
图3 数据D-I进行实验对比图

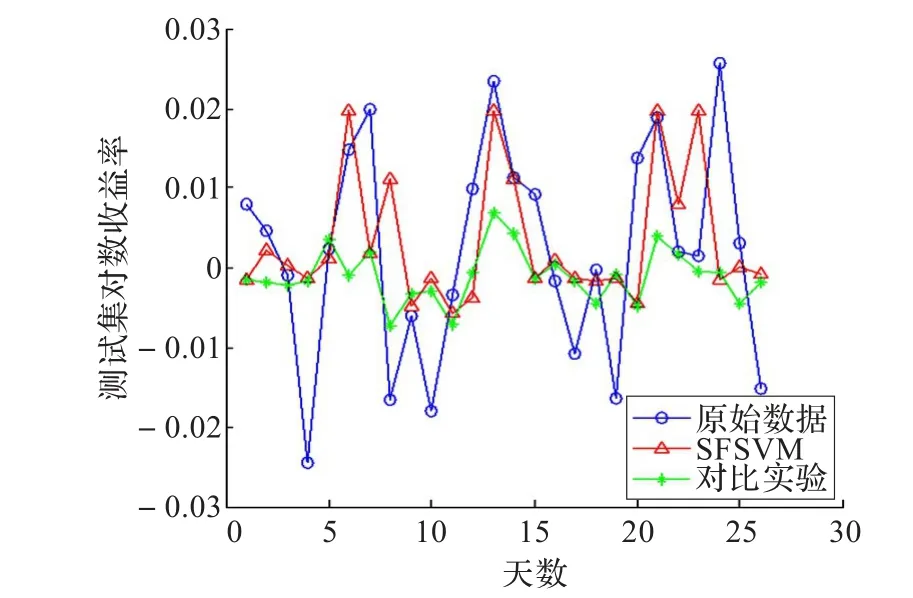
图4 数据D-II进行实验对比图

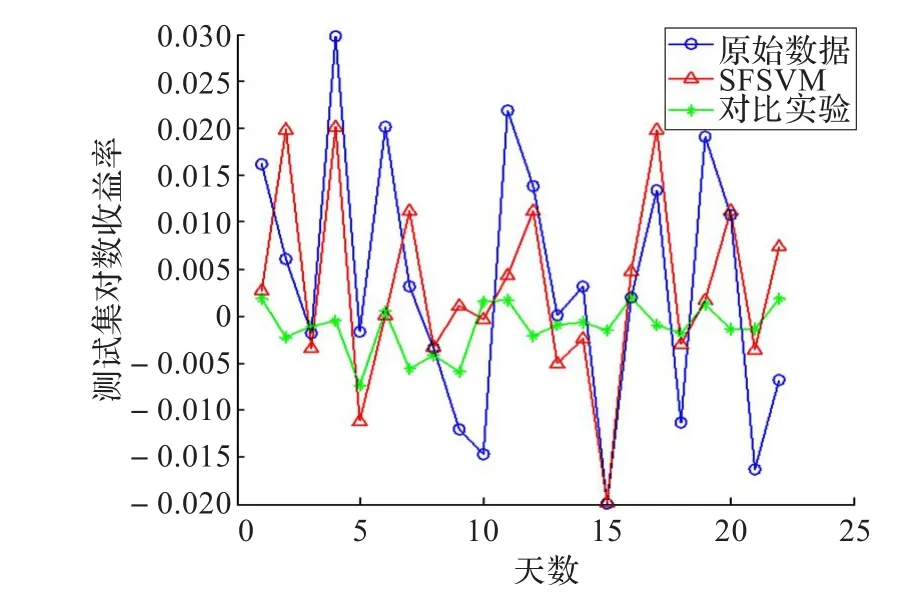
图5 数据D-III进行实验对比图

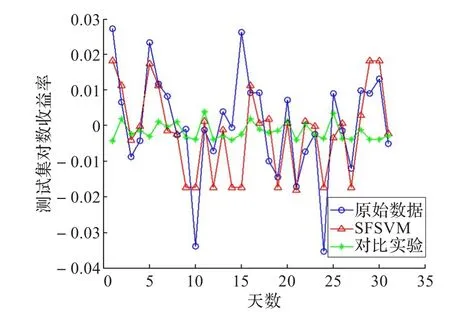
图6 数据D-IV进行实验对比图

6.3 离群特征模式SVM算法与BP神经网络对比

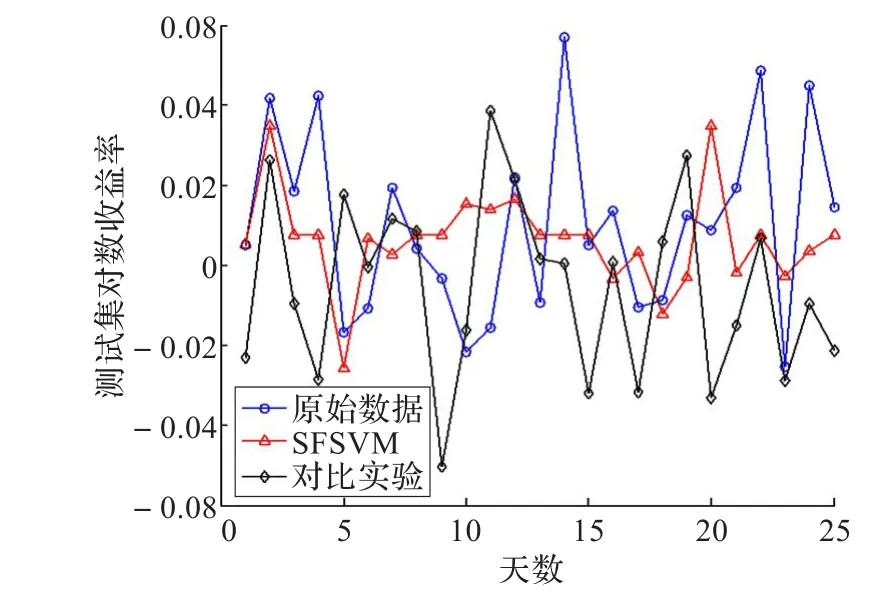
图7 D-I数据进行实验对比图

图8 D-II数据进行实验对比图

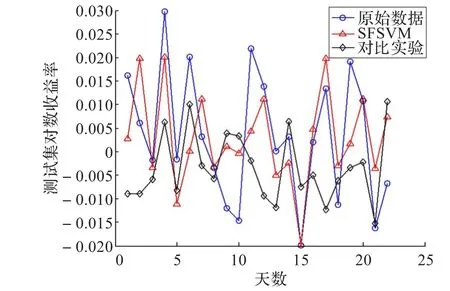
图9 D-III数据进行实验对比图

6.4 结果分析

根据上面两个对比算法分析的图形可以看出，SFSVM算法对于一部分股票走势的尖峰点有一定的预测，在数据D-I中SFSVM算法对数据中第2，3，18点相对于对比算法有比较好的预测效果，第2，3点出现上涨背离，第2个点前一天的缩量上涨，第3个点前一天大幅上涨成交量上涨不明显，第18个点出现MACD背离，前一天在下降但MACD指标上升，KDJ指标也在下降；在数据D-II中SFSVM算法对数据中第6，13，14，22点有比较好的预测效果，6，13，22这三个点都是前一天的上涨缩量，第14点是前一天大幅上涨成交量上涨不明显；在数据D-III中SFSVM算法对数据中4，12，15，17，20这五个点有比较好的预测效果，第4个点是MACD背离，12，20这两个点是大幅上涨成交量不明显，15，17这两个点上涨缩量；在数据D-IV中SFSVM算法对数据中1，2，5，6，30这5个点有比较好的预测结果，1，30是上涨缩量背离，第5点是MACD背离，2，6是大幅上涨出现背离。

表3 误差结果

图10 D-IV数据进行实验对比图

对这四段数据分别进行预测结果分析，SFSVM算法对于大幅波动的股票走势预测有一定的效果，虽然SFSVM算法会在某些情况下判断失误造成误差，但根据表3的误差总体结果可以看出SFSVM在一定程度上优于两种比较算法，能有效减少误差。

7 结束语

本文提出一种离群模式的支持向量机算法（SFSVM）用马尔可夫毯进行特征选择，选择出与目标板块相关的其他板块，再根据股票的内部指标信息提取离群模式作为先验知识，将不同的方面结合在一起提高整体的性能。从实验图形中可以看出该算法对股市中的某些异常突变点是可以提前感知的，但由于中国股市受经济政策影响比较大，有些突变点很难预测的，预测的结果和实际也是有很大偏差的。总体来说，根据实验分析，对比其他算法该算法，有更好的预测效果。

[1]Hill T，O’Connor M，Remus W.Neural network models for time series forecasts[J].Management Science，1996，42：1082-1092.

[2]Vapnik V.The nature of statistic learning theory[M].New York：Springer，1995.

[3]Tay F E H，Cao L.Application of support vector machines in financial time series forecasting[J].Omega：The International Journal of Management Science，2001，29：309-317.

[4]Tsamardinos，Aliferis C F.Towards principled feature selection：Relevancy，filters and wrappers[C]//Ninth International Workshop on Artificial Intelligence and Statistics（AI&Stats 2003），2003.

[5]Cao L J，Chua K S，Guan L K.Combining KPCA with support vector machine for time series forecasting[C]//Proceedings of IEEE International Conference on Computational Intelligence for Financial Engineering，2003：325-329.

[6]Zhang T，Sai Y，Yuan Z.Research of stock index futures prediction model based on rough set and support vector machine[C]//Proceedings of the IEEE International Conference on Granular Computing，Hangzhou，China，2008：797-800.

[7]Huang Shian-Chang，Wu Tung-Kuang.Integrating GA-based time-scale feature extractions with SVMs for stock index forecasting[J].Expert Systems with Applications，2008，35：2080-2088.

[8]Pearl J.Probabilistic Reasoning in Intelligent Systems[M]. [S.l.]：Morgan Kaufmann，1988.

[9]徐君华，李启亚.宏观政策对我国股市影响的实证研究[J].经济研究，2009（9）：12-21.

[10]Wang Xiaoyun，Lin Limin.Short-term prediction of Shanghai composite index based on SVM[Z].2010.

[11]常冶衡，袁芳.基于技术分析指标解析中国股市[J].中国证券期货，2010（10）.

[12]Lauer F，Bloch G.Incorporating prior knowledge in support vector machines for classification.A review[J].Neurecomputing，2008，71（7/9）：1578-1594.

[13]Ronan D.Learning Bayesian networks：Approaches and issues[J].Knowledge Engineering Review，2011，26（2）：99-157.

[14]薛安荣，姚林，鞠时光，等.离群点挖掘方法综述[J].计算机科学，2008，35（11）：13-18.

[15]Lauer F，Bloch G.Incorporating prior knowledge in support vector machines for classification：A review[J].Neurocomputing，2008，71（7）：1578-1594.

[16]Aliferis C F，Tsamardinos I，Statnikov A.HITON：A novel Markov blanket algorithm for optimal variable selection[C]// American Medical Informatics Association Annual Symposium，2003.

WANG Hao,CHEN Juan,YAO Hongliang,LI Junzhao

School of Computer and Information,Hefei University of Technology,Hefei 230009,China

Due to the stock price fluctuations have stronger mutation and easily influenced by outside factors,cause it’s difficult to predict stock price movements.A stock market volatility forecasting model based on characteristics of outliers pattern（SFSVM）is presented.Firstly,SFSVM algorithm utilizes Markov Blanket algorithm obtaining local network to shield the effects of other node to the target node;Secondly,analyzing the index of the target node to extract characteristic of outliers pattern from the general behavior；then SFSVM algorithm capture outlier features using sliding window,put characteristic of outliers pattern into original SVM model as a prior knowledge,this method can predict peak point and smooth effect of peak point on the predicted results,it also can improve forecasting model robustness.Experimental results, obtained by running on datasets taken from stock plate index,show that this method performs better than neural network algorithm and the standard SVM algorithm on stock trend projections.

characteristics of outliers model;Support Vector Machines（SVM）;Markov Blanket;prior knowledge

由于股票价格波动具有较强的突变性且易受外界因素影响，导致股票价格走势难以预测。提出基于离群特征模式的股市波动预测模型（SFSVM）。该算法首先利用马尔可夫毯选取目标结点的局部网络结构，以屏蔽其他结点对目标结点的影响；对目标结点的指标进行分析，提取异于一般行为的离群特征模式；利用滑动窗口捕捉离群特征，将离群特征模式作为先验知识加入原SVM模型，预测尖峰点并平滑尖峰点对于预测结果的影响，提高预测模型的稳健性。在股票板块数据上进行实验结果证明，SFSVM算法相对于神经网络和标准的SVM算法，在股票的走势预测方面有更好的预测效果。

离群特征模式；支持向量机；马尔可夫毯；先验知识

A

TP18

10.3778/j.issn.1002-8331.1305-0154

WANG Hao,CHEN Juan,YAO Hongliang,et al.Stock market volatility forecasting model based on characteristics of outliers pattern.Computer Engineering and Applications,2014,50（22）：243-249.

国家自然科学基金（No.61175051，No.61070131，No.61175033）。

王浩（1962—），教授，中国计算机学会高级会员，研究方向：人工智能；陈娟（1989—），硕士，研究方向：人工智能和知识工程；姚宏亮（1972—），男，博士，副教授，计算机学会会员，研究方向：人工智能和知识工程；李俊照（1975—），博士研究生，讲师，研究方向：机器学习与人工智能。

2013-05-14

2013-09-03

1002-8331（2014）22-0243-07

CNKI网络优先出版：2013-09-04.,http://www.cnki.net/kcms/detail/11.2127.TP.20130904.1344.017.html