不确定线性系统新的稳定性准则

廖慧敏，谭满春

暨南大学数学系，广州 510632

不确定线性系统新的稳定性准则

廖慧敏，谭满春

暨南大学数学系，广州 510632

1 引言

时滞现象经常存在于网络控制系统、自动化系统、通信系统、运输系统等许多动态系统中。由于时滞会导致系统的不稳定性和性能变差，因此时滞的稳定性得到了广泛的关注[1-25]。

为得到时滞系统的稳定性准则，许多学者提出了不同的方法[1-12]。文献[1-2]通过引入自由权矩阵来处理Lyapunov函数导数中的相关项，优势在于不必对交叉项进行处理，但引入过多的变量会增加计算的复杂度。文献[3-4]采用Jensen积分不等式对交叉项进行放大处理。文献[5-6]构造含有三重积分项的新型Lyapunov函数，并结合积分不等式法或自由权矩阵方法。文献[7-8]利用时滞中点法，用时滞区间的中点(h1+h2)/2把时滞区间分割成相等的两个区间，再充分利用积分不等式等方法。

基于上述研究成果，本文不同于文献[7-8]，不再把时滞分割成相等的两区间，而用分割点h=λh1+(1-λ)h2将时滞区间分割成任意两段。通过构造新的Lyapunov函数，并结合积分不等式，得到了新的稳定性准则。本方法引入了状态向量x(t-h)，含有更多的时滞区间信息。通过数值实例说明本文方法的有效性和较小的保守性。

本文符号说明：I表示单位矩阵，Rn表示n维欧式空间，Rn×m表示n×m矩阵，T表示矩阵转置，*表示矩阵相应的对称部分，对任意矩阵A,B,A＞B表示矩阵A-B是正定矩阵。

2 问题描述

考虑如下不确定系统：

本文定理证明将用到如下引理：

3 主要结果

备注1系统最大允许时滞上界的大小与λ的精度有关。假设λ的精度为0.01，由于0＜λ＜1，那么λ的值是0.01，0.02，…，0.99。把每个λ的值作为已知数，由上述定理，利用MATLAB的LMI工具箱，可以求得相应的最大允许时滞上界，取这些最大允许时滞上界的最大值做为系统的最大允许时滞上界。为求得更大的系统最大允许时滞上界，可以提高λ的精度，但这样会增加计算的复杂度，需要更多的计算时间。

4 数值实例

例1考虑具有如下系数矩阵的不确定线性系统：

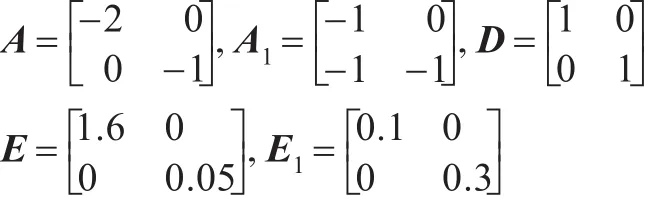
当假设λ的精度为0.1。当h1=0时，对不同的时滞变化率d，系统式（1）最大允许时滞上界h2值见表1。当d=0.1时，文献[15]的最大允许时滞上界为1.107 5,而由定理1，令λ=0.5，计算得到最大允许时滞上界为1.178 2。由表1知，与文献[14-15]相比，本文方法具有较小保守性。

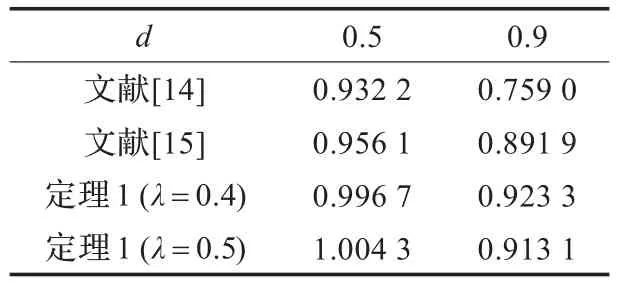
表1 h 1=0时，对不同d的最大允许时滞上界

例2考虑具有如下系数矩阵的不确定线性系统：

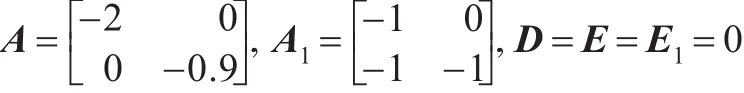
假设λ的精度为0.01。当d=0.5,h1=0时，由定理1，系统式（1）在λ=0.55时取得系统的最大允许时滞上界h2=2.194 0。当d=0.5,h1=1时，系统式（1）在λ=0.31时取得系统的最大允许时滞上界h2=2.279 2，见表2。当d=0.2,h1=0时，系统在λ=0.48时取得最大允许时滞上界为3.293 6，见表3。由表2，3可知，在h1较小的情况下，与文献[7-8]相比，本文方法具有较小保守性。

表2 d=0.5时，对不同h1的最大允许时滞上界

表3 d=0.2,h1=0时，最大允许时滞上界

5 结论

本文研究了带有区间时滞的不确定线性系统的稳定性问题。利用时滞分割法，通过构造适当Lyapunov函数，并结合积分不等式，得到了不确定线性系统新稳定性的准则。数值实例表明，新的稳定性准则具有更小的保守性。

[1]Qiu Fang，Cui Baotong，Ji Yan.Further results on robust stability of neutral systems with mixed time-varying delays and nonlinear perturbations[J].Nonlinear Analysis：Real World Applications，2010，11（2）：895-906.

[2]Liang Yuanxin.Robust stability for uncertain neutral systems with time-varying and distributed delays[C]//Seventh International Conference on Computational Intelligence and Security，2011：321-324.

[3]Sarabi F E，Momeni H R.Less conservative delay-dependent robust stability criteria for linear time-delay systems[C]// International Conference on Electronics Computer Telecommunications and Information Technology，2010：738-741.

[4]Ramakrishnan K，Ray G.Robust stability criteria for uncertain linear systems with interval time-varying delay[J].J Control Theory Appl，2011，9（4）：559-566.

[5]Sun Jian，Chen Jie，Liu G P.Delay-range-dependent and rate-range-dependent stability criteria for linear systems with time-varying delays[C]//Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference，Shanghai，China，2009：251-256.

[6]Sun J，Liu G P，Chen J，et al.Improved stability criteria for linear systems with time-varying delay[J].IET Control Theory Appl，2010，4（4）：683-689.

[7]Peng C，Tian Y C.Improved delay-dependent robust stability criteria for uncertain systems with interval timevarying delay[J].IET Control Theory Appl，2008，2（9）：752-761.

[8]Zhao Xia，Song Jin，Tian Engang，et al.Delay-dependent stability analysis for linear system with time-varying delay：a PAM method[C]//Chinese Control and Decision Conference，2009：1422-1426.

[9]Zhang Ao，Xu Zhaodi，Liu Dong.New stability criteria for neutral systems with interval time-varying delays and nonlinear perturbations[C]//27th Chinese Control and Decision Conference，2011：2995-2999.

[10]Tan Manchun.Global asymptotic stability of fuzzy cellular neural networks with unbounded distributed delays[J]. Neural Processing Letters，2010，31（2）：147-157.

[11]Tan Manchun.Exponential convergence behavior of fuzzy cellular neural network with distributed delay and timevarying coefficients[J].International Journal of Bifurcation and Chaos，2009，19（7）：2455-2462.

[12]Tan M C，Su Z Y.Exponential stability analysis of neural networks with variable delays[J].International Journal of Bifurcation and Chaos，2010，20（5）：1541-1549.

[13]Guo Liangdong，Gu Hong，Jun Xing，et al.Asymptotic and exponential stability of uncertain system with interval delay[J].Applied Mathematics and Computation，2012，218（19）：9997-10006.

[14]Peng C，Tian Y C.Delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J]. JournalofComputationalandAppliedMathematics，2008，214（2）：480-494.

[15]Wang Cheng，Shen Yi.Improved delay-dependent robust stability criteria for uncertain time delay systems[J]. Applied Mathematics and Computation，2011，218（6）：2880-2888.

[16]He Y，Wang Q，Lin C G，et al.Delay-range-dependent stability for systems with time-varying delay[J].Automatica，2007，43（2）：371-376.

[17]Shao Hanyong.New delay-dependent stability criteria for systems with interval delay[J].Automatica，2009，45（3）：744-749.

[18]Kwon O M，Park M J，Park J H，et al.New delay-partitioning approaches to stability criteria for uncertain neutral systems with time-varying delays[J].Journal of the Franklin Institute，2012，349（9）：2799-2823.

[19]Qiu Fang，Cui Baotong，Ji Yan.A delay-dividing approach to stability of neutral systems with mixed delays and nonlinear perturbations[J].Applied Mathematical Modelling，2010，34（11）：3701-3707.

[20]Liu Pinlin.A delay decomposition approach to robust stability analysis of uncertain systems with time-varying delay[J].ISA Transactions，2012，51（6）：694-701.

[21]Chen Huabin.New delay-dependent stability criteria for uncertain stochastic neural networks with discrete interval and distributed delays[J].Neurocomputing，2013，101（4）：1-9.

[22]Ramakrishnan K，Ray G.Robust stability criteria for a class of uncertain discrete-time systems with time-varying delay[J].Applied Mathematical Modelling，2013，37（3）：1468-1479.

[23]Chen Huabin，Zhang Yong，Zhao Yang.Stability analysis for uncertain neutral systems with distributed delays[J]. Applied Mathematical and Computation，2012，218（23）：11351-11361.

[24]Xia Nan，Jia Yingmin.Delay distribution dependent stability criteria for interval time-varying delay systems[J]. Journal of the Franklin Institute，2012，349（10）：3142-3158.

[25]Zheng Min，Fei Minrui，Li Yang.Improved stability criteria for uncertain delayed neural networks[J].Neurocomputing，2012，98（3）：34-39.

LIAO Huimin,TAN Manchun

Department of Mathematics,Jinan University,Guangzhou 510632,China

The stability problem for uncertain linear systems with interval time-varying delay is studied.Based on the delaydividing approach,the delay interval is partitioned into two subintervals.By constructing an appropriate Lyapunov function and using integral inequalities,some delay-dependent stability criteria are obtained.Numerical examples are given to illustrate the effectiveness of the results.

uncertain linear systems;Lyapunov function;delay-dependent;stability

研究了带有区间时滞的不确定系统的稳定性问题。通过采用时滞分割法，把时滞区间分割成任意两小段，并构造恰当的Lyapunov函数，利用积分不等式，得到了新的时滞相关的稳定性准则。通过数值例子验证了结果的有效性。

不确定线性系统；Lyapunov函数；时滞依赖；稳定性

A

TP13；O213.2

10.3778/j.issn.1002-8331.1212-0016

LIAO Huimin,TAN Manchun.New stability criteria for uncertain linear systems.Computer Engineering and Applications,2014,50（22）：256-259.

广东省自然科学基金（No.S201201001036）；广东省科学计划项目（No.2009B011400046）。

廖慧敏（1987—），男，硕士研究生，主要研究方向：系统优化与控制；谭满春（1968—），男，教授，硕士生导师，主要研究方向：系统优化与控制。E-mail：tanmc@jnu.edu.cn

2012-12-03

2013-02-18

1002-8331（2014）22-0256-04

CNKI网络优先出版：2013-03-13，http://www.cnki.net/kcms/detail/11.2127.TP.20130313.0950.011.html