三维装箱问题的偏随机密钥混合遗传算法

游伟，雷定猷，朱向

中南大学交通运输工程学院，长沙 410075

三维装箱问题的偏随机密钥混合遗传算法

游伟，雷定猷，朱向

中南大学交通运输工程学院，长沙 410075

1 引言

三维装箱问题（three-Dimensional Container Loading Problem，3DCLP）是指从多件货物中选择若干件货物经过适当的组合并按照一定的顺序装入某个集装箱中，以达到箱子容积和载重量最大化利用的目的。货物是具有一定的尺寸和质量的矩形、匀质类物品，箱子为具有矩形空间容积及一定承载能力的矩形容器。货物以正交的形式放入集装箱，摆放方向任意，最多包含6种旋转方向。由于物品和容器存在不同规格，不同货物组合及其摆放位置都将对装载效果带来不同影响，同时还要求满足装载稳定性、货物表面承载能力及重心平衡等约束条件，因而装箱问题属于复杂组合优化问题，具有NP难问题的特点[1]。

实现货物的高效装载及合理布局，在空运、海运及铁路等装运领域具有重要的意义，已吸引了一批学者对此优化问题进行研究，并总结出一整套求解方法，主要包括确定性方法、随机搜索和混合方法等三类方法。

确定性方法中，Chen[2]的整数规划、Hifi[3]的分支定界法是其中典型的代表，这些方法主要适合规模较小的装载问题。对于规模较大的问题，可采用随机搜索方法并结合启发式规则进行求解，包括使用遗传算法[4-5]、模拟退火算法[6]、禁忌算法[7-8]、贪婪随机自适应搜索[9]等随机搜索机制寻优，以实现在相对较大的空间范围内对解的搜索。

除上述典型的优化方法外，更多的研究是将启发式方法与随机搜索结合起来形成的混合优化方法。Gehring和Bortfeldt先利用“塔”集生成算法构造出各种塔型货物单元，再按照遗传算法搜索出的装载序列及BL（Best fit decreasing）规则进行装载[4]；Davies和Elye[10-11]基于货物层布局单元形成初始布局，再利用遗传算法实现层的旋转与货物重心位置的调整。

一般而言，以构造法为代表的启发式方法能根据问题的特点快速搭建起求解的框架，并以此作为问题求解的方向，但它一般只能达到局部最优，由于三维装载问题的复杂性，过多地依赖构造法来布局将使求出的解的质量受到影响；而随机优化算法能实现在相对较大的空间范围内的寻优，对获得全局优化解起到一定的保障，但搜索的时间长，效率一般，不及构造法。将构造法与随机算法有效结合起来形成的混合优化方法，能将两者的优点结合到一起同时弥补各自的不足，因而被广泛运用于装载布局优化问题的求解。本文采用启发式方法与遗传算法相结合的混合算法对铁路集装箱装载问题进行研究。

2 问题描述及数学模型

2.1 问题描述

对不同运输领域中的集装箱进行装载，要求实现的目标及需考虑的实践约束条件有所不同，本文主要针对铁路集装箱的装载布局进行研究。它是指从多件货物中选择若干件进行组合，以正交的形式装入一个集装箱，要求在满足有关实践约束的条件下，实现装载空间与负载能力利用最大化。集装箱在铁路上的装运经常需要考虑的约束中，除了集装箱空间容积与载重量约束以外，主要包括货物的集重与重心平衡等约束[12]。装载集重主要出现在装运重量较大、体积较小的集重类货物的条件下，本文研究一般类型货物的装运，不涉及该因素的讨论。进一步，对问题论述的前提作以下规定：

（1）装载的货物为长方体，质量均匀，摆放方向任意。

（2）货物及其包装良好，可支撑承重和多层装载，不是危险品等特殊货物。

（3）货物是同一到达站，不考虑中间加装或卸货的情形。

（4）使用一个集装箱装载，允许留下货物以后装载。

把形状和重量完全相同的货物称为同类货物，本文研究的装载布局模型可定义为：

多件N类长方体货物（每类各有n1,n2,…,nN件）用一个集装箱装运到同一目的地，要求满足下列约束条件的前提下，最大化集装箱装载空间与负载能力的利用。

（1）集装箱装载的货物互不干涉且不超出装载空间的边界。

（2）所装货物的重量和体积之和不超过其允许载重量和有效容积。

（3）集装箱装载的货物，其合重心的偏移量不超过容许的范围。

2.2 数学模型

以集装箱左后下角为坐标原点，底板为X-Y平面，建立空间直角坐标系：Y轴平行于箱子纵中心线，方向从左向右；X轴沿箱端，方向从后向前；Z轴垂直于底平面向上。设货物pij装箱后重心坐标为分别为货物重心到YZ平面、XZ平面和XY平面的距离，货物pij左后下角的坐标为(xij,yij,zij)。车辆底面中心坐标为(C1,C2,0)，根据上述设定，建立如下平衡装载优化布局数学模型：

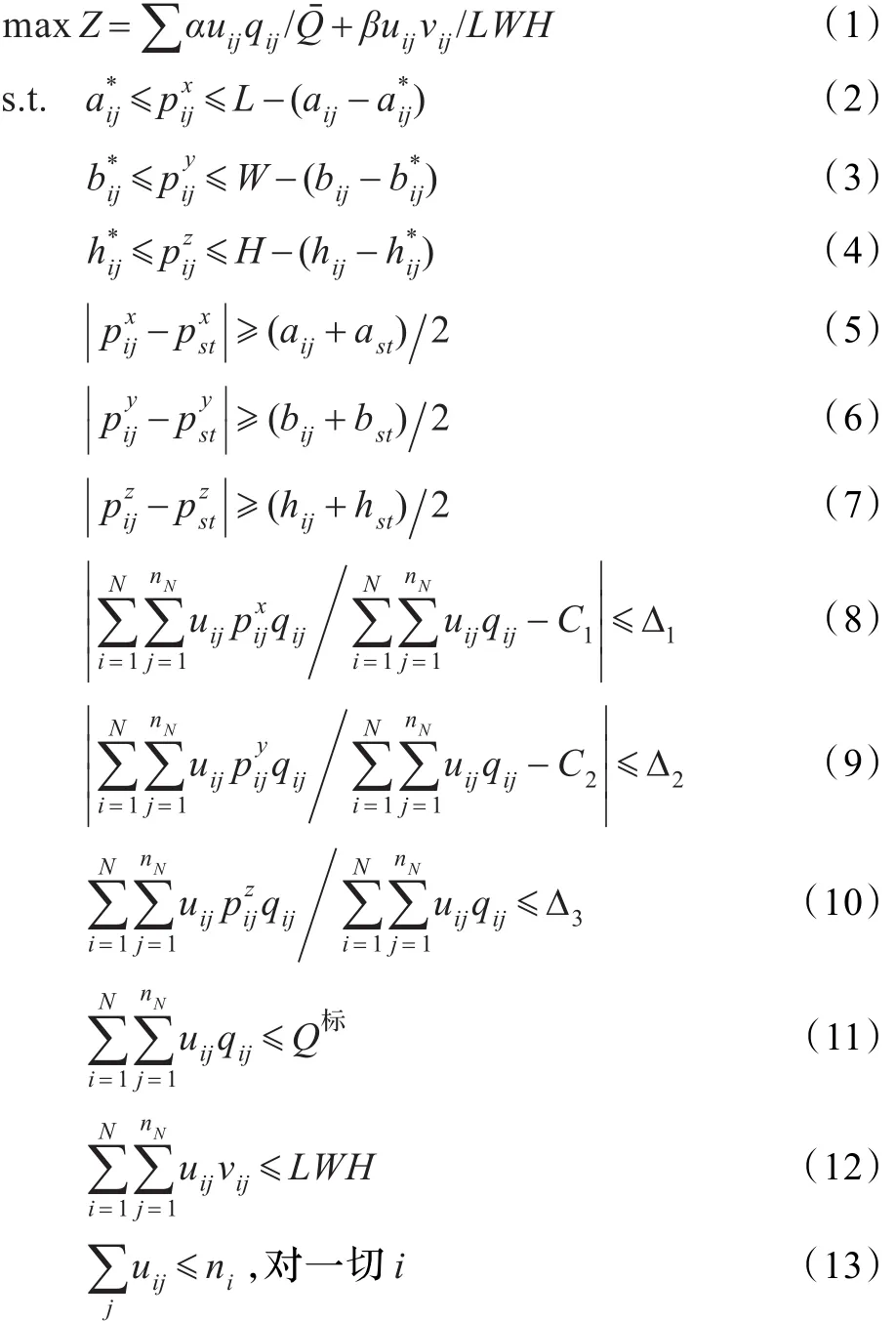
目标函数式（1）表示实现容积利用率与负载利用率综合目标最大化要求，权重系数α,β为常数，可根据装载对象性质等因素选取。约束条件式（2）、（3）和（4）分别表示装载的货物不超出箱子边界；式（5）、（6）、（7）表示装载货物之间互不干涉；式（8）、（9）、（10）为使用列车装运时对车厢重心在横向、纵向及高度方向的要求，其容许偏移量Δi(i=1,2,3)为已知量，可由承运工具参数和载重量确定，如铁路运输按《铁路装载加固规则》计算；式（11）、（12）为集装箱允许载重量和有效容积约束，式（13）为所装载货物总数量约束。

3 偏随机密钥遗传算法

针对上述模型，本文采取遗传算法与启发式构造法相结合的方法进行求解，即由遗传算法搜索出物品装载序列，再结合构造法实现物品的装入。通过遗传算法搜索装载序列的方法已获得相应的研究，但如何加快算法收敛并防止陷入局部最优一直是个难点。借鉴文献[13]提出的偏密钥随机遗传算法，本文将其应用于序列的优化。

偏密钥随机遗传算法基于0到1间的随机数字构建装载序列和实现遗传操作，由这些数字组成的向量可以表示问题的一个可行解，经过交叉操作新产生的向量仍将属于可行解。基于算法的动态特性，系统可以建立随机密钥向量与优化布局方案之间的有机联系。

3.1 个体编码

偏密钥随机遗传算法的初始染色体中前M个基因，可先按物品类型序号以升序排列，再根据以升序排列的随机密钥进行调整，可获得初始装载序列的物品部分编码（如图1所示）。物品摆放方向编码，可结合物品可放置方向规定以随机方式生成。

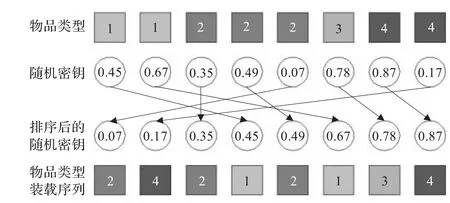
图1 物品装载序列基因编码

3.2 遗传操作

在算法中，对个体实行的遗传操作的过程包括复制、交叉及变异操作过程。复制过程采用精英策略，按一定比例从上一代复制优秀进入下一代。相比于概率复制方法，精英策略能有效地确保解的质量在进化过程不断获得提升。

与一般密钥随机遗传算法[14]交叉操作不同，偏密钥随机遗传算法交叉操作的两个个体，一个来自精英群体，另一个以随机方式从全部个体中产生，这样有助于加快收敛并提高解的质量[13]。如图2所示，染色体1代表精英个体，染色体2表示一般个体。设交叉概率为0.7，即子代以0.7的概率从精英父代中获得基因，以0.3的概率从一般个体中获得基因。以掷硬币的方式决定从哪个染色体选择基因，头面朝上时选择第一个染色体，否则选择第二个染色体。模拟抛掷一枚偏斜的硬币来产生随机数，该硬币有0.7的概率头面朝上。当生成的随机数小于等于0.7时，从第一个染色体获得基因；当随机数大于0.7时，选择第二个染色体产生基因。这样产生的子代更接近于精英个体，可起到加速收敛的作用。

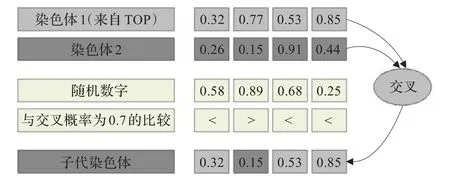
图2 交叉操作实例

一般的遗传算法以小概率在个体基因间进行的变异操作，而随机密钥遗传算法的变异操作在下一代种群中增加更多的新个体，即按照初始种群生成相同的分布，以随机方式来选择一些个体加入种群，从而起到防止早熟作用。全部遗传操作及新种群产生的过程如图3所示。

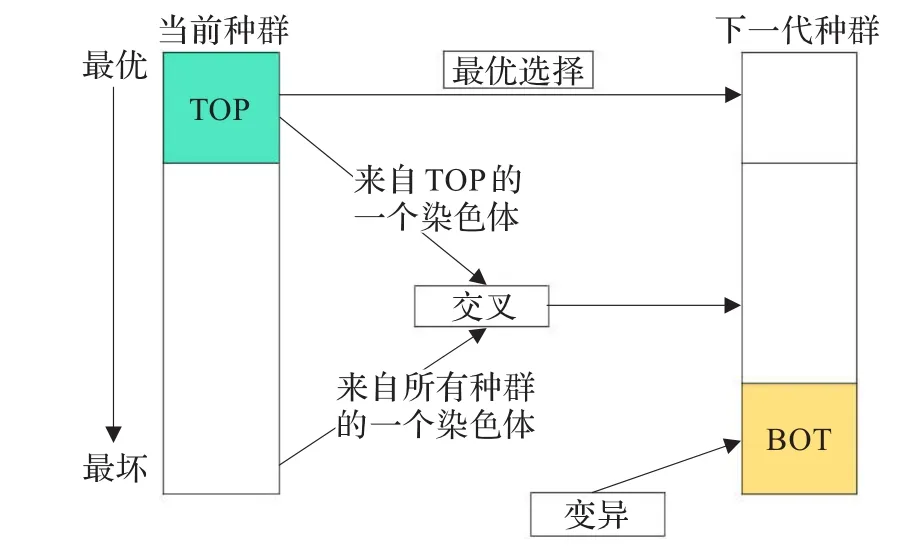
图3 新种群形成过程

4 基于极点的启发式装载法

4.1 极点装载法

对于搜索产生的物品装载序列ps，这里借鉴文献提出的极点法[15]（Extreme Points，EPs）并进行改进的基础上来完成装载，从而实现由装载序列向布局方案的转变。对于长、宽和高分别为lk、wk和hk物品k，选择某一装载模式并放置于箱中坐标为(xk,yk,zk)的左后下角位置时，将产生多个用于放置其他物品的新的极点，它们是由坐标值为(xk+lk,yk,zk)、(xk,yk+wk,zk)和(xk,yk,zk+hk)的点垂直投影到箱壁或邻近物品上而形成（如图4所示），这些点代表后续装载可以选择放置的位置。当箱子为空时，初始极点对应为箱子的两个对称角位置（可设左边为左后下角，右边为右前下角）；随着装载的进行，更多的极点随之形成，可作为后续装载可供选择的位置。

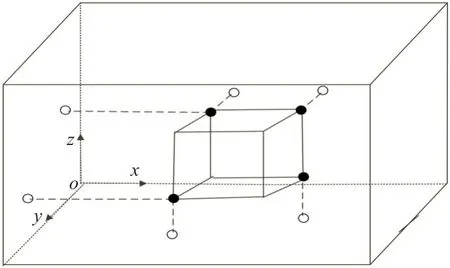
图4 极点产生过程

选择不同的极点放置物品将形成不同的装载模式，产生相应的装载效果，可按照一定的规则，从多个极点中选择一个作为当前物品的放置位置。不同于文献[15]使用极点的过程，为了加速平衡布局方案的形成，这里结合有助于重心平衡的启发式装载规则进行布局。借鉴左后下角（Left-Down-Back Conner）规则，采取同时从箱子左右两边以对称形式进行布局的方法，即左边从左后下角开始、右边从右前下角开始进行装载。从箱子两边同时展开装载有利于箱子四周形成相对紧凑的布局，空间碎片主要集中于中部位置，为借助中间位置物品位移实现整体重心调整创造了条件。

4.2 装载过程

为了实现上述对称装载的思想，借鉴文献[16]提出的锚距和锚角的方法来确定当前装载的极点。由于装载时货物一般放在空间的某个角落，将装载空间角与其对应的集装箱箱角间的距离称之为锚距，并使用曼哈顿距离衡量。锚距最小的角称为锚角，极点的选择以锚距最小为原则确定，即选择与箱子对称的两个角距离较近的极点位置放置货物。由此建立极点列表用以存储装载过程中新产生的极点，依据它们距离箱角的远近进行排序，并随装载的进行不断对极点序列进行更新。

货物装载是基于预先确定的货物序列，将货物依次放入极点序列指定的位置上。为了确保实施过程中各装载对象放置的稳定性，计算各物品底部支撑面积，要求确保其获得完全支撑。装载中若某一极点位置不能满足完全支持条件或无法装入当前物品时，则考虑极点列表中下一个极点，直至找到能满足装载条件的极点为止。若找不到适合的极点，则暂时放弃该物品装载，考虑装载序列中下一对象；而在后续的装载中，将优先考虑之前未装入的物品。每完成一次物品装入，按照排序规则对极点序列进行一次更新，同时记录剩余可用物品。以此方式持续下去，直至全部物品装入或箱子不能装入为止。基于极点的启发式装载方法的运行过程如图5所示。

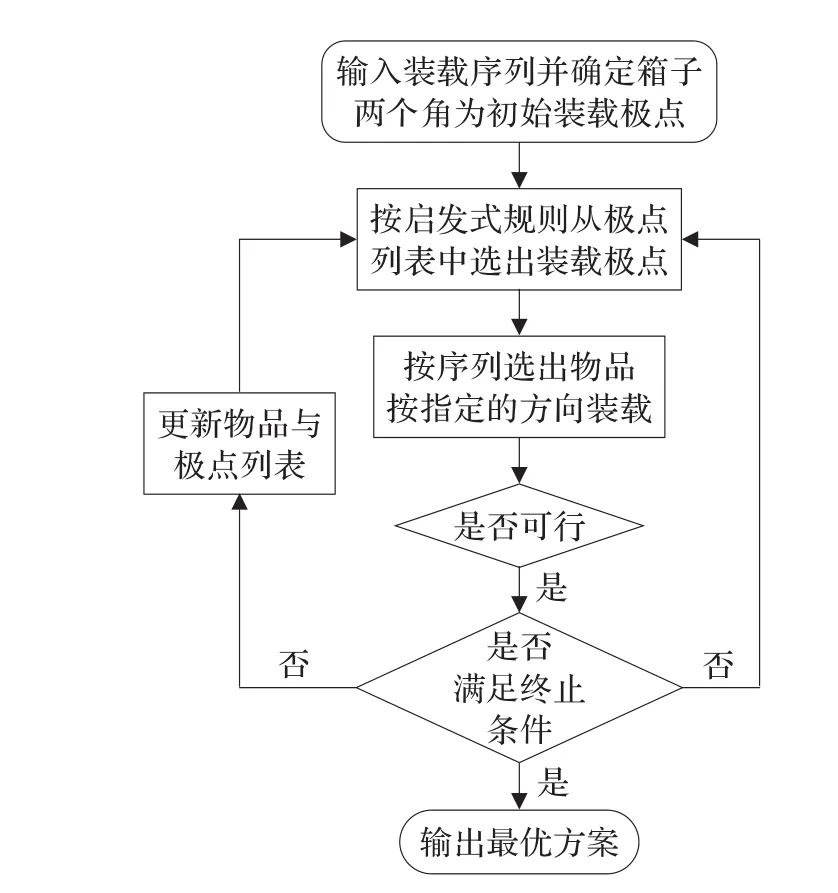
图5 启发式装载方法运行过程

4.3 重心优化

基于装载序列与启发式装载方法完成最优布置方案搜索后，可通过对确定的方案中部分物品实施位移，从而达到进一步装载重心的目的。物品的移动涉及移动的目标方向及可移动的范围等问题，需结合具体布局方案进行分析和确定，下面简要介绍物品移动的过程。

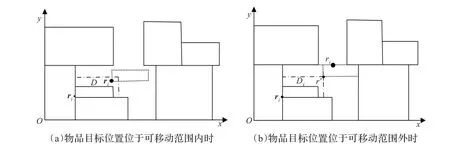
图6 物品移动示例

上述是基于理想的推导，实际操作过程中可能存在相互干涉而无法移动，因此需在确定移动对象后，对其可移动范围进行界定。如图6所示，设虚线框所围区域Di表示物品i的可移动范围，实心原点表示合重心理想位置。Di确定下来后，可按以下不同情形进行操作：

当Di={ϕ}为空集时，物品不移动；当∈Di时，移动物品i至r′以满足平衡条件（如图6（a））；当∉Di且Di≠{ϕ}时，可将i移至最接近于r′的中间位置r″，尽可能地接近于平衡（如图6（b））。另外，由于物品在三维空间的移动除了满足平衡条件外，还需考虑稳定性要求，因此物品在垂直方向的移动应确保其处于被支撑状态，可采取类似重力作用的情形作进一步移动，使其获得相应支撑。

5 实例

由于目前铁路集装箱两用车较少，常用敞车装运集装箱，本实例属这种情况。货物数据如表1，各件货物重心为其几何中心。车型为敞车C62，技术参数为：标记载重60 t，装载一个40英尺的集装箱，集装箱内部容积（1 199×233×235）cm3，允许载重量26.6 t，货物合重心最大允许横向偏移为10 cm，最大允许纵向偏移根据载重量计算。

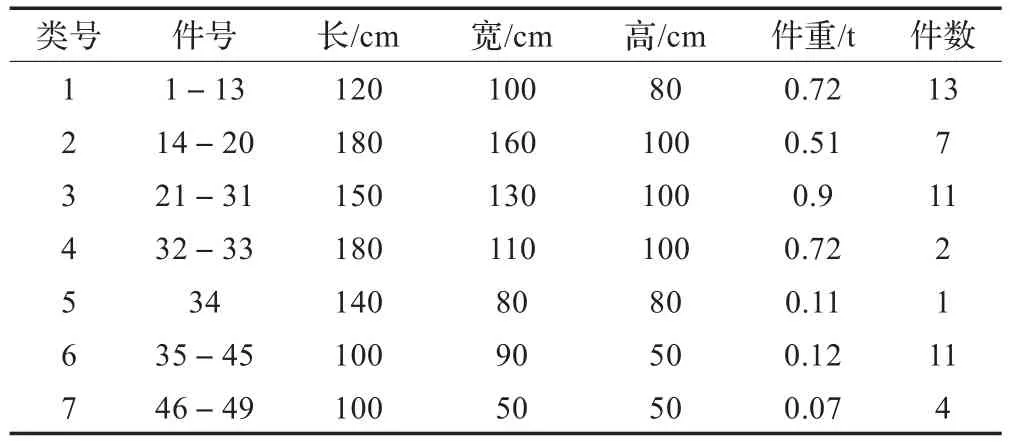
表1 货物数据表

根据上述模型及算法，运用C++语言进行编程。算法参数取值分别为：种群规模为30，交叉概率为0.7，精英个体复制比例为15%，随机生成变异个体比例为15%，终止条件为连续运行500代。使用Intel Core2 Duo2.0 GHz处理器运行程序，可制定货物的装载布局方案：布局示意图见图7；货物合重心的纵向、横向偏移量、重心高、车辆利用情况见表2；货物配装情况及布局位置见表3。

图7 装载方案布局示意图

表2 装载方案技术指标

从装载方案表中可以看出，待装货物中只有第2类和第5类各1件（编号20、34）未装入。货物合重心偏移及重车重心高度均在许可范围内，且偏移量较小，符合平衡装载要求；同时，集装箱的装载利用率都较好，尤其是有效容积利用率达到较高的水平。总体而言，获得的装载方案车辆利用效果好，且布局合理，满足各主要约束属于优良的布局方案。

6 结束语

针对考虑装载重心平衡等实践约束条件的铁路集装箱三维装箱问题，本文先使用偏随机密钥遗传算法进行物品装载序列的优化，然后基于各装载序列，采用基于极点的启发式方法进行装载模式的构建，再通过最优布置方案中部分物品位移，以实现布局重心优化的目的，几部分方法结合起来可获得最优装载方案。通过采集铁路装运现场的数据进行实验，验证了方法具有有效性。如何在装载模式构造过程中将重心调整结合起来考虑，以及根据货物类别特征等因素，确立装载算法选择机制等方面可作为下一步研究方向。

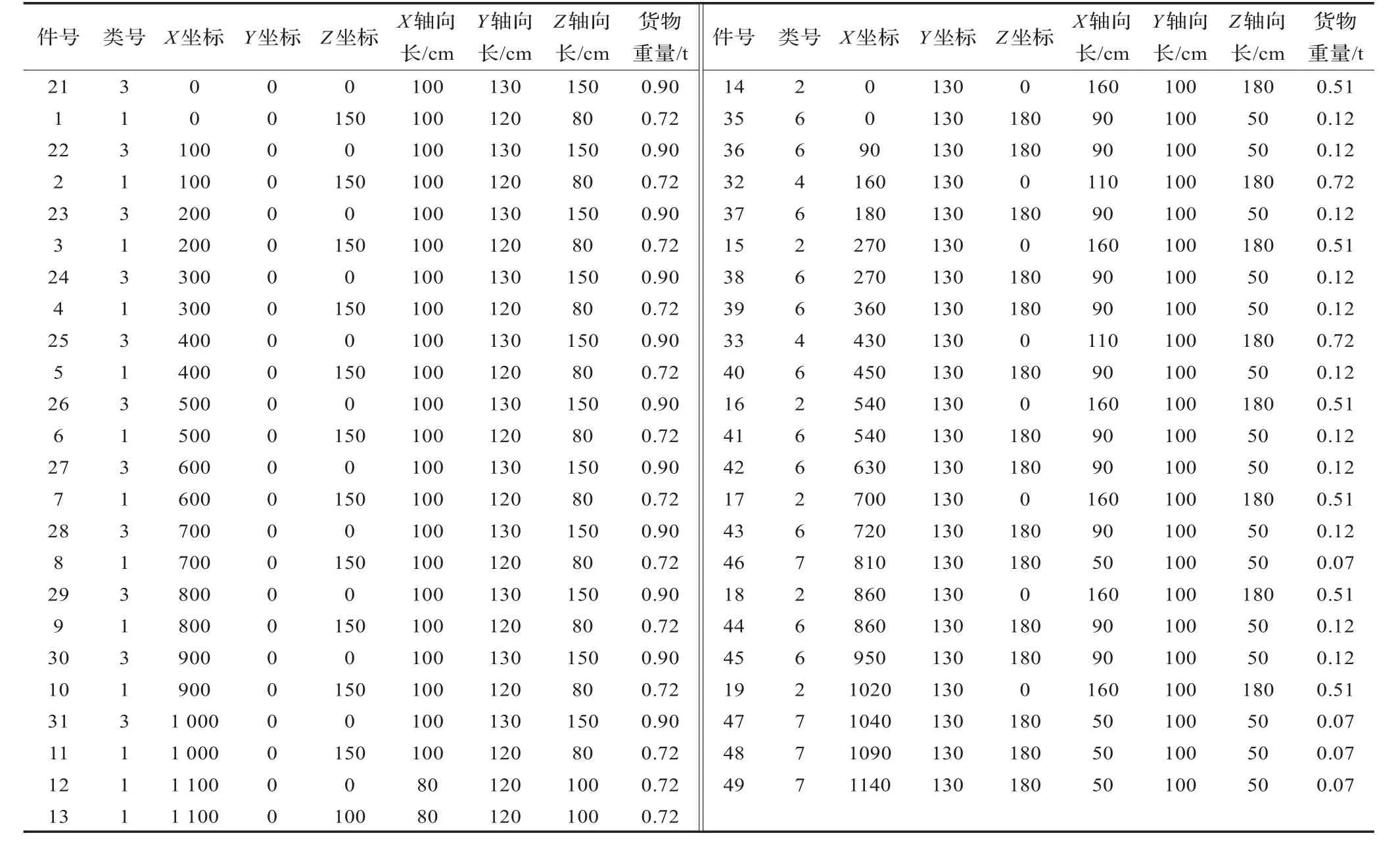
表3 货物配装情况及布局位置

[1]Pisinger D.Heuristics for the container loading problem[J]. EuropeanJournalofOperationalResearch，2002，141：143-153.

[2]Chen C S，Lee S M，Shen Q S.An analytical model for the container loading problem[J].European Journal of Operational Research 1995，80：68-76.

[3]Hifi M.Exact algorithms for the guillotine strip cutting/ packing problem[J].Computers Operations Research，1998，25（11）：925-940.

[4]Gehring H，Bortfeldt A.A genetic algorithm for solving the container loading problem[J].International Transactions on Operational Research，1997：401-418.

[5]Gehring H，Bortfeldt A.A parallel genetic algorithm for solvingthecontainerloadingproblem[J].International Transactions in Operational Research，2002，9：497-511.

[6]张德富，彭煜，朱文兴，等.求解三维装箱问题的混合模拟退火算法[J].计算机学报，2009，32（11）：2147-2156.

[7]Bortfeldt A.Gehring H，Mack D.A parallel tabu search algorithm for solving the container loading problem[J]. Parallel Computing，2003，29（5）：641-662.

[8]Liu J，Yue Y.A novel hybrid tabu search approach to container loading[J].Computers&Operations Research，2011，38：797-807.

[9]Moura A，Oliveira J F.A GRASP approach to the container-loading problem[J].IEEE Intelligent Systems，2005，20（4）：50-57.

[10]Davies A P，Bischoff E E.Weight distribution considerations in container loading[J].European Journal of Operational Research 1999，114（3）：509-527.

[11]Eley M.Solving container loading problems by block arrangement[J].European Journal of Operational Research，2002，141（2）：393-409.

[12]雷定猷.货物装运优化理论与应用研究[D].长沙：中南大学，2004.

[13]Gongalves J F，Resende M G C.Biased random-key genetic algorithms for combinatorial optimization[J].Journal of Heuristics，2010，17：487-525.

[14]Bean J C.Genetics and random keys for sequencing and optimization[J].ORSA Journal on Computing，1994，6：154-160.

[15]Crainic T，Perboli G.Extreme point-based heuristics for three-dimensionalbinpacking[J].InformsJournalon Computing，2008，20.

[16]Zhu W B，Lim A.A new iterative-doubling greedy-lookahead algorithm for the single container loading problem[J]. European Journal of Operational Research，2012，222：408-417.

[17]Zhu W B，Huang W L.A prototype column generation strategy for the multiple container loading problem[J]. European Journal of Operational Research，2011，223（2012）：27-39.

YOU Wei,LEI Dingyou,ZHU Xiang

School of Traffic&Transport Engineering,Central South University,Changsha 410075,China

The three-Dimensional Container Loading Problem（3DCLP）with practice constrains is a complex combinatorial optimization problem and has the typical characters of NP-hard.As to the tendency of convergence into local optimization of the basic Genetic Algorithm（GA）,the paper puts forward a method to optimize the loading sequence based on the biased random-key GA.Then the optimal layout to the boxes can be determined using a heuristic based on extreme-points approach.And the balance of the whole loading gravity center can be improved by the moving of parts of items lastly.The instance demonstrates that the algorithm can generate the optimizing packing plan quickly,in which the available capacity of the vehicle is utilized well and the requirements for the transportation safely are met.

three-Dimensional Container Loading Problem（3DCLP）;hybrid genetic algorithm;biased random-key;heuristic algorithm;balancing constraints

考虑实践约束的三维装箱问题属于复杂的组合优化问题，具有典型NP难问题的特点。针对一般遗传算法求解装箱问题易陷入局部最优的缺点，提出使用偏随机密钥遗传算法进行装载序列搜索，结合基于极点的启发式方法实现货物的优化布置，进而通过部分装载物品的位移来改善整体重心分布。经过实例运算和分析，证明提出的方法能快速制定货物优化布置方案，达到装载工具高效利用及货物安全运输的要求。

三维装箱；混合遗传算法；偏随机密钥；启发式算法；重心平衡

A

U294

10.3778/j.issn.1002-8331.1401-0284

YOU Wei,LEI Dingyou,ZHU Xiang.Biased random-key hybrid genetic algorithm for three-dimensional loading problem.Computer Engineering and Applications,2014,50（22）：265-270.

中国铁路总公司资助项目（No.2013X009-1）。

游伟（1961—），男，博士研究生，研究领域为交通运输；雷定猷，教授，研究领域为交通及物流；朱向，讲师，研究领域为物流工程。E-mail：1271446294@qq.com

2014-01-17

2014-06-05

1002-8331（2014）22-0265-06

CNKI网络优先出版：2014-07-02,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0284.html