变增益分段滑模控制的PMSM位置伺服系统研究

高锋阳，秦超，庄圣贤，董唯光

1.兰州交通大学自动化与电气工程学院，兰州 730070

2.沈阳铁路局科学技术研究所，沈阳 110013

3.西南交通大学电气工程学院，成都 610031

变增益分段滑模控制的PMSM位置伺服系统研究

高锋阳1，秦超2，庄圣贤3，董唯光1

1.兰州交通大学自动化与电气工程学院，兰州 730070

2.沈阳铁路局科学技术研究所，沈阳 110013

3.西南交通大学电气工程学院，成都 610031

1 引言

永磁同步电动机（Permanent Magnet Synchronous Motor，PMSM）优点多，应用广，是目前研究的热点电机之一[1]。滑模变结构控制对外界扰动、系统参数变化不敏感等优点，在永磁同步电机鲁棒性控制中具有重要意义。为解决传统PID控制位置伺服系统难以有效满足其高性能要求等问题，国内外学者已有将滑模变结构控制方法应用于永磁同步电机，并取得了一定的成果[2-3]。文献[4]将梯形速度波形设计成指数形式，并用两段滑模代替四段，优点是结构简单平滑稳定，但同时带来的不足就是快速性降低，并且存在抖振。文献[5]设计4个滑模面快速跟踪给定位置，但设计过于复杂，预估算信息繁琐，也降低了系统精度。文献[6]应用饱和函数代替开关函数，在一定范围内抖振得到抑制，但鲁棒性得到削弱。文献[7]通过|s|变化规律，将固定增益设计成变增益，抖振得到明显抑制，鲁棒性得到增强。文献[8]设计一种滑模控制器对控制量先微分后积分，使输出不含非线性项，减小抖振，不足是使系统变得复杂难于实现，且快速性降低。文献[9-10]将模糊控制、自适应控制与滑模控制相结合来抑制抖振，但定位过程中响应速度较慢。

为了提高永磁同步电机位置伺服系统的动静态品质。本文利用位置信号误差、滑模面积分与滑模增益的关系，构造出新型切换项变增益滑模控制器；并将单段滑模线控制扩展成PI与滑模分段控制；其中新型滑模控制器采用简化位置、速度控制器一体化的思想。通过仿真分析验证结果表明，该控制器提高了系统的鲁棒性，位置伺服系统的动静态性能得到增强，并且系统得以简化，易于工程实现。

2 永磁同步电机的数学模型

为了方便分析，简化PMSM数学模型[11]，首先对电机做如下假设：

（1）忽略铁心饱和、涡流和磁滞的影响，认为磁路线性，可用叠加原理分析。

（2）忽略电机绕组漏感，永磁材料的磁阻为零。

（3）转子上没有阻尼绕组，定子绕组三相对称。

（4）定转子绕组产生的气隙磁场正弦分布，忽略磁场的高次谐波。采用id=0的转子磁场定向控制。电压方程[12]如下：

3 控制器的设计

3.1 传统滑模变结构控制器的设计

滑模变结构控制是对非线性不确定系统的一种有效的综合控制方法，其基本思想是设计一预设滑模面，保证从任意一点出发的状态轨迹通过控制器的作用引导到预设的滑模面，并保证系统在滑模面上的运动是渐近稳定的。本文采用的等效控制方法是由等效控制部分Ueq和切换控制部分kfsgns组成。Ueq是滑模运动的控制量，对于标称系统F=0，滑模面的运动满足ds/dt=0，由此可得Ueq值。实际系统控制中，为保证系统在扰动情况下仍保持趋向滑模面及稳定点，故引入kfsgns。等效控制方程[13]为：

为了使系统无超调地到达稳定，选择一阶滑模面[14]：

3.2 改进的滑模变结构控制器设计

传统等效控制方法中kf的大小影响系统鲁棒性能和滑模抖振强度。kf值越大系统鲁棒性能越好，但同时抖振的增大会影响控制器的性能。本文设计一种新型控制器，即：

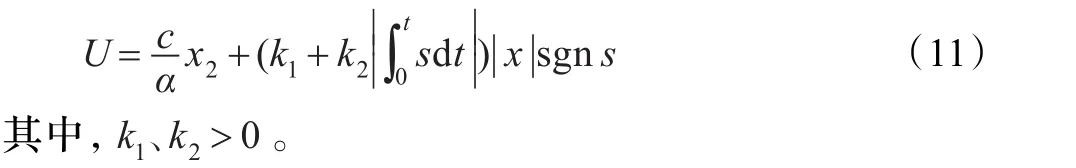
传统的切换项增益的选取为固定值，不能满足系统不同运动阶段的动态要求。本文中对增益做出改进，其中，当s初始值较大时，滑模增益在满足系统鲁棒性要求的同时会带来不必要的过大滑模抖振，因此，在改进中引入变量k2进行调节；当s趋近于0时，s的积分项趋近于一个较小常数，过小的滑模增益同样对系统带来不稳定等不利的影响，所以引入变量k1进行补偿；此外，引入位置误差变量|x|对系统进行自动调节，保证系统运动过程中在无限接近稳定点时，位置误差不断减小，并最终实现到达稳定点时，保证滑模切换项增益为0，进一步达到削弱抖振的目的[15]。

结合方程（10）、（11）可得最终控制量U：

式中，σ为一个数值较小的正常数。

3.3 稳定性分析

滑模存在和稳定的基本条件，可利用Lyapunov稳定性理论[16]进行分析，取Lyapunov函数为：

由于SMC的可达性条件为ss˙＜0，所以保证V˙(x)＜0，即能保证系统进入滑动模态。由方程（7）、（8）可得：

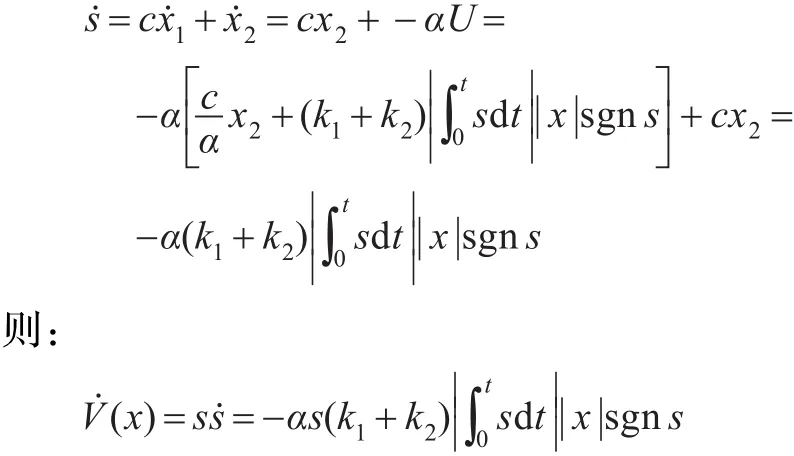
其中k1、k2＞0，s·sgn(s)≥0，α＞0，所以s＜0。即进入滑模面后系统进入滑模运动，系统是稳定的。

3.4 滑模变结构控制与PI分段控制

根据定位时间最优原则，通常将速度曲线设计成梯形，一般分四个阶段：加速段、恒速段、减速段和位置接近段，如图1所示。

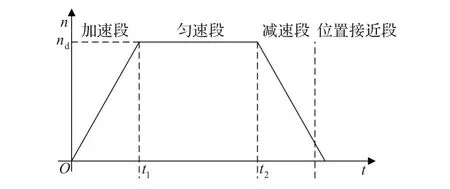
图1 电机伺服系统的梯形速度曲线

为获得良好的梯形跟踪速度曲线，国内外学者提出以下两种主要解决方法：（1）根据系统运行的加速度、减速度、匀速段和位置接近段四个阶段分别设计四个滑模面。这种方法位置、加速度等信息需要预估算，且滑模面多，系统比较复杂，较难实现。（2）加速和减速阶段采用结构不变的控制方式，以限定的最大加速、减速进行启动运行。在恒速段和位置接近段采用滑模控制，提高系统鲁棒性和定位精度。这种方法虽然系统得到简化，但在给定位置较小时，切换点速度过大，会引起较大电流冲击，且这样设计没有减少实际切换量。

针对以上问题，本文采用滑模变结构控制与PI控制分段控制的组合控制器。其中加速段采用不变的PI控制方法，以限定的最大加速进行启动运行；恒速段、减速段和位置接近段应用滑模变结构控制的强鲁棒性及优良的动静态性能设计成单段滑模进行控制；应用Simulink设计出PI与SMC切换开关模块。采用两段控制代替之前的四段控制方法，既能完全满足系统位置伺服快速跟踪给定的设计要求，又简化滑模面设计，减少切换次数，提高了系统鲁棒性的同时，对抖振进行抑制。

4 仿真分析

为了验证新型分段控制器的性能，建立Simulink系统仿真模型，电机参数如下：Rs=2.875 Ω；Ld=Lq= 0.008 5 H；ψa=0.175 Wb；J=0.008 kg·m2；极对数p=4。系统仿真框图如图2所示，其中滑模变结构与PI分段控制器模块如图3所示。

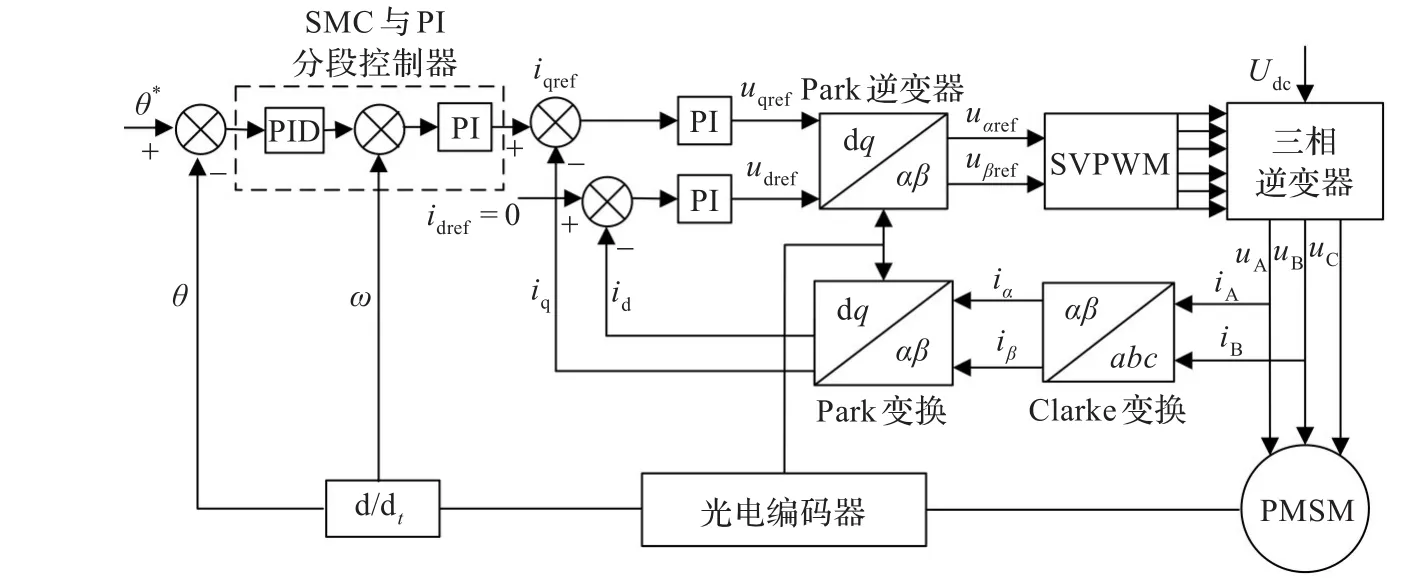
图2 永磁同步电机伺服控制系统框图

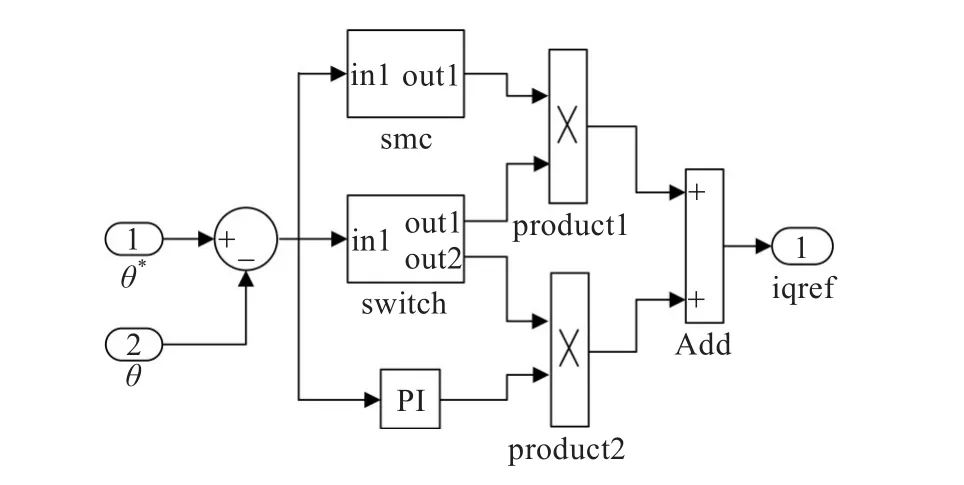
图3 滑模控制与PI分段控制器

图4为系统给定大位置50π时速度波形仿真结果。可见图4（a）中PI控制下，系统启动存在较大超调，且转速恢复到稳定调整时间较长。速度稳定运行阶段波形存在少量波动。位置接近段速度调整到零点的时间较长，位置到达给定值后，转速波形平滑稳定；图4（b）中传统滑模变结构控制器作用下，系统启动迅速，超调量较PI控制条件下有所减小，恢复转速稳定过程较快。稳定运行阶段速度波形较稳定，对波动有了很好的抑制。转速过渡到零点调整时间较PI控制明显缩短，不足的是在位置到达给定值后，系统存在的滑模固有抖振明显。图4（c）中改进的分段滑模控制较传统未分段SMC、PI控制启动更快，超调更小，调整到达转速稳定时间更短，转速稳定运行更为平滑。位置接近段过渡到达零点的转速调整时间较传统未分段滑模进一步缩短。与图4（b）对比可以清楚得出，在到达给定位置后，改进型分段滑模控制的系统转速相比未分段传统滑模控制器的固有抖振有了明显抑制。

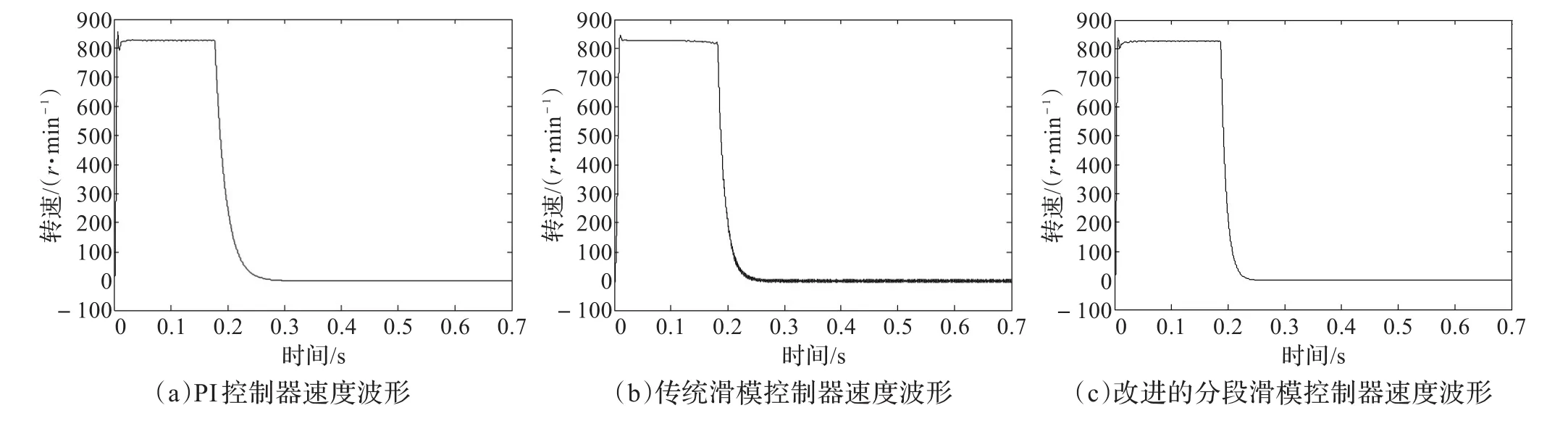
图4 系统给定大位置速度波形

图5为系统给定大位置50π时转矩响应波形。图5（a）中传统SMC控制转矩波形抖振较大；图5（b）中为改进的分段滑模变结构控制器转矩波形，可以看到，在0.01 s时刻，转矩达到最大值，为电机快速启动提供最大助力，此后转矩开始调整，在0.015 s时与传统未分段滑模波形图比较可得，改进型滑模分段控制转矩值更小，即能保证系统制动能力更强，且更快速地到达稳定。在0.02 s时波形恢复到稳定负载转矩值，此过程为超调量调整阶段。系统运行到0.18 s时，转矩突降到最小值为位置接近段提供制动，保证系统快速无超调地跟踪给定位置值。经过0.05 s的调整，转矩再次恢复到稳定值，并保持该状态持续运行。通过图5（a）和图5（b）波形对比可得在转速稳定段、位置接近段改进的分段滑模控制方法对滑模固有抖振抑制明显，并且电机启动和系统调整时间的快速性等方面较传统未分段滑模有所提高。

图7（a）为改进的分段滑模变结构控制系统给定大位置50π并在0.1 s时突增负载的速度波形仿真结果，由图可以看到，转速在0.1 s时发生变化，快速下降，并在0.15 s无超调平滑的到达新的稳定。可见稳定后转速波形仍对系统波动和滑模抖振有很好的抑制作用，并在0.25 s时第二次快速平滑的到达新的稳定状态。通过图7（b）与图6即改进型滑模分段控制突增负载与恒负载运行的位置仿真波形对比可得，在0.1 s突增负载时改进型分段滑模控制下的位置波形无较大波动，且波形实现平滑过渡。通过以上仿真结果可以充分验证改进型滑模分段控制下的系统在外界扰动的情况下，仍能保持良好性能，且具有较强鲁棒性。

图8为改进型分段滑模控制器小位置4.5π给定的速度波形，可以看到转速在0.02 s时有小幅波动，这是因为位置即将到达额定值，为了使电机没有太大超调而必须使转矩施加反力，对电动机产生制动的效果，这样有利于使位置精确定位。由小位置给定仿真图可得，改进型分段滑模控制系统性能稳定，在给定不同初始条件时，系统仍能保持良好性能。

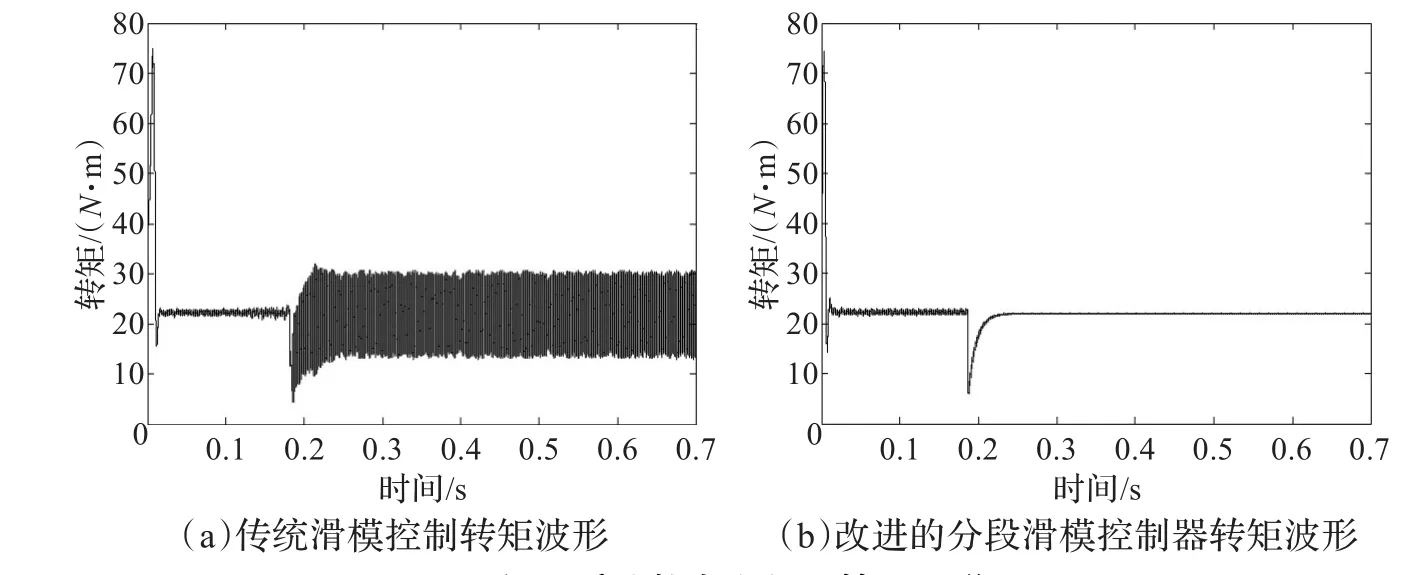
图5 系统给定大位置转矩波形

图6 改进SMC给定大位置位置波形

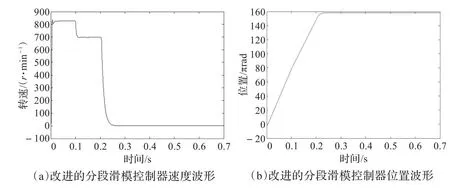
图7 系统给定大位置突增负载响应波形

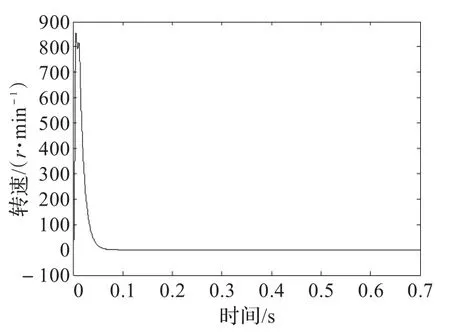
图8 系统给定小位置时改进的分段滑模控制器速度波形

5 结束语

针对滑模变结构控制应用于永磁同步电机位置伺服系统中出现的问题，提出一种新颖的变参数滑模变结构等效控制方法；将传统的4段滑模控制简化为PI与滑模分阶段作用的两段控制，并自主设计出切换开关模块。该设计方法很好地解决了滑模切换面过多，电流冲击大等问题，其主要优点有：

（1）减少滑模面、切换量数目，对系统进行简化，易于实际应用。

（2）对滑模固有抖振抑制明显，提高了位置伺服系统精度。

（3）系统鲁棒性及动静态性能突出，速度波形启动时超调量小，调整时间少；减速段到位置接近段快速性明显增强。

在永磁同步电机位置伺服系统中，提出将改进的变增益滑模等效控制方法与传统PI控制相结合组成分段控制器。仿真结果表明新型分段滑模控制器鲁棒性优于PI调节器和传统未分段滑模调节器，对滑模固有抖振抑制明显，并使系统能快速跟踪给定位置。该方法使永磁同步电机位置伺服系统性能得到提升。

[1]Kuo-Kai，Lai Chiu-Keng，Tsai Yao-Wen.A newly robust controller design for the position control of permanent magnet synchronousmotor[J].IEEETransactionsonIndustrial Electronics，2002，49（3）：558-565.

[2]陈荣.永磁同步电机控制系统[M].北京：中国水利水电出版社，2010：1-27.

[3]陈志梅，王贞艳，张井岗.滑模变结构控制理论及应用[M].北京：电子工业出版社，2012：1-13.

[4]胡强晖，胡勤丰.全局滑模控制在永磁同步电机位置伺服中的应用[J].中国电机工程学报，2011，31（18）：61-66.

[5]Lai C，Shyu K.A novel motor drive design for incremental motion system via sliding-mode control method[J].IEEE Transactions on Industrial Electronics，2005，52（2）：499-507.

[6]Zhang D Q，Panda S K.Chattering-free and fast response sliding mode controller[J].IEEE Pro-Control Theory，1999，146（2）：171-177.

[7]Wu S T，Shao Y J.Adaptive vibration control using a virtualvibration-absorbercontroller[J].JournalofSoundand Vibration，2007，305（45）：891-903.

[8]黄佳佳，周波，李丹，等.滑模控制永磁同步电机位置伺服系统抖振[J].电工技术学报，2009，24（11）：41-47.

[9]马义方，蔡际令，王雄海.伺服系统的自适应模糊滑模最优控制研究[J].浙江大学学报，2006，40（6）：1032-1035.

[10]Lin F J，Chiu S L.Adaptive fuzzy sliding mode control for PM synchronous servo motor drives[C]//IEEE Proc-Control Theory Apply，1998，145（1）：63-72.

[11]Kim M，Song D.A robust control of permanent magnet synchronous motor using load Torque estimation[C]//IEEE Int Symposium on Industrial Electronics Pusan，Korea，2001.

[12]谭文，王耀南，黄创霞，等.永磁同步电机中混沌现象的滑模变结构控制[J].计算机工程与应用，2009，45（11）：220-222.

[13]刘恒.永磁同步电机混沌系统光滑二阶滑模控制[J].计算机工程与应用，2012，48（21）：222-224.

[14]刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005：4-51.

[15]童克文，张兴.基于新型趋近律的永磁同步电机滑模变结构控制[J].中国电机工程学报，2008，28（21）：102-106.

[16]王丰尧.滑模变结构控制[M].北京：机械工业出版社，1998：31-50.

GAO Fengyang1,QIN Chao2,ZHUANG Shengxian3,DONG Weiguang1

1.School of Automation and Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China
2.Science and Technology Research Institute of Shenyang Railway Administration,Shenyang 110013,China
3.School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China

The sliding gain choice directly influence the robustness of the sliding mode control result of chattering.By using position signal error,sliding mode surface integral and sliding gain the non-linear relationship among this novel,present the design method of sliding gain.Combining the position control is a novel design method of the equivalent control method to improve the robustness of sliding mode control,weaken the sliding mode variable structure of chattering.In addition, the sliding line is extended to a control method of PI and sliding mode control effect in different stages in PMSM’s servo system.The application of Matlab/Simulink established permanent magnet synchronous motor servo system simulation model.The simulation results show that this scheme is with strong robustness,good static,dynamic characteristics and significantly decreasing buffeting.

position servo;sliding mode control;permanent magnet synchronous motor;vector control;chattering

滑模增益的选择直接影响系统抖振，利用位置信号误差、滑模面积分与滑模增益之间的非线性关系来设计滑模增益，再结合等效控制方法来削弱滑模抖振改善系统的鲁棒性。将单段滑模线控制扩展成在不同阶段PI与滑模分别起作用的两段控制方法应用于永磁同步电机位置控制。应用Matlab/Simulink建立了永磁同步电动机伺服系统的仿真模型，仿真结果表明该方案对系统参数不确定、外界扰动具有强鲁棒性。系统动静态品质优良，滑模控制的抖振得到明显抑制。

位置伺服；滑模变结构控制；永磁同步电机；矢量控制；抖振

A

TM351

10.3778/j.issn.1002-8331.1402-0300

GAO Fengyang,QIN Chao,ZHUANG Shengxian,et al.Sliding mode variable structure control of PMSM based on novel exponential rate reaching law.Computer Engineering and Applications,2014,50（22）：238-242.

甘肃省科技支撑计划资助项目（No.1204GKCA038）。

高锋阳（1971—），男，教授，硕士研究生导师，主要研究领域为大功率电源及交流调速技术；秦超（1988—），男，硕士研究生，主要研究领域为电力电子与电力传动；庄圣贤（1964—），男，教授，博士研究生导师，主要研究领域为交流技术及传动控制；董唯光（1971—），男，副教授，硕士研究生导师，主要研究领域为非线性系统控制。E-mail：18298379518qinshihuang1988@126.com

2014-02-25

2014-05-19

1002-8331（2014）22-0238-05

CNKI网络优先出版：2014-06-18,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0300.html