时延相关网络控制系统的输出反馈镇定

张雪峰,沈艳霞,童向荣

(1.江南大学理学院,江苏 无锡 214122;2.江南大学物联网工程学院,江苏 无锡 214122;3.烟台大学计算机学院,山东 烟台 264005)

网络控制系统(networked control system,NCS)是采用通信网络将分布的控制器、传感器、执行器连接的闭环控制系统．网络控制系统具有易于部署、维护和可实现远端控制等特点,所以相关领域的应用得到了迅速发展．同时,因为通信网络的引入,出现了一些新的问题,比如数据丢包、网络诱导时延、错序等,造成了系统不稳定或性能下降．目前,NCS已经成为学者的研究热点[1-3]．

时延现象在通信网络中是不可避免的问题．时延可能是常值的、时变的、随机的,给系统分析和设计带来很大的难度,从而获得了广泛的关注,也得到了一些重要成果．文献[4]采用混合系统方法分析了具有常值网络时延的NCS稳定性和控制器设计问题．文献[5]对存在输入延迟和测量输出延迟情形的NCS进行了研究,基于一个Lyapunov泛函,提出了输出反馈镇定控制器存在的充分条件．网络时延常具有一定程度的随机表现,所以随机建模成为此类问题研究的重要方法．Seiler研究了具有随机丢包的网络系统控制模型,基于Markov跳变参数的离散线性系统来进行设计H∞最优控制器[6]．文献[7]采用满足Bernoulli分布的二进制序列来描述数据传输的随机时延,利用矩阵不等式方法给出了动态输出反馈控制器存在的充分条件．

在实际情形中,因为通信网络结构的复杂性和网络应用的不确定性,造成通信网络时延不总是固定的,时延随机统计信息有时也难以确切得到;对于时变时延情形,有些文献忽略了时延动力学信息的考量,等等,得到的有关结论还具有一定的保守性．

对于NCS时延是时变的,并且时延随机动力学信息不可确知情形,本文采用E.Fridman提出的广义方法[8],并考虑了时延动力学信息,选用了时延相关切换控制器,得到了系统逐渐稳定的LMI充分条件,所得结果具有较小保守性．

1 问题描述

考虑图1所示的网络控制系统．假设传感器的数据采用单包传输,网络时延发生在传感器和控制器之间,传感器工作方式是时间驱动的,控制器和执行器工作方式是事件驱动的．

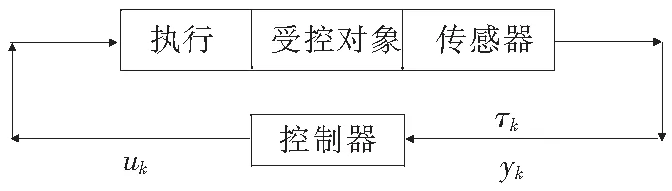
图1 NCS结构示意图

考虑被控对象系统为如下离散系统

xk+1=Axk+Buk,

(1)

其中:k∈Z,xk∈Rn是系统状态,uk∈Rp是系统的控制输入．

量测方程为

yk=Cxk-d(k),0

(2)

其中:yk∈Rm是经过网络时延到达控制器的量测输出,τk=d(k)是网络时变时延,d(k)∈S={d1,…,d2},S∈N+,d1,d2分别时延的最小值和最大值．

在NCS中,假设系统输出可测．因为控制器端可以通过数据包时问戳获得传感器到控制器的网络时延,所以采用如下依赖于传感器到执行器网络时延的输出反馈切换控制器

(3)

引理1[9]:给定适当维数的矩阵X,Y,Z,和Y>0,则有

-XTZ-ZTX≤XTYX+ZTY-1Z.

2 控制器设计

由式(1)、(2)和(3)构成的闭环系统为

(4)

其中:

φ(s),s=-d2,-d2+1,…,-1,0是初始条件．

定理1 对于给定的控制器(3),系统(4)渐近稳定的充分条件是:对于每个模态rk=i,i∈S,存在矩阵X>0,Z>0,U>0,Ni1,Ni2,Ni3,Si1,Si2,Si3,使得下列矩阵不等式成立:

(5)

其中:

证明系统(4)可写为如下等价广义形式

构造李亚普诺夫函数为

(7)

其中:X>0,Z>0,U>0．令k时刻和k+1时刻的模态分别为i和j,即rk=i,rk+1=j,i,j∈S.于是可得到：

ΔV1(k)=V1(k+1)-V1(k)=

(8)

ΔV2(k)=V2(k+1)-V2(k)=

ΔV3(k)=V3(k+1)-V3(k)=

(9)

令l=k+θ-1,由式(9)可得

可得

ΔV4(k)=V4(k+1)-V4(k)=

令l=k+θ,可得

(11)

由式(8)到(11)可得

ΔV(k)=V(k+1)-V(k)≤

(12)

(13)

根据式(6)中的第2式,对任意适当维数的矩阵Si1,Si2,Si3,下列等式对每个rk=i成立

(14)

由引理1,下列不等式成立

(15)

其中:

(16)

将式(13)、(14)加到(12),结合(15)得到

(17)

其中:

利用Schur补偿方法,Φi<0等价于Λi+d2Qi<0,从而系统(4)是渐近稳定的．证毕．

若控制器(3)中系数矩阵未知,则式(5)不是LMI,不能直接求解．若想求得控制器系数矩阵,必须将式(5)转化为LMI.为此下面给出求解式(5)并获得控制器的方法．

令Si1=αi1εiI,Si2=αi2εiI,Si3=αi3εiI,则得到定理2.

(18)

则存在控制器(3)使得闭环系统(4)渐近稳定．控制器系数阵为

其中:

3 数值算例

考虑网络控制系统被控对象的状态方程为

时延d(k)在1和2之间切换．令a11=1,a12=0.02,a13=1,a21=2,a22=0.02,a23=2．解不等式(18)可得如下可行结果

Ac(1)=0.268 2,Bc(1)=-0.013 3,Cc(1)=-0.030 3,Dc(1)=-0.096 4,

Ac(2)=0.258 9,Bc(2)=-0.001 2,Cc(2)=-0.289 2,Dc(2)=-0.035 1．

所以该闭环系统是渐近稳定的．

图2给出时延在1和2间切换时闭环系统的仿真结果,图3为时延切换状态．从图2可看出该闭环系统是渐近稳定的．

图2 闭环系统的状态轨线

图3 时延τk

4 结 论

在NCS中,对于传感器向控制器传输数据出现时变网络时延情形,采用切换控制器和广义系统方法,利用LMI解决了输出反馈镇定问题．本方法考虑了时延动力学信息,具有较少的保守性．本文提出的方法可为研究网络控制系统中出现的数据丢包、带宽约束等问题提供参考．

参考文献:

[1]Yu Mei, Xie Guangming, Wang Long. Stabilization of networked control systems with transmission delays[C]//Proceedings of the IEEE International Conference on Systems, Man and Cybernetics.Piscataway: USA IEEE, 2004:1764-1769.

[2]朱菲, 李玉清. 大时延NCS的研究现状及前景分析[J]. 通信技术 ，2007，40(11):273-274.

[3]Ma Weiguo, Shao Cheng. RobustH∞control for networked control systems[J].Journal of Systems Engineering and Electronics.2008,19(5):1003-1009.

[4]张湘,肖建. 网络控制系统的输出反馈控制[J].华中科技大学学报,2008,36(10):32-36.

[5]Zhang Wei, Branicky M S,Phillips S M.Stability of networked control systems[J].IEEE Control System Magazine,2001,21(1):84-99.

[6]Seiler Pete, Sengupta Raja.AnH∞approach to networked control[J].IEEE Trans on Automatic Control,2005,50(3):356-364.

[7]王武,林琼斌,蔡逢煌,等. 随机时延网络控制系统的H∞输出反馈控制器设计[J].控制理论与应用,2008,25(5):920-924.

[8]Fridman E. New Lyapunov-Krasovskii functionals for stability of linear retarded and neutral type systems [J]. Systems & Control Letters, 2001,43(4): 309-319.

[9]Xie Lihua, de Souza, Carlos E. RobustH∞control for linear systems with norm-bounded time-varying uncertainty[J].IEEE Transactions on Automatic Control,1992,37(8):1188-1191.