求解随机微分方程split-step欧拉方法的收敛性

贾俊梅

(内蒙古工业大学理学院,内蒙古 呼和浩特 010051)

随机微分方程在描述现象中起着越来越重要的作用,其理论广泛应用于金融、生物、物理、微电子、机械等学科和工程领域.但是除了少数随机微分方程,一般的随机微分方程很难求其理论解,因而数值方法的构造显得尤为重要. 多数情况下是将随机微分方程离散化为差分方程,然后利用随机差分进行计算或模拟.在所有的离散化方法中,欧拉格式是最基本且最重要的一种[1-13]. 在文献[1]中Wang和Li给出了自治标量split-step欧拉方法的数值格式,并且求其收敛性和稳定性,本文将文献[1]中提出的split-step欧拉方法推广到求解一般的伊藤型随机微分方程,并且求其收敛性.

1 split-step欧拉方法

考虑一维伊藤型随机微分方程(SDE)

dx(t)=f(x(t),t)dt+g(x(t),t)dw(t),t∈[0,T],x(0)=x0.

(1)

式中:f,g为R×[0,T]上的连续可测函数,分别称为偏移系数和扩散系数;w(t)是标准的Wiener过程, 其增量Δw(t)=w(t+h)-w(t)服从正态分布N(0,h).00,K2>0,使得

|f(x,t)-f(y,t)|2∨|g(x,t)-g(y,t)|2≤K1|x-y|2.

(2)

|f(x,t)|2∨|g(x,t)|2≤K2(1+|x|2) .

(3)

方程(2)、(3)保证方程(1)解的存在并且唯一. 对于方程(1) split-step欧拉方法,即扩散项split-step欧拉(DISSE)方法:

(4)

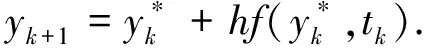
(5)

和偏移项split-step欧拉(DRSSE)方法:

(6)

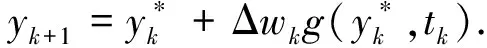
(7)

当t∈[tk,tk+1)时,定义

(8)

(9)

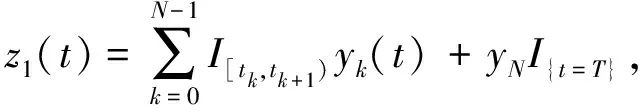
(10)

(11)

由方程(10)、(11)方程(8)可以写成如下的形式

(12)

由方程(10)、(11)方程(9)可以写成如下的形式

(13)

2 split-step欧拉方法的均方收敛性

在这部分,来证明split-step欧拉方法的均方收敛性.主要证明扩散项split-step欧拉(DISSE)方法的均方收敛性,偏移项split-step欧拉(DRSSE)方法的均方收敛性的证明过程类似.此证明类似于文献[2].为了证明主要的定理,将使用如下几个引理.

引理1 设h<1并且方程(3)成立,那么存在2个正常数A=1+K2,B=K2,使得

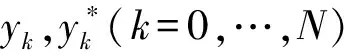
对以上方程两边求数学期望并由h<1,得到

(14)

引理2 设h<1并且方程(3)成立,那么存在2个正常数F,G,使得

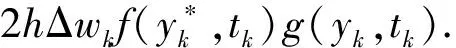
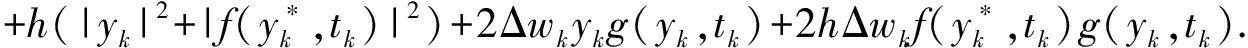
对上式两边求数学期望,由h<1和引理1,得.

E|yk+1|2≤E|yk|2+(1+K2+2AK2)hE|yk|2+(3K2+2k2B)h=(1+Ch)E|yk|2+Dh,

其中:C=(1+K2+2AK2),D=(3K2+2K2B).由Gronwall不等式得

引理3 在引理2成立的条件下,那么存在一个正常数H(H不依赖h)使得

E|y(t)-z1(t)|2∨E|y(t)-z2(t)|2≤Hh.

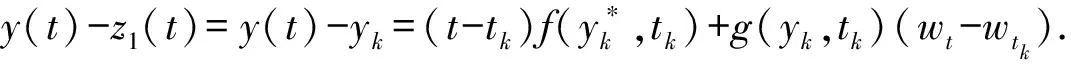
所以 |y(t)-z2(t)|2≤K2h(10+6F+4G).

E|y(t)-z1(t)|2∨E|y(t)-z2(t)|2≤Hh,这里H=K2(10+6F+4G).

定理设x(t)是方程(1)的解析解,f、g满足方程(2)、(3)且h≤1.假设存在一个正常数K3使得

|f(x,s)-f(x,t)|2∨|g(x,s)-g(x,t)|2≤K3(1+|x|2)|s-t|

(15)

证明由方程(1)、(12), 当t∈[0,T]

由Höder不等式,

由方程(2)、(16)和基本不等式(a+b)2≤2a2+2b2,

由殃矩不等式,

由引理1、2、3得

Th(K1H(8T+32)+K3(4T+4TG+16F+16)).

其中:M=T(K1H(8T+32)+K3(4T+4TG+16F+16))e(8T+32)K1T.

证毕.

DRSSE方法的均方收敛性的证明与DISSE方法的类似,所以在这里省略.

参考文献:

[1]Wang Peng, Li Yong. Split-step forward methods for stochastic differential equations [J]. Journal of Computational and Applied Mathematics, 2010, 233: 2641-2651.

[2]Ding Xiaohua, Ma Qiang, Zhang Lei. Convergence and stability of the split-stepθ-method for stochastic differential equations[J].Computers and Mathematics with Applications, 2010, 60: 1310-1321.

[3]Fan Zhengcheng,Liu Mingzhu,Cao Wanrong. Existence and uniqueness of the solutions and convergence of semi-implicit Euler methods for stochastic pantograph equation[J]. J math Anal Appl, 2007, 325: 1142-1159.

[4]Marion G,Mao Xuerong, Renshaw E. Convergence of the Euler shceme for a class of stochastic differential equations[J]. International Mathematical Journal, 2002, 1(1):1-14.

[5]Zhang Haomin, Gan Siqing, Hu Lin. The split-step backward Euler method for linear stochastic delay differential equations[J]. Journal of Computational and Applied Mathematics, 2009, 225: 558-568.

[6]Cao Wanrong.T-stability of the semi-implicit Euler method for delay differential equations with multiplicative noise[J]. Applied Mathematics and Computation, 2010,216: 999-1006.

[7]Zhang Xicheng. Euler-Maruyama approximations for SDEs with non-Lipschitz coefficients and applications[J]. J Math Anal Appl, 2006, 316: 447-458.

[8]Raul F,Soledad T. The Euler scheme for Hilbert space valued stochastic differential equations[J]. Statistics and probability Letters, 2001, 51: 207-213.

[9]Martin A S, Soledad T. Euler scheme for solutions of a countable system of stochastic differential equations[J]. Statistics and Probability Letters, 2001, 54: 251-259.

[10]Lepingle D.Euler scheme for reflected stochastic differential equations[J]. Mathematics and Computers in Simulation, 1995, 38: 119-126.

[11]Wang Wenqiang, Chen Yanping. Mean-square stability of semi-implicit Euler method for nonlinear neutral stochastic delay differential equations[J]. Applied Numerical Mathematics, 2001, 61: 696-701.

[12]Cao Wanrong, Zhu Mingzhu, Fan Zhencheng. Ms-stability of the Euler-Maruyama method for stochastic differential equations[J]. Applied Mathematics and Computation, 2004, 159: 127-135.

[13]Higham D J, Mao X, Stuart A M. Strong convergence of Euler-type methods for nonlinear stochastic differential equations[J].SIAM J Numer Anal, 2002, 40(3): 1041-1063.