带有领导者的多智能体避障队形控制
姚立强,宋艳荣,张术东
(1. 烟台大学数学与信息科学学院,山东 烟台 264005; 2. 海军航空工程学院系统科学与数学研究所,山东 烟台 264001)
多智能体系统的协同控制问题是多智能体系统研究的热点问题,协同控制问题研究主要集中在蜂拥控制问题[1]、一致性问题[2-3]、队形控制问题[4]以及群集控制问题[5].多智能体避障队形控制是指如何在有障碍物的环境中,智能体编队在运动过程中能安全、无碰撞地绕开所有障碍物,速度达到一致,且实现并维持预先指定的队形.队形控制广泛应用于民用工业领域和军事领域.
目前,多智能体系统队形控制方法主要有领导-跟随法[6]、基于行为法[7]、虚结构法[8]和势函数法[9].领导-跟随法既可以处理带领导者的多智能体系统问题,也可以将不带领导者的多智能体系统引入虚拟领导者,将问题转化为有领导者问题来处理.Olfati-saber运用这一思想在文献[10]中给出了具有单个虚拟领导者的蜂拥控制策略;Su Housheng[11]将Olfati-saber的结果进一步推广,提出了跟踪多个虚拟领导者的蜂拥控制策略.领导-跟随法虽然在多智能体控制研究中得到广泛应用,但在用于队形控制时大多不考虑障碍物的存在.本文研究在障碍物存在的情况下如何实现队形控制问题,同时要求多智能体既能避免相互之间发生碰撞,又能绕开障碍物.由于在实现队形的过程中要同时考虑避障和避碰问题,所以在运用领导-跟随法实现队形控制的基础上,引入势函数,实现避障和避碰问题.
本文主要运用人工势场法,借助改进后的避障势函数和避撞势函数,在文献[12]的基础上研究带有领导者的多智能体系统的队形控制及避撞、避障问题,给出了实现期望队形控制的控制策略的设计方法.
1 问题的提出
考虑由N+1个智能体组成的多智能体系统,其中有且只有一个领导者,该领导者具有如下所示的位置—速度模型
(1)
其中:q0∈Rn是领导者的位置向量,p0∈Rn是其速度向量,a0∈Rn是其加速度向量.
多智能体系统中其他N个智能体的地位是平等的,都是跟随者.假定第i(i=1,2,…,N)个跟随者具有如下的位置-速度模型
(2)
其中:qi∈Rn是跟随者i的位置向量,pi∈Rn是其速度向量,ui∈Rn是控制输入.
注1 领导者可以向每一个跟随者发送信息,跟随者能够接收来自领导者的信息且具有避撞感知、避障感知功能.
为了更好地描述多智能体系统的队形控制问题,我们引入以下定义.
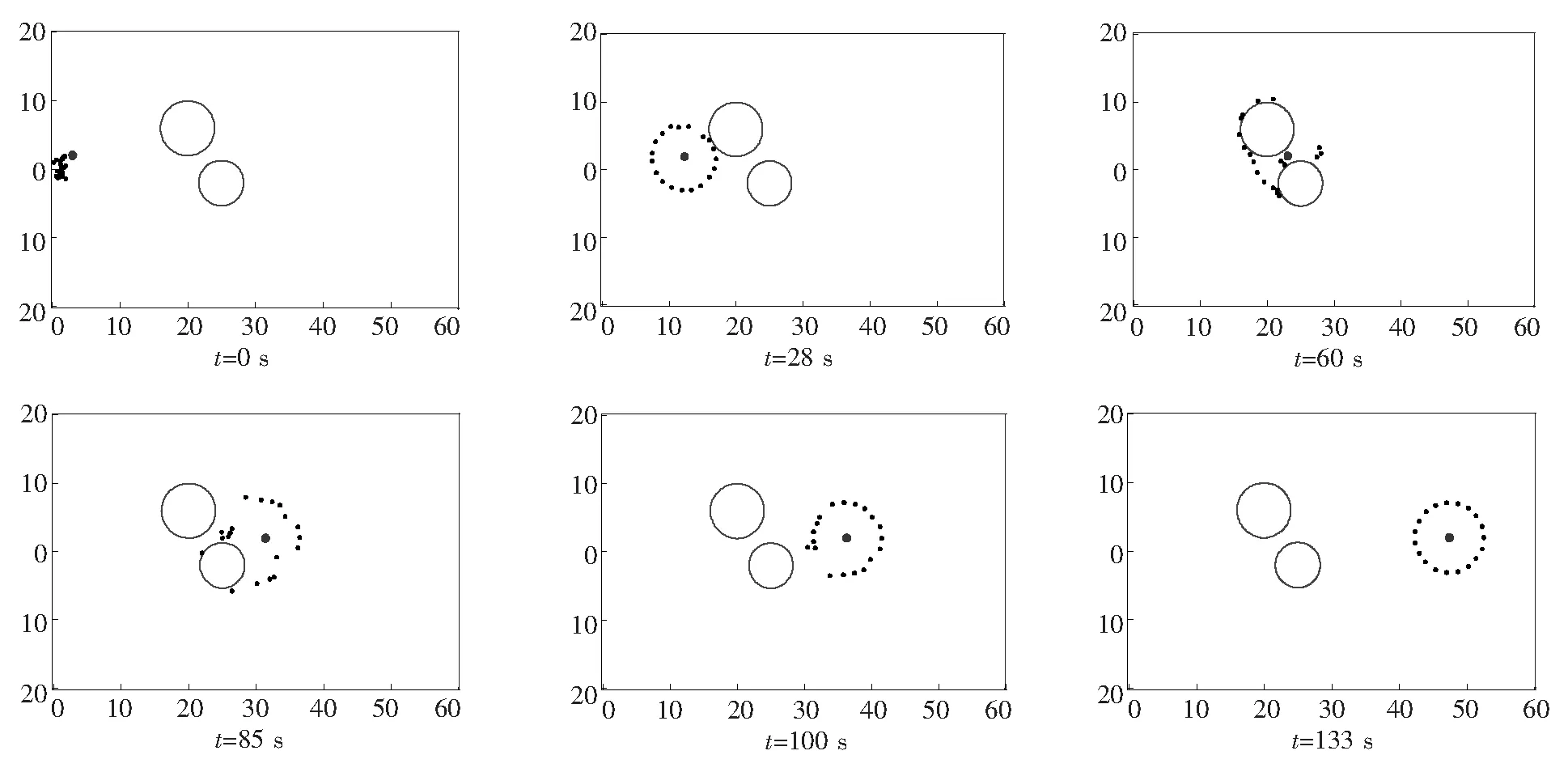
定义1[11](基于感知的跟随者的邻居集) 如果多智能体系统中的智能体j(包括领导者)位于跟随者i的避撞感知区域(以避撞感知半径Ri为半径的区域)内,即2个智能体的相对位置满足‖qi-qj‖ Nαi={j|‖qi-qj‖ (i=1,2,…,N) (3) 称为跟随者i的邻居集. 智能体之间的避撞控制目标用数学形式可以描述为 ∀t>0,‖qi(t)-qj(t)‖→/ 0. (i≠j;i,j=0,1,…,N) (4) 受Olfati-saber在文献[10]中对固定障碍物的处理方法的启发,我们给出径向K∞类函数的定义. 定义2(径向K∞类函数) 全平面上定义的二元连续可微函数F(x,y)在点(a,b)取得最小值0,如果满足 1) 对于固定的角度θ,F(a+rcosθ,b+rsinθ) (r≥0)是r的严格单调上升函数; 2) 对于固定的角度θ,当r→∞时,有F(a+rcosθ,b+rsinθ)→∞; 则称F(x,y)为以(a,b)为底的径向K∞类函数. 径向K∞类函数具有如下性质 (1) 对任意C>0,{(x,y):F(x,y)≤C}是一个单连通的有界闭区域,边界为F(x,y)=C. (2) 定义ρC(d)=min{‖X-Y‖:X∈BC,Y∈BC+d},则ρC(d)是d(d≥0)的单调递增函数. 注2 基于径向K∞类函数性质1,可以用形如{(x,y):F(x,y)≤C} (C>0)的集合来描述障碍物,障碍物边界用BC={(x,y):F(x,y)=c}表示. 注3 借助于径向K∞类函数的性质,智能体和障碍物之间的避障问题可以转换为障碍物边界曲线函数值与智能体位置向量在该边界曲线的等位线曲线上函数值之间的大小比较问题. 注4 假设系统中的领导者总是可以成功躲避障碍物. 下面,我们给出跟随者i相对于固定障碍物Ok的避障感知半径和避障作用区域的定义. 定义3(跟随者相对于障碍物的避障感知半径) 如果障碍物Ok对距离小于等于dik的跟随者i产生“排斥力”,即跟随者i采取避障动作,则称dik为跟随者i相对于障碍物Ok的避障感知半径. 定义4(障碍物相对于跟随者的避障作用区域) 对于给定的避障感知半径dik,区域Dik={(x,y):Ck 跟随智能体i的障碍物邻居集可以写为 Nβi={k|rik∈Dik;i=1,2,…,N;k=1,2,…,M}. 这里,rik=Fk(qi)是智能体i在障碍物Ok边界曲线的一条等位线上的函数值,Dik是跟随智能体i相对于障碍物Ok的避障作用区域,M是障碍物的个数. 跟随智能体i与障碍物Ok之间的避障控制目标可以描述为 ∀t>0,rik-Ck→/ 0. (i=1,…,N;k=1,2,…,M) (5) 定义5[12](期望队形) 期望队形就是某个向量h=col(h1,h2,…,hN),其中hi是跟随智能体i相对领导智能体的相对位置. 如果多智能体系统(1)和(2)中智能体i的位置向量满足 qi-q0=hi.(i≠j;i,j=1,2,…,N) (6) 则称多智能体系统实现期望队形h. 注5 期望队形中两智能体之间的距离总是大于它们的避撞感知半径. 因此,本文控制问题可以描述为:设计恰当的协作控制输入ui,使得多智能体系统(1)和(2)满足避撞控制目标(4)、避障控制目标(5)和队形控制目标(6). 本节主要研究在避撞、避障条件下设计控制策略,以实现期望队形.借助文献[12]中队形匹配势函数生成函数和避撞势函数生成函数,可以定义如下的队形匹配势函数和避撞势函数. 定义6(队形匹配势函数) 在多智能体系统(1)和(2)中,跟随者i的队形匹配势函数Vi(qi-q0,hi)是一个非负、连续可导的函数,且满足:1)Vi(qi-q0,hi)=0成立当且仅当qi-q0=hi;2) 当‖qi-q0-hi‖→∞时,Vi(qi-q0,hi)→∞. 要想实现避撞控制目标(4),应构造能够产生避撞的势函数. 跟随智能体i的总的避撞势函数 (7) 要实现避障控制目标(5),需构造躲避障碍物的避障势函数. 跟随者i总的避障势函数为 (8) 定理1 考虑一个由N+1个智能体组成的多智能体系统,其中有且仅有一个领导者,其余智能体为跟随者,系统中智能体的位置—速度模型为(1)和(2).假定系统在行进过程中至多会遇到M个外部环境中的固定障碍物Ok(k=1,2,…,M),领导者总是在障碍物的避障作用区域外活动,同时假设多智能体系统总的能量W0为一个有限值,则多智能体系统在控制输入(9)的作用下,最终会形成期望队形,且在运动过程中智能体之间不发生碰撞,并能成功避开障碍物,即同时实现避撞控制目标(4)、避障控制目标(5)和队形控制目标(6). (9) 其中: 证明定义多智能体系统(1)和(2)总的能量W为智能体系统总的队形匹配势函数、避撞势函数以及智能体与障碍物之间总的避障势函数之和,简称能量函数.它的表达式如下 (10) 从能量函数W的表达式可以知道该函数是一个半正定的函数,并且 (11) (12) 将式(12)代入控制输入(9)和能量函数(10)中,可得 (13) (14) 其中: (15) 进一步,将式(12)代入式(11)中得 (16) 由于 (17) (18) (19) (20) 将式(13)、式(17)~(20)代入式(16)中得 (21) (22) pi=p0.(i=1,2,…,N) (23) ▽qiVi(qi-q0,hi)=0. (24) 式(24)可以理解为,系统的队形匹配势函数对系统的作用力为零.由定义8可知 qi-q0=hi. (i=1,2,…,N) (25) 这样,由式(23)和(25)可知,在控制输入(11)的作用下,多智能体系统(1)和(2)能够实现预先给定的期望队形h,即实现队形控制目标(6). 下面,用反证法来证明多智能体系统在运动过程中,智能体之间不会发生碰撞. 假设系统中智能体r和e在时刻t1>0相撞,即智能体r和e在时刻t1的位置满足 qr(t1)=qe(t1). (r≠e;r,e=0,1,2,…,N) 由定义10和式(7)知 由于t=t1时,qr(t1)=qe(t1),所以根据定义10,当t→t1时 (26) 另一方面,由式(10)知 (27) 由于系统总的能量W0为有限值,这样式(26)和(27)产生矛盾.说明假设错误,多智能体系统在行进过程中智能体之间不会发生碰撞,即实现避撞控制目标(4). 同理,用反证法也可以证明系统在行进过程中可以成功躲避来自外部环境的固定障碍物,这里略过. 综上所述,在控制输入(9)的作用下,有领导者多智能体系统(1)和(2)可以实现避撞控制目标(4)、避障控制目标(5)和队形控制目标(6).证毕. 本节主要验证施加控制输入(11)后,多智能体系统(1)和(2)中的跟随者能够跟随领导者实现避撞控制目标(4)、避障控制目标(5)和队形控制目标(6). 仿真中系统的领导者在平面中沿平行于x轴的方向匀速向右移动,领导者和19个跟随者的初始位置在[0,2]×[-2,2]的区域内任意选取,初始速度随机生成,障碍物是2个以(20,6),(25,-2)为中心的圆.仿真的目标是跟随者在避撞、避障的前提下以领导者为圆心均匀排列在半径为5的圆周上行进.仿真图如图1所示. 图1 带领导者多智能体系统的运动轨迹图 由图1系统运动轨迹可以看出,在无障碍情形,系统中的跟随者排列在领导者周围逐渐形成期望队形 (如t=28 s所示);遇到障碍物后,跟随者暂时不考虑队形,以避障为主(如t=60 s,t=85 s所示);穿越障碍物后,跟随者再次与领导者形成期望队形 (如t=100 s,t=133 s所示). 本文利用势函数方法研究了带有领导者的多智能体在避撞、避障条件下的队形控制问题.通过构造队形势函数、避撞势函数以及避障势函数,给出了队形控制的控制策略,并证明了在该控制策略的作用下,系统能够实现期望的队形,并且避免了智能体之间碰撞的发生,成功躲避外部障碍物.最后,利用仿真说明了该方法的有效性. 参考文献: [1]Lu Xiaoqing, Austin F, Chen Shihua.Flocking in multi-agent systems with active virtual leader and time-varying delays coupling [J].Communications in Nonlinear Science and Numerical Simulation, 2011, 16(2): 1014-1026. [2]Hu Guoqiang. Robust consensus tracking of a class of second-order multi-agent dynamic systems[J].Systems & Control Letters, 2012, 61(1): 134-142. [3]Huang Qizhen. Consensus analysis of multi-agent discrete-time systems [J]. Acta Automatica Sinica, 2012, 38(7): 1127-1133. [4]Liu Yang, Jia Yingmin. An iterative learning approach to formation control of multi-agent systems [J]. Systems & Control Letters, 2012, 61(1): 148-154. [5]Ryan M R, Madey G R. Swarm control of UAVs for cooperative hunting with DDDAS [J]. Procedia Computer Science, 2013, 18: 2537-2544. [6]Cui Rongxin, Ge S S, How B V E, et al.Leader-follower formation control of underactuated autonomous underwater vehicles [J]. Ocean Engineering, 2010, 37(17-18): 1491-1502. [7]Liang Haizhao, Wang Jianying, Sun Zhaowei. Robust decentralized coordinated attitude control of spacecraft formation [J]. Acta Astronautica, 2011, 69(5-6): 280-288. [8]Cong Binglong, Liu Xiangdong, Chen Zhen. Distributed attitude synchronization of formation flying via consensus-based virtual structure [J].Acta Astronautica, 2011,68(11-12): 1973-1986. [9]Badawy A, McInnes C R. Small spacecraft formation using potential functions [J]. Acta Astronautica, 2009, 65(11-12): 1783-1788. [10]Olfati-saber R.Flocking for multi-agent dynamic systems: algorithms and theory[J]. IEEE Transactions on Automatic Control, 2006, 51(3): 401-420. [11]Su Housheng, Wang Xiaofan, Lin Zongli. Flocking of multi-agents with a virtual Leader [J].IEEE Transactions on Automatic Control, 2009, 54(2): 293-307. [12]姚立强,宋艳荣,张术东.基于势函数的多智能体避撞队形控制[J].烟台大学学报:自然科学与工程版,2014, 27(1):45-49.2 控制策略的设计
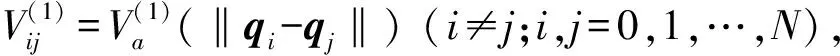





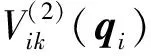
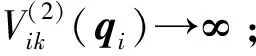
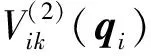
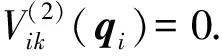
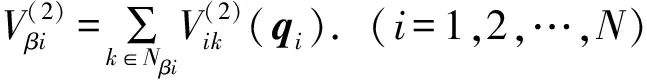
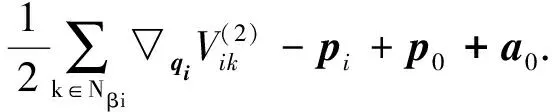
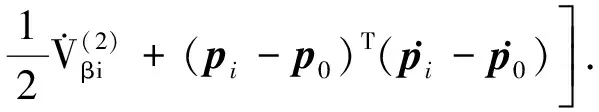

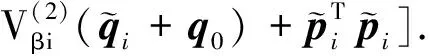

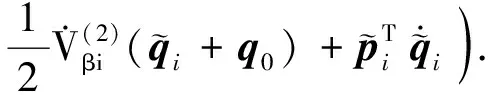

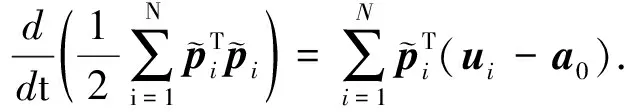


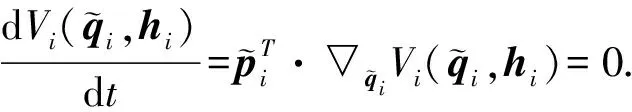
3 仿真实例
4 小 结
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

