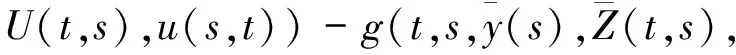Lévy过程驱动的倒向重随机Volterra积分方程的对称解
刘存霞,吕 文
(烟台大学数学与信息科学学院, 山东 烟台 264005)
在全局Lipschitz条件下, Pardoux 和 Peng[1]证明了非线性的倒向随机微分方程(简记为:BSDE)解的存在唯一性. 自创立至今, 倒向随机微分方程在理论和应用方面均取得了巨大成果[2-4]. 在文献[5]及[6]中,作者通过建立与 Lévy 过程相关的鞅表示定理研究了一类 Lévy过程驱动的 BSDE, 在全局 Lipschitz条件下证明了适应解的存在唯一性定理. 在此基础上, Bahlali等[7]讨论了由布朗运动和 Lévy 过程共同驱动的 BSDE,在全局 Lipschitz 条件下建立了解的存在唯一性定理. Lin[8]研究了一类特殊形式的倒向随机 Volterra 积分方程(简记为: BSVIE):


(1)
这一工作源自于Hu和Peng[9]对 Hilbert空间中的半线性倒向随机发展方程的研究. 接着, Yong[10]讨论了以下形式的BSVIE:


(2)
作者给出了解的存在唯一性以及在动态风险测量和最优控制中的应用. 文献[11]证明了一类由 Lévy过程驱动的倒向重随机微分方程适应解的存在唯一性并给出了在随机偏微分方程中的一个应用.基于以上工作, 文献[12]对一类由Lévy过程驱动的倒向重随机Volterra积分方程(简记为:BDSVIEL), 给出了解的存在唯一性定理.
另外, 在文献[10],[13]及[14]的研究基础上, Wang 和 Shi[15]针对方程(2)提出了倒向随机Volterra 积分方程对称解 (简记为S-解). 区别于传统的 M-解, 倒向随机 Volterra积分方程对称解的一个主要特征是要求扩散项系数Z(·,·)关于时间变量是对称的, 即Z(t,s)=Z(s,t).
本文将在文献[12]的基础上,讨论一类更一般的由Lévy过程驱动的倒向重随机Volterra积分方程,在系数满足全局Lipschitz条件的假设下,利用不动点定理证明对称解的存在唯一性定理. 为此,首先给出一些基本的记号以及假设等基础知识,本文第二部分将给出对称解的存在唯一性定理.
1 预备知识
给定实数T>0, 设(Ω,F,P)为一概率空间, 假设 {Bt:t∈[0,T]} 和 {Wt:t∈[0,T]}是其上定义的两个相互独立的实值标准布朗运动;Lt=bt+lt为一实值Lévy过程且满足以下条件:
(ii)对每个ε>0及任意的λ>0,
对∀(t,s)∈[0,T]2, 令
对任意的R,S∈[0,T] 且R Δc={(t,s)∈[R,S]2;t≤s}, Δ={(t,s)∈[R,S]2;t>s}. 首先给出以下空间: 对任意的 0≤R ‖(y(·),z(·,·),u(·,·))‖H2[R,S]:= ‖(y(·),z(·,·),u(·,·))‖*H2[R,S]:= 对给定的 Lévy 过程 {Lt:t∈[0,T]}, 定义一族与Lt相关的随机过程(H(i))i≥1如下: 本文将讨论以下形式的 BDSVIEL: Z(s,t),U(t,s),U(s,t))ds+ (3) 其中:系数f,g:Δc××d×d×l2×l2→均为B(Δc×m×m×d×m×d)⊗FT-可测且满足: (A1) 对任意的 (t,y,z,z',ζ,ζ')∈[0,T]××d×d×l2×l2,映射s→f(t,s,y,z,z',ζ,ζ') 以及s→g(t,s,y,z,z',ζ,ζ') 均为F-循序可测且 (4) 其中:f0(t,s)≡f(t,s,0,0,0,0,0),g0(t,s)≡g(t,s,0,0,0,0,0). (A2) 对∀(t,s)∈ [0,T]2,(yi,zi,ηi,ui,γi)∈×d×d×l2×l2,i=1,2, 存在常数K>0,α,β>0 且α+β<1使得 |f(t,s,y1,z1,η1,u1,γ1)-f(t,s,y2,z2,η2,u2,γ2)|2≤ K(|y1-y2|2+|z1-z2|2+|η1-η2|2+ |u1-u2|2+|γ1-γ2|2), |g(t,s,y1,z1,η1,u1,γ1)-g(t,s,y2,z2,η2,u2,γ2)|2 ≤K|y1-y2|2+α(|z1-z2|2+|u1-u2|2)+ β(|η1-η2|2+|γ1-γ2|2). 本节将给出BDSVIEL(3)S-解的存在唯一性. 为此, 先考虑 BDSVIEL(3)的一个特殊形式. 对任意的t∈[R,T],r∈[S,T],记 (5) 其中:系数f,g: [R,T]×[S,T]×d×l2→满足简化形式的假设 (A1),(A2). 显然, 方程 BDSVIEL(5) 是一族以t为参数的 Lévy过程驱动的倒向重随机微分方程, 由文献[11]中的定理 4,有以下引理: 接下来,考虑 BDSVIEL(5) 的两个特殊情形. 情形 1 取R=S, 定义 (6) 则 BDSVIEL(5)可记为 (7) 有以下引理: 证明由文献[12]中定理 1知, BDSVIEL(7) 存在唯一的适应解 (Y(·),Z(·,·),U(·,·))∈H2[S,T]. 对任意的 (t,s)∈Δ, 定义Z(t,s)=Z(s,t) 以及U(t,s)=U(s,t), 即得 BDSVIEL(7)存在唯一的S-解. 引理得证. 情形2 在BDSVIEL(5)中,令r=S∈[R,T],对任意的t∈[R,S],s∈[S,T],定义 (8) 从而有 (9) 由引理2,有以下引理: 下面讨论一般形式的 BDSVIE(3). 证明首先证明对给定的S∈[0,T],BDSVIEL(3)在[S,T]上存在唯一的S-解. 对任给的S∈[0,T], 记 M2[S,T]:={(y(·),z(·,·),u(·,·)) | (y(·), z(·,·),u(·,·))∈*H2[S,T] 且z(t,s)=z(s,t),u(t,s)=u(s,t), ∀(t,s)∈[S,T]2,a.s.} 易证M2[S,T]是*H2[S,T]的一个非空闭子集. z(s,t),U(t,s),u(s,t))ds+ (10) 由引理2知,上述BDSVIEL存在唯一的S-解(Y(·),Z(·,·),U(·,·))∈M2[S,T]. 定义映射Φ:M2[S,T]→M2[S,T] Φ(y(·),z(·,·),u(·,·))= (Y(·),Z(·,·),U(·,·)) (11) 下证对合适的S, 当T-S>0 充分小时, 映射Φ是压缩的. 由基本不等式,有 y(s),Z(t,s),z(s,t),U(t,s),u(s,t))- f(t,s,y(s),Z(t,s),z(s,t),U(t,s),u(s,t))- Z(t,s),z(s,t),U(t,s),u(s,t))- 由系数的Lipschitz 假设, 经简单计算得 对上述不等式在区间 [S,T] 上积分可知, 当T-S>0充分小时,我们可以选择足够小的θ>0使得映射Φ是压缩的. 从而BDSVIEL(3)在[S,T]上存在唯一的S-解. 进一步地,对t∈[R,S], 考虑以下方程: z(s,t),U(t,s),u(s,t))ds+ (12) 参考文献: [1]Pardoux E, Peng Shige. Adapted solution of a backward stochastic differential equation[J]. Systems Control Lett, 1990,14: 55-61. [2]El Karoui N, Peng Shige, Quenez M. Backward stochastic differential equations in finance[J]. Math Finance,1997, 7: 1-71. [3]Peng Shige.Backward stochastic differential equations and its application in optimal control[J]. Appl Math Optim,1993, 27: 125-144. [4]Hamadene S, Lepeltier J. Zero-sum stochastic differential games and backward stochastic differential equations[J]. Systems Control Lett, 1995, 24: 259-263. [5]Nualart D, Schoutens W. Chaotic and predictable representations for Lévy processes[J]. Stochastic Process Appl, 2000, 90: 109-122. [6]Nualart D, Schoutens W. Backward stochastic differential equations and Feynman-Kac formula for Lévy processes, with applications in finance[J]. Bernoulli, 2001, 7: 761-776. [7]Bahlali K, Eddahbi M, Essaky E. BSDE associated with Lévy processes and application to PDIE[J]. Journal of Applied Mathematics and Stochastic Analysis, 2003, 16: 1-17. [8]Lin Jianzhong. Adapted solution of backward stochastic nonlinear Volterra integral equations[J]. Stochastic Ana Appl, 2002, 20: 65-183. [9]Hu Ying, Peng Shige. Adapted solution of backward semilinear stochastic evolutin equation[J]. Stochastic Analysis and Applications, 1991, 9: 445-459. [10]Yong Jiongmin. Backward stochastic Volterra integral equations and some related problems[J]. Stochastic Proc Appl,2006, 116: 779-795. [11]Ren Yong, Lin Aihui, Hu Lanying. Stochastic PDIE and backward stochastic differential equations driven by Lévy processes[J]. J Comp Appl Math, 2009, 223: 901-907. [12]刘存霞, 吕文. Lévy过程驱动的倒向重随机Volterra积分方程[J].烟台大学学报:自然科学与工程版, 2012, 25(3): 157-161. [13]Yong Jiongmin. Continuous-time dynamic risk measures by backward stochastic Volterra integral equations[J]. Appl Anal, 2007, 86: 1429-1442. [14]Yong Jiongmin. Well-posedness and regularity of backward stochastic Volterra integral equation[J]. Probab Theory Relat Fields, 2008, 142: 21-77. [15]Wang Tianxiao, Shi Yufeng. Symmetrical solutions of backward stochastic Volterra integral equations and their applications[J]. Discrete and Continuous Dynamical Systems Series B, 2010, 14: 251-274.
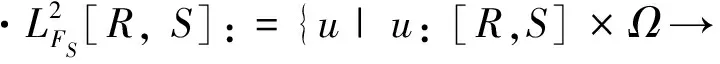
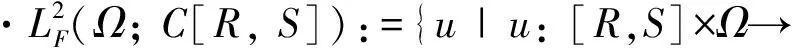
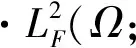
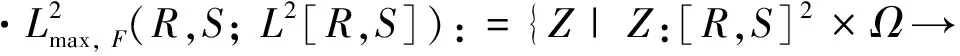
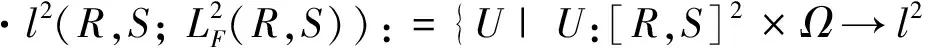

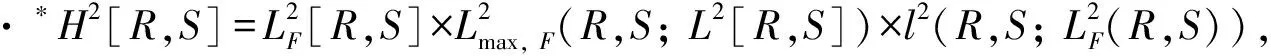
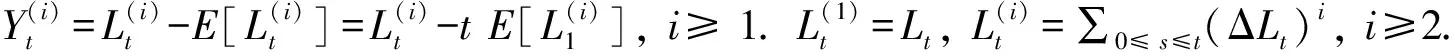



2 主要结果