抛光机磨削加工效率的试验研究

迟明善,王仲文,邵俊鹏,徐晓秋

(1.哈尔滨理工大学荣成学院,山东 荣成 264300;2.哈尔滨理工大学机械动力工程学院,黑龙江 哈尔滨150080)

在瓷质砖的深加工阶段,为了获得更好的表面光洁度,抛光磨削技术得到广泛的应用．然而,随着陶瓷厂对日生产量的要求不断提高,导致每条深加工生产线上需要的抛光磨头的数目以及磨削加工的时间也逐渐增多,这就大大提高了生产成本．因此,为了保证在日生产量不变的前提下,降低生产成本,就需要对影响抛光加工效率的因素展开研究分析．为了解决上述问题,文献[1]在描述抛光机磨削运动的基础上,利用Matlab软件对该运动进行仿真分析;文献[2]则在大平面机械抛光运动分析基础上,综合磨削速度、磨削时间共同影响,建立平面磨削均匀性模型并进行仿真分析;文献[3]以墙地砖打蜡机为原型,建立抛光磨削均匀性数学模型并对其影响因素进行分析与模拟仿真．然而,所有的上述研究都针对抛光过程或者是磨削均匀性提出数学模型并进行验证,但未涉及到对影响抛光磨削效率的各因素的研究分析．因此,本文在分析抛光磨削运动的基础上,结合Preston方程得出影响抛光磨削的因素,并利用正交试验的方法对影响因素进行研究分析,确定各影响因素的主次关系以及各自的变化趋势,得出磨削加工的最佳组合形式,从而为指导生产加工以及后续研究提供理论依据．

1 抛光磨削运动分析

以JP800/16型抛光机为例,该系列的抛光机横梁上等距分布16个抛光磨头,每个磨头的圆周方向上又均布6个摆动磨块．当进行磨削加工时,抛光机传送带以一恒定速度承载瓷质砖运动,其上的横梁又通过齿轮齿条机构带动磨头左右往复摆动,如图1所示．

图1 抛光机磨削加工示意图

与此同时,抛光磨头绕各自主轴高速旋转,并利用其内部的两齿差行星齿轮传动机构便驱动凸轮产生相对于磨头座自转的相对运动,其具体传动关系如图2所示．此时,凸轮的端面轮廓便驱动圆周方向均匀分布的3个主动摆杆上的磨块左右往复摆动,3个主动摆杆再带动交错分布的3个从动摆杆的磨块运动,从而达到磨块对砖坯的线接触式磨削的目的．

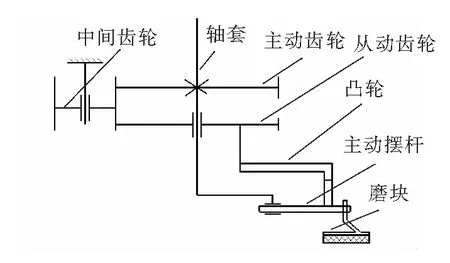
图2 摆杆机构传动示意图

在整个磨削加工的过程中,横梁还通过安装在其上的气缸对整个磨头施加恒定的工作压力[4-5]．

2 抛光磨削影响因素的分析

Preston方程是广泛应用在磨削加工中的公式,此方程是由Preston在1927年提出的．在一定条件下,可以采用Preston方程描述磨粒加工对工件的去除量与各种参数以及磨粒特性的关系．在Preston方程中,将磨粒的速度和磨粒对磨面压力外的所有因素都归结为一个比例常数kp,称为Preston常数,得

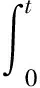
(1)

式中:Δz为磨削去除量;v为磨粒在近壁区的相对运动速度;p为磨粒在近壁区的相对压力;kp包括了与磨粒本身相关的部分因素(磨粒的大小、形状和硬度)、磨粒与壁面发生作用时的因素(磨粒与壁面的撞击角度)以及被加工工件自身因素(被加工件的硬度)等[6-7]．

在瓷质砖的抛光磨削加工过程中,加工对象——瓷质砖保持不变,磨粒与砖表面的撞击角度又近似不变,因此kp值仅与磨块的种类有关,而磨块的种类是按其磨料粒度的大小来进行分类的,并以目数来表示,目数越大,表明磨粒的颗粒越细;p为在加工过程中,磨粒对瓷质砖表面施加的压力,在此近似等于气缸对抛光磨头施加的恒定压力;v为参与加工磨粒与瓷质砖接触表面的相对速度,随磨块上工作点位置的变化而变化,该速度是由抛光磨头自身旋转的速度、磨块往复摆动的速度、横梁摆动的速度以及传送带运动的速度的合成．由于在实际的磨削加工过程中,传送带的速度以及磨块往复摆动的速度很小,故在此忽略不计．因此,在抛光磨削t时间内,每个磨块的总磨削量H为

(2)

式中:n为磨块上参与磨削加工的磨粒数目．由于在同一个抛光磨头中,其圆周方向的6个磨块是均匀分布的,并且所使用的磨块也是材料、结构都完全相同的,因此在磨削加工过程中,每个磨块上参与加工的磨粒数目是相同的．故当磨削加工时间为t时,一个抛光磨头的总磨削量为6H．

通过上述分析可以看出:在相同的磨削加工时间内,抛光磨头的总磨削量只取决于kp,p,v,即磨块的目数、工作压力、磨头的转速以及横梁的摆动速度．因此,上述4个因素即为影响抛光磨削加工的主要因素．

由图2可知，京津冀、长三角和珠三角城市群的地区生产总值与城镇居民生活用电量趋势基本一致。下面对三大典型城市群的城镇人口规模、居民收入水平、能源消费强度和产业结构等因素与城镇居民生活用电量进行分析:

3 正交试验设计

3.1 正交试验表及试验结果

为了探讨磨块目数、工作压力、磨头的转速以及横梁的摆动速度这4个因素对抛光磨削加工效率的影响,我们采用试验分析的方法．假定每个影响因素各取4个水平,若全面组合试验,则至少需要44次试验．为此,我们采用正交试验法L16(45)来安排试验,可以在不影响全面了解诸多因素对性能指标影响的条件下,大大减少试验次数,从而避免了根据主观经验减少考虑因素或试验次数的盲目性和试验结果无代表性的缺点．同时,采用正交设计法可以对影响陶瓷抛光磨削的各种因素进行方差分析,得出显著性的影响因素以及每个影响规律的变化趋势图[8-10]．

为了消除抛光机性能以及磨头自身质量等因素对试验结果的影响,采用同一台抛光机上的同一个抛光磨头进行抛光磨削加工试验;加工对象——瓷质砖统一采用某陶瓷厂生产的毛坯砖,如图3所示．设计试验时,采取磨块目数、工作压力、磨头转速和横梁的摆动速度4个因素,各因素所取的水平数如表1所示．其中,横梁摆动的幅度相同并且速度的大小用驱动电机的频率来表示;工作压力是用气缸内的压强来表示的．根据表1所示的因素水平和正交设计表L16(45),得出抛光磨削因素的组合表如表2所示．

图3 磨削试验装置图

表1正交试验因素水平表

Tab.1 Factors and levels of orthogonal test

水平因素转速/(r·min-1)压力/MPa目数/目摆速/Hz123442747552257022.63.248024032010000203040

在保证其他因素都不变的前提下,按照表1所示的各水平以及表2所示的各试验因素组合形式来安排磨削加工试验．试验开始前,先测量并记录瓷质砖加工前的重量并按照表2将抛光机的各因素调到相应水平．

表2 正交试验安排表

由于在实际磨削加工过程时,传送带运动的速度很小,故在此忽略不计(传送带保持静止状态)．试验结束后,将加工后的瓷质砖晾晒数日,待砖体完全干透后,测量磨削后的总质量,从而得到在此次试验中的磨削量．为了减少试验过程中产生的随机误差,每组试验因素组合重复3次,分析处理时取3次磨削量的平均值．具体的正交试验结果记录在表3中．

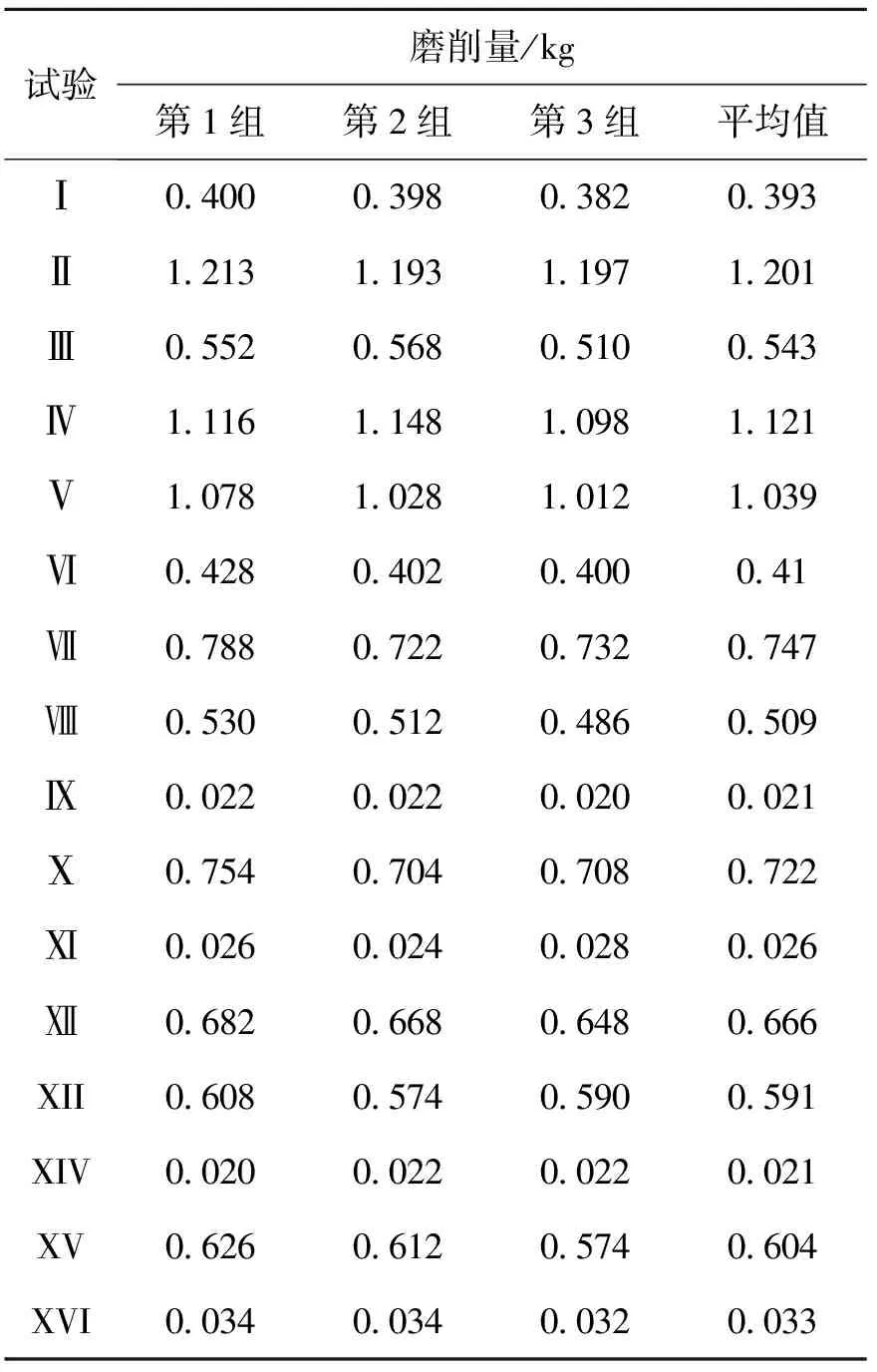
表3 正交试验结果记录表

3.2 正交试验结果分析

对试验结果进行方差分析,其目的是通过数据分析找出对该指标有显著影响的因子以及影响因子的最佳水平等．对于完全正交表Ln(tm)而言,用到的极差分析的数学理论为:Mj是影响因素在第j水平下4次试验的数据和;相关的方差分析的数学计算公式如下.

1) 总波动平方和

(3)

2) 各列波动平方和

(4)

式中:Ti为因子的第i水平试验结果之和,t为因素的水平个数,m为正交表列数,r=n/t．

3)F检验

采用F检验来确定哪个因子对结果影响显著:由于Sj与Se独立,在一个因子的效应均为0时,有

(5)

式中:MSj=Sj/fj为因子的均方和;fj=q-1为对应因子的自由度;MSe=Se/fe为误差的均方和,fe为误差的自由度．

当Fj>F1-α(fj,fe)时,认为在显著水平α上因子是显著的,其中F1-α是相应自由度的F分布的1-α分位数．α通常取0.05或0.01,并规定:当Fj>F0.95(fj,fe)时,该因子高度显著;当F0.95(fj,fe)≥Fj≥F0.90(fj,fe)时,该因素显著,记为(*);当Fj≤F0.90(fj,fe)时,该因素不显著[11]．

根据表3的试验数据,结合上述公式,对试验结果进行分析,具体结果记录在表4中．其中F0.95(3,3)=9.28,F0.90(3,3)=5.39．

针对每个影响因素,以水平数为横坐标,磨削量值为纵坐标,建立各影响因素的水平指标图,如图4所示．

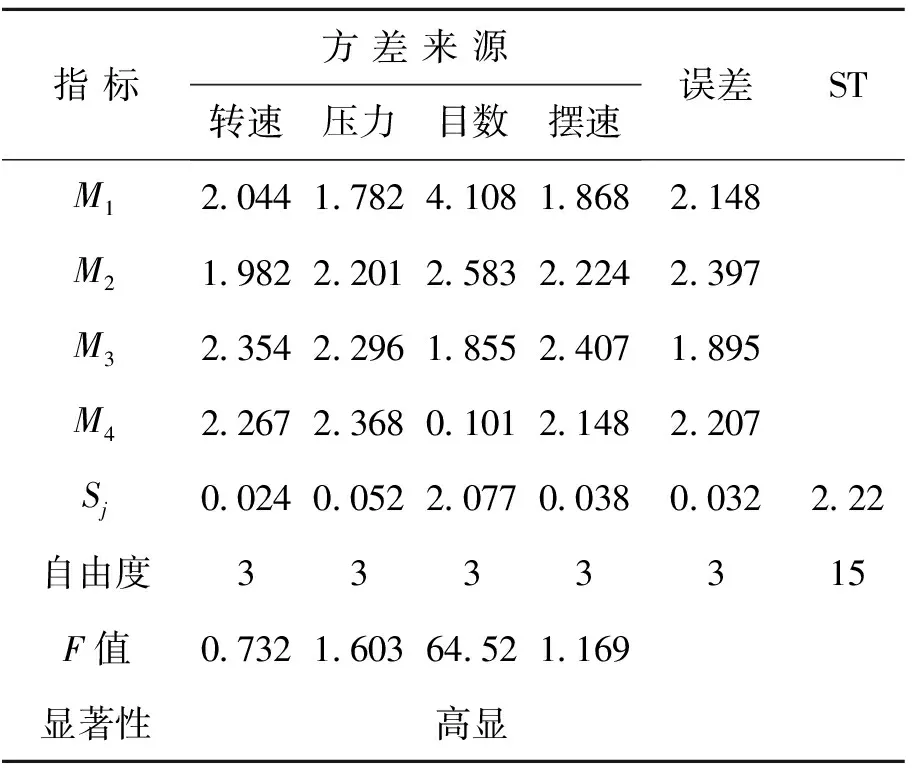
表4 正交试验分析表

从表4的正交试验分析表,可以看出:在抛光磨削阶段,磨块目数对抛光磨削效率的影响是最显著的,其他影响因素的主次关系依次是,压力、摆动速度和转速．而从图2所示的各影响因素的水平指标图上可以看出:1、磨头的转速对磨削效率的影响近似呈增长趋势的波浪形曲线,当转速在第三水平(522 r·min-1)时,此时的指标最高;2、压力对磨削效率的影响是逐渐增大的,但是当压力大于2.6 MPa时,增长的幅度减缓;3、磨块目数对磨削效率的影响是逐渐下降的,80目时的对应的指标最高;4、摆动速度对磨削效率的影响是比较平缓的,且各个水平的波动量不大,当频率为30 Hz时效率最高．

图4 各影响因素的水平指标图

4 结 论

(1)利用Preston方程从理论上分析了影响抛光磨削效率的因素,即磨头转速、压力、磨块目数以及横梁摆动速度．

(2)通过进行正交试验,确定影响因素的主次关系依次为:磨块目数、压力、摆动速度和转速,并且磨块目数对磨削效率的影响远远超出其他3个因素．

(3)对瓷质砖进行抛光磨削的目的就是为了获得更好的表面光洁度,因此在采用不同目数的磨块对瓷质砖进行粗、精加工时,可将其他3要素设定为:磨头的转速为522 r·min-1,压力设定为2.6 MPa,摆动的频率为30 Hz,以获得较佳的磨削效率．

参考文献:

[1]温革,王振林,向明,等.基于Matlab陶瓷墙地砖抛光运动模拟分析[J].陶瓷学报,2004,25(4):239-244.

[2]陈彩如,谭建平.大规格陶瓷砖抛光过程仿真与试验研究[J].中国陶瓷,2008,44(2):45-48.

[3]许雄超,王世旺.基于陶瓷抛光机抛磨运动建模及试验研究[J].机械设计与制造,2008,211(9):132-136.

[4]迟明善,邵俊鹏,王仲文.抛光磨头摆动机构建模与运动仿真[J].哈尔滨理工大学学报,2012,17(5):29-34.

[5]迟明善.抛光磨头凸轮轮廓设计与运动仿真[D].哈尔滨:哈尔滨理工大学,2011:3-20.

[6]Preston F W. The theory and design of plate glass polishing machines [J]. Journal of the Society of Glass Technology, 1927(11): 214-256.

[7]计时鸣,李琛,谭大鹏,等.基于Preston方程的软性磨粒流加工特性[J].机械工程学报,2011,47(17):156-163.

[8]Luo JianFeng, David A D. Material removal mechanism in chemical mechanical: Theory and modeling [J],IEEE Transactions on Semiconductor Manu-facturing, 2001,14(2):112-133.

[9]李丽霞,曲复宁,由翠荣,等.应用正交设计方法筛选牡丹愈伤诱导培养基的研究[J].烟台大学学报:自然科学与工程版,2005,18(1):41-49.

[10]Huang Mingfong, Lin Tsannrong, Chiu Huanchung. Effect of machining characteristics on polishing ceramic blocks [J]. The International Journal of Advanced Manu-facturing Technology, 2005, 26:999-1005.

[11]吴翊,李永乐,胡庆军.应用数理统计[M].国防科技大学出版社,1999:235-262.