广义阻尼边界条件下Laplace方程反问题的非线性积分方程法

胡宇清

(东南大学数学系，211100，南京)

0 引言

在科学研究中经常要通过间接观测来探索位于不可达、不可触之处的物质的变化规律;生产中经常要根据特定的功能对产品进行设计，或按照某种目的对流程进行控制。简而言之，就是由果索因，而这就是所谓的反问题。反问题大量出现于医学成像、地质探测、非损伤性探测、雷达遥感等领域。反问题不仅是非线性的，而且从数值计算的角度看是不适定的。

热成像、静电成像等很多物理问题在数学上被看做Laplace方程的逆边值问题，本文考虑这类问题的广义阻尼边值条件(GIBC)。目前对广义阻尼边界条件问题已有很多研究[1－3]。对于双连通区域已知外部边界上一些柯西数据重构内部边界形状的反问题通常采用文献[4]中提出的边界积分方程方法。边界积分方程方法已被广泛应用，文献[5，6]中作者应用该方法重构了腐蚀探测问题中被腐蚀边界的形状以及阻尼系数;文献[7]中作者对已知的腔体内部一条曲线上若干散射场的测量数据，运用该方法重构了外部腔体的形状。本文基于文献[4]中提出的方法通过格林公式定理推导出边界积分方程组，从而将要解决的重构边界形状反问题转化为了求解非线性积分方程组的问题，再用正则化的迭代方法最终重构出边界形状。

1 问题的叙述

假设双连通有界区域D⊂R2，其边界由2个非连接的光滑若当闭曲线Γ0和Γ1组成，使得∂D∶ =Γ0∪Γ1且Γ0∩Γ1=φ，其中Γ1是环形区域D的内边界。定义υ为区域D的边界单位外法向量。考虑如下边值问题:对给定的函数(Γ0)，u∈H2(D)满足

其中:divΓ1和 gradΓ1分别为表面散度和梯度，λ∈C1(Γ1)非负且不恒为0，μ∈C1(Γ1)为正。

假定边界Γ0上Dirichlet数据f对应的Neumann数据

是已知的。要考虑的反问题为:假设已知边界Γ1上阻尼系数，由Γ0上的一组柯西数据

1(Γ0)×H2(Γ0)重构边界Γ1的形状。在二维情况下，边界条件中的Laplace-Beltrami微分算子有表达式为切向导数，s为弧长。尽管这类反问题解的唯一性是未知的，但本文提出的数值反演方法仍然能很好地得到重建结果。

2 非线性积分方程

先从格林公式出发得到与原来反问题等价的非线性积分方程。根据Laplace方程的基本解

它们限制在部分边界上的形式为

其中，j，k=0，1。

对边值问题(1)的解u∈H2(D)，令α∶ =u|Γ1并简记

由格林公式[8]得到

在上式中令x由D的内部分别接近边界Γ0和Γ1，根据双层位势在边界上的跳跃关系可得积分方程

和

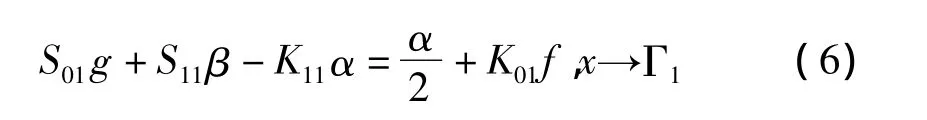
因此，要求的边界形状重构问题就转化为了由上式2个非线性方程组求解Γ1和α的问题。式(5)、式(6)是典型的非线性不适定积分方程组，这2个式子对于边界Γ1都是非线性的，对于α都是线性的。求解式(5)和式(6)的步骤是首先利用Frechet导数把非线性方程组近似表示为其线性形式，再用Tikhonov正则化方法处理问题的不适定性。

有3种迭代法求解非线性积分方程组(5)、(6)。

1)从式(5)中由线性方程解出α，代入式(3)得到β，然后关于未知边界Γ1线性化方程(6)，从而迭代更新得近似边界形状。

2)从式(6)出发，计算出α再代入式(3)得到β，对边界Γ1线性化方程(5)迭代更新得到近似边界形状。

3)将式(5)、式(6)关于边界Γ1和α同时线性化，解这2个方程，得到关于Γ1和α的更新迭代。文中将采用第3种迭代方法重构得到近似边界形状。

3 积分方程离散和迭代法

不失一般性，假定C2边界Γ0，Γ1的参数化形式分别为

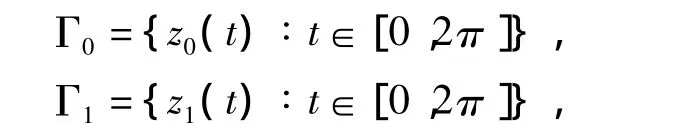
其中，z0∶R→R2，z1∶R→R2为以2π 为周期的 C2光滑函数。对任意一个向量a=(a1，a2)定义a⊥=(a2，－a1)为向量a顺时针旋转90°。令ψ=φ◦zj，j=0，1，根据单双层位势算子定义得对应的离散化的积分算子形式分别为

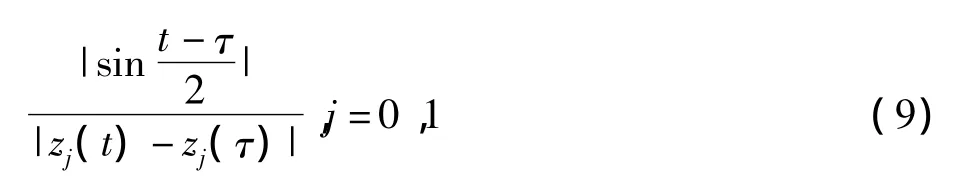
式(9)中第2项的对角线元素为

将式(5)、式(6)关于未知数Γ1和α完全线性化得到

1)给出未知边界Γ1的初始参数化估计z1。已知边界Γ1上阻尼系数λ，μ以及Γ0上的柯西数据f，g利用式(5)得到α，从而由式(3)计算出β。

2)将α，β以及边界初始估计z1代入式(10)和式(11)，解线性方程组得γ，ζ，从而得到更新α+ γ，z1+ ζ。

3)重复第2步直到满足迭代终止条件。下面给出Frechet导数的计算形式。

式(14)第1项和第3项中核的对角线元素为

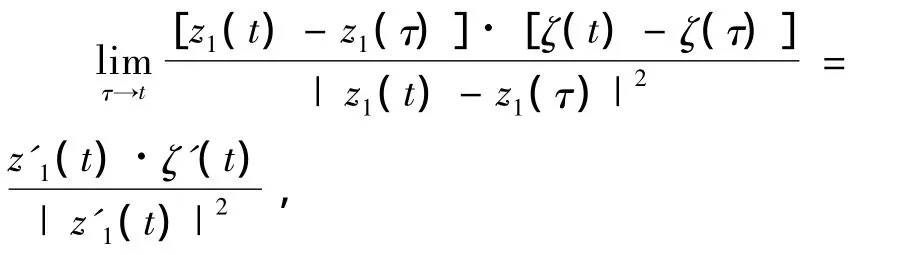
第2项和第4项核的对角线元素可由式(8)得到。

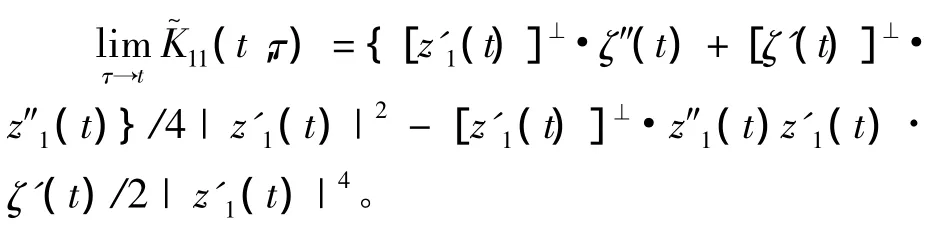
ω关于z1的Frechet导数为

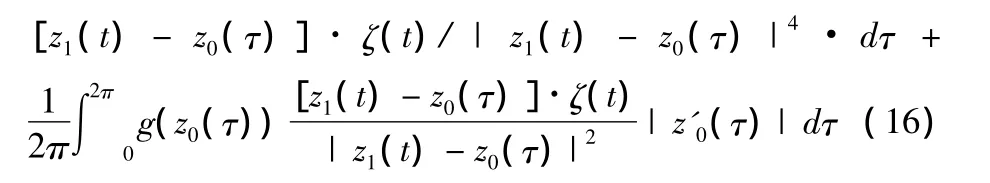
式(12)～式(16)中 t∈[0，2π]。下一节就将上述迭代法给出具体算例。

4 数值算例

根据文献[3]中介绍的利用单层位势在边界上的跳跃关系由已知边界上的Dirichlet数据算出Neumann数据，以下重构边界形状的数值算例都只用一组柯西数据，然后用积分方程方法重构内部边界形状。

将边界Γ1的更新记做

其中，q为非负函数。假设q可由如下三角多项式的形式来近似

在所有数值算例中外部的已知曲线Γ0为圆心在原点半径为0.9的圆，Γ1的初始估计为圆心在原点半径为0.8的圆，配置点个数为n=32，Γ1上三角多项式的展开系数取m=6。记αγ，αζ分别为γ以及边界更新ζ的正则化参数，it记为迭代步数。为了检验该迭代算法的稳定性，给测量数据g加上误差，误差数据由如下式子给出

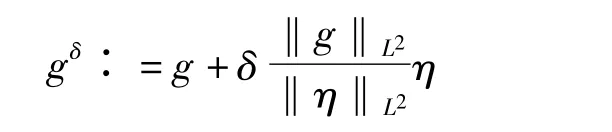
其中，η是正态分布随机变量，δ是相对噪音水平。

例1:考虑椭圆边界，其参数化形式为

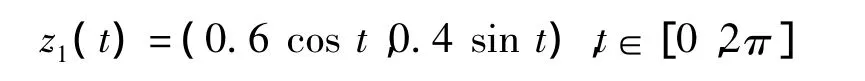
给定Dirichlet数据f(z0(t))=1。运用上述的正则化迭代法得到图1的重构结果。

图1中左图选取的正则化参数为αγ=10－2，αζ=10－1，迭代步数it=7。图1中右图选取的正则化参数为 αγ=10－2，αζ=10－2，迭代步数 it=9。图1中边界Γ1上阻尼系数取常数λ=2，μ=2，下面考虑阻尼系数为连续函数的情况。取λ=，Dirichlet数据仍为 f(z0(t))=1，得到图2所示重构结果。

图1 用精确测量数据和6%扰动数据重构椭圆边界形状

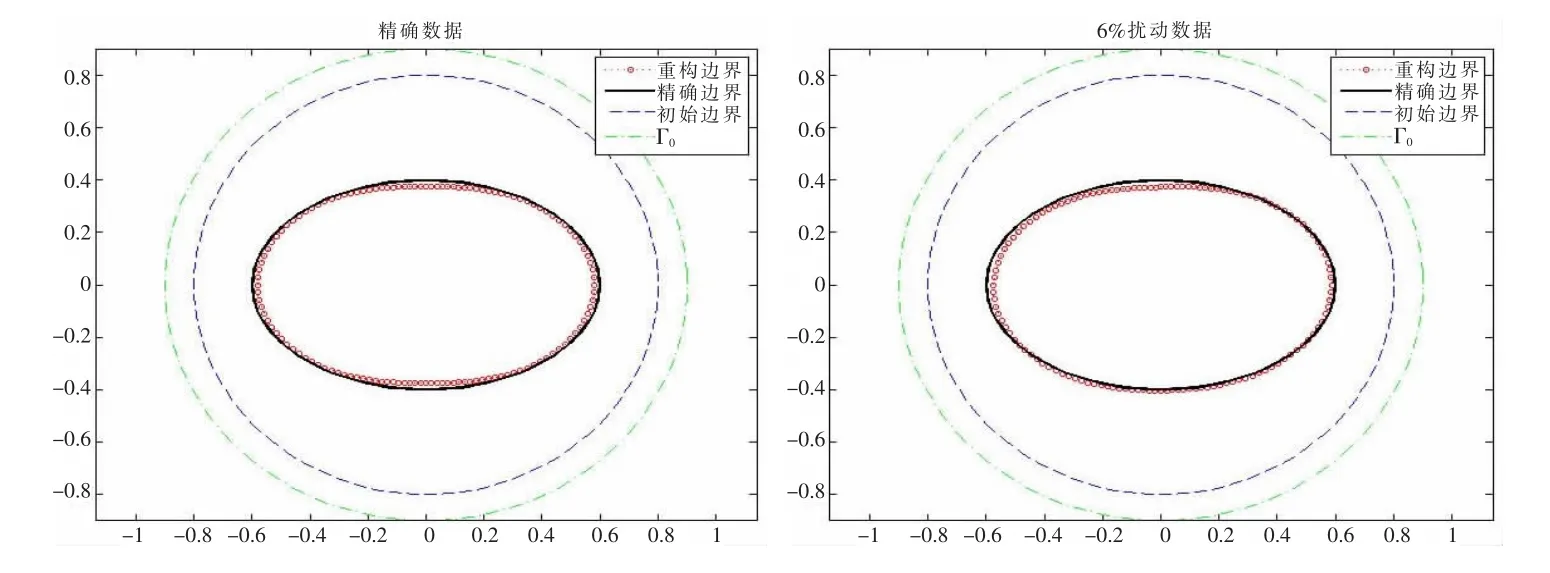
图2 用精确测量数据和6%扰动数据重构椭圆边界形状

图2中左图选取的正则化参数为αγ=10－2，αζ=10－1，迭代步数it=9。图2中右图选取的正则化参数为 αγ=10－2，αζ=10－2，迭代步数 it=7。

例2:考虑梨边界，其参数化形式为

给定Dirichlet数据 f(z0(t))=1，Γ1上的阻尼系数为，同样用精确数据和扰动数据可以得到图3所示的结果。

图3 用精确测量数据和3%扰动数据重构梨边界形状

图3中2个图选取的正则化参数均为αγ=9×10－1，αζ=10－2，迭代步数 it=6。考虑对不同的Dirichlet数据f(z0(t))=1+sin2t重构梨边界形状，Γ1上的阻尼系数仍为=1+cos4t，得到图4所示的重构结果。

图4中2个图选取的正则化参数均为αγ=10－1，αζ=5 ×10－1，迭代步数 it=6。这个算例说明对边界Γ0上不同的柯西数据提出的正则化迭代算法仍然是有效的。

例3:考虑苹果边界，其参数化形式为

取定 Dirichlet数据 f(z0(t))=1+sin2t，Γ1上的阻尼系数为，得到图 5所示的重构结果。

图4 用精确测量数据和3%扰动数据重构梨边界形状

图5 用精确测量数据和3%扰动数据重构苹果边界形状

图5中左图选取的正则化参数为αγ=10－3，αζ=6 ×10－2，迭代步数 it=13。图 5 中右图选取的正则化参数为 αγ=10－3，αζ=10－3，迭代步数 it=15。

通过上述3个数值例子可以看出，本文提出的重构内部边界形状的非线性积分方程法是有效的，无论Γ1上取不同阻尼系数，还是Γ0上取不同的Dirichlet数据，该算法都能很好的重构内部边界形状，并且对数据误差是稳定的。

致谢:感谢导师刘继军教授在本文完成中的讨论和提出的有效建议。

[1] Haddar H，Joly P，Nguyen H M.Generalized impedance boundary conditions for scattering problems from strongly absorbing obstacles:the case of maxwell's equations[J].Math Models and Methods in Appl Sci，2008，18:1787－127.

[2] Bourgeois L，Chaulet N，Haddar H.Stable reconstruction of generalized impedance boundary conditions[J].Inverse Problems，2011，27:095002 －26.

[3] Cakoni F，Kress R.Integral equation methods for the inverse obstacle problem with generalized impedance boundary condition[J].Inverse Problems，2013，29:015005－19.

[4] Kress R，Rundell W.Nonlinear integral equations and the iterative solution for an inverse boundary value problem[J].Inverse Problems，2005，21:1207 －1223.

[5] Cakoni F，Kress R，Schuft C.Integral equations for shape and impedance reconstruction in cottosion detection[J].Inverse Problems，2010，26:095012 －24.

[6] Cakoni F，Kress R，Schuft C.Simultaneous reconstruction of shape and impedance in corrosion detection[J].Methods Appl Anal，2010，17:331 －462.

[7] Qin H H，Cakoni F.Nonlinear integral equations for shape reconstruction in the inverse interior scattering problem[J].Inverse Problems，2011，27:035005 － 17.

[8] Colton D，Kress R.Inverse Acoustic and ElEctromagnetic Scattering Theory[M].Berlin:Springer，1998.