计算机辅助教学在《数学建模》课程中的运用——赤峰学院《数学建模》教学心得体会

李玉叶，王晓英

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

计算机辅助教学在《数学建模》课程中的运用
——赤峰学院《数学建模》教学心得体会

李玉叶，王晓英

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

《数学建模》是一门综合利用数学知识和计算机技术解决实际问题应用性很强的课程，是培养学生综合素质特别是数学应用能力的重要途径.但该课程涉及的知识领域众多，并且所研究的问题都来源于实际比较复杂，在授课中如果采用传统的单一授课方式，会使学生感到枯燥，难于理解而失去学习的兴趣，很难达到良好的效果.为了提高教学效率，要寓教于乐，运用计算机辅助的多种教学手段：运用现代化教学手段，提高学生对知识的理解；利用图形结合，加强学生的直观认识，培养学生运用所学知识的能力；亲自建模、编程，课堂讲授，发展学生的应用意识，培养实践能力.通过这些计算机辅助手段的运用，使枯燥、难于理解、涉及面广的《数学建模》课程变得形象、直观、易接受，从而获得了良好的教学效果.

《数学建模》； 课堂教学；教学手段

数学建模是利用数学方法解决实际问题的一种活动，是把数学知识与客观实际问题联系起来的纽带.是培养学生综合素质特别是数学应用能力的重要途径.《数学建模》这门课的开设培养了学生的创新能力、想象力、洞察力、判断力等，从而有效地体现了数学教育对于学生能力培养的重要作用.但在授课过程中，由于该门课程所涉及的领域广泛，且所建模的问题几乎来源于实际，因此，大多数情况下，涉及众多理论及复杂的实际问题，从而使得该课程在某种程度上显得索然无味，比较枯燥，大学生正处于思维活跃期，专注力持续时间有限，故而容易产生厌倦情绪，传统的教学方法，很难保证让学生持续专注，达到预期的目的.为了提高

《数学建模》这门课的教学的效率，使学生乐于学习，更好的掌握所学的知识，在该门课程的授课过程中，我们要突破以讲授为主的传统的教学手段，通过计算机辅助教学，采用多种教学手段，比如数形结合，图形结合，动态切换，图文并茂等，可以形象直观的学到知识，产生深刻的印象，并获得良好的教学效果.

1 运用现代化教学手段，提高学生对所学知识的理解能力

现代化的教学手段包括录像、录音、幻灯、投影、多媒体课件等影像资料，把这些直观的、生动的运用到《数学建模》的课堂教学中，能有效地提高教学质量.

比如“数学规划模型”这一节内容，对于根据实际问题所建的数学模型，其变量有十几个甚至几十个之多；除此之外，还有一些其他的约束条件.如此一来，变量参数多，计算量庞大，过程繁琐，因此传统的计算方法（如手工运算）求解比较困难.但对于该规划问题的求解，如果采用LINGO软件，就非常简便.LINGO（Linear Interactive and General Optimizer即“交互式的线性和通用优化求解器”），它可以用于一些线性和非线性方程组的求解，也可以用于求解非线性规划等，功能十分强大，是求解优化模型的最佳选择.但学生对此软件并不熟悉甚至没有听说过，更别提使用了.因此，为了提高课堂教学效果，我们借助多媒体课件首先给同学们介绍一下LINGO软件的基本使用方法，然后选取不同实际事例，不同变量个数的数学规划模型进行讲解.

例如：在讲授“奶制品的生产与销售”这一节时我们建立规划模型如下：

这是一个六个变量的线性规划问题，用LINGO求解就比较方便，在LINGO下新建一个模型文件（即LINGO程序，一般以“LG4”为后缀名），书写形式如下：

将文件存储并命名后，选择菜单“LINGO︳Solve”执行，即可得到如下的解：

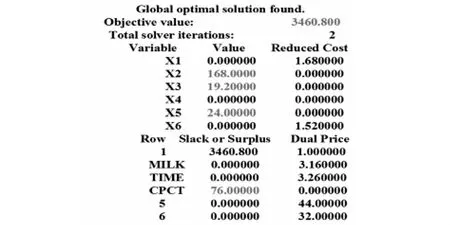
最优解为x1=0,x2=168,x3=19.2,x4=0,x5=24,x6=0,最优值为3460.8.通过计算机，可以轻松的改变变量，建立新的模型，从而更好地揭示规律.

2 利用图形结合，加强学生的直观认识，培养学生运用所学知识的能力

《数学建模》这门课程是近十几年来开设的一门新课程，它以现实问题为载体，把数学知识、数学软件和计算机应用有机的结合，融实用性、实践性、知识性和创造性于一体，特别强调学生的主体地位，在教师的指导下，用所学的数学知识和计算机技术，借助于数学软件，建立数学模型，分析、解决一些经过简化的现实问题.但是对于实际问题往往很复杂，建立的数学模型，无法通过求解数学方程得到其解析解，所以只能借助数学软件进行求解，将求得的数值解，用软件画图，以图的形式展现给学生，这样加强学生的直观认识，培养学生运用所学知识的能力.

例如，在讲授传染病模型SIR模型：

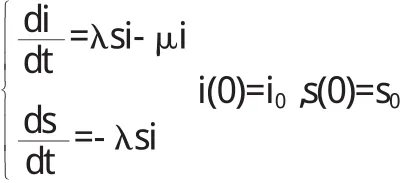
该方程无法求出s(t)和i(t)的解析解，我们只好求数值解，这就的借助于计算机软件，我们通过多媒体课件展示数值求解的程序，如下：

图1 s(t)和i(t)关于时间t的图

图2 i：s图形

3 亲自建模、编程，课堂讲授，发展学生的应用意识，培养实践能力

《数学建模》这门课程不是为了建模而建模,开设数学建模课的目的是通过建模加深学生对数学知识的理解,掌握建模的思想方法,促进其他课程的教学,提高学生的综合素质.因此在数学建模实践课中，要充分发挥学生的主体作用，充分调动学生的主观能动性，让学生们结合学习生活中所遇到的问题，进行选题，建模，编程求解、回答原问题等，学生完成以上工作后，进行课堂讲授、讨论，通过大家的不同建议及意见，作进一步的修正，同时，在这一过程中，对于学生，老师是一个引导者，启发者；而对于老师也是学习的过程，学习学生对这个问题的理解和认识；达到教学相长的相互有益的结果.在整个过程中，学生们要解决问题，必须善于深入地思考问题,迅速准确地把握问题的关键,揭开问题的本质,将现实问题抽象的化简为数学问题,搞清楚问题的已知条件、未知条件和求解目标，并找出以上因素之间的联系，建立模型.这个过程对于学生思维的深刻性和敏捷性得到了充分的锻炼.由于学生所作的建模问题是一个没有现成答案、模式的问题，所以他们在建立数学模型的过程中,充满了大量的分析与综合、猜侧与尝试、类比与联想等的创造性活动,这就需要学生充分发挥想象力和洞察力,创造性地去解决问题.而且数学建模所得结果只是最优解答,并非唯一解答,这样就给学生营造了一个可以充分发挥创造才能的空间.在完成了模型的建立、模型还得求解,实际问题抽象的数学模型往往很复杂，这就需要同学们自己编程借助软件求解，提高了学生利用计算机处理问题的能力.将所得的计算结果学生必须“翻译”回到现实问题中去,进行分析和检验.这是一个回顾和反思的过程，对于培养和训练学生思维的批判性具有十分重要的作用.

总之，通过该学期计算机教学的课堂效果显示，计算机辅助教学在数学建模课程中的作用是显而易见的，同学们的课堂积极性，知识收获程度，较上学期相比，有了很大的提升.通过计算机辅助的多种教学手段的运用，使枯燥、抽象、复杂的《数学建模》课程变得形象、直观，也提高了同学们的学习兴趣，从而获得了良好的教学效果.

〔1〕姜启源.数学模型[M].北京：高等教育出版社,1993.

〔2〕胡玉梅.高师院校数学建模课程建设的理论与实践研究[D].天津师范大学,2003.

〔3〕刘来福，杨淳，黄海洋.数学建模方法与分析[M].北京：机械工业出版社,2009.

〔4〕严士健.数学思维与数学意识、创新意识、应用意识[J].教学与教材研究，1999.

G642

A

1673-260X（2014）10-0003-02

内蒙古自治区自然科学基金面上项目（2012MS0103）资助